Generalized linear model and nonlinear regression model

Download this R markdown as: R, Rmd.

Outline of this lab session:

Generalized linear model
Nonlinear regression model

In normal linear model we assume that the continuous response variable \(Y \in \mathbb{R}\) has given \(p\)-variate covariates \(\mathbf{X} \in \mathbb{R}^p\) the following normal distribution \[ Y | \mathbf{X} \sim \mathsf{N}(\mathbf{X}^\top\boldsymbol{\beta}, \sigma^2), \] where \(\boldsymbol{\beta} \in \mathbb{R}^p\) is the unknown parameter vector and \(\sigma^2 > 0\) is (usually) the unknown variance parameter. The normality assumption is not strictly needed here (exact vs. asymptotic results and inference).

In the general linear regression model, the assumption about the homoscedastic variance is relaxed and the underlying model for the observed data \(\boldsymbol{Y} = (Y_1, \dots, Y_n)^\top\) given the corresponding model matrix \(\mathbb{X} \in \mathbb{R}^{n \times p }\) can be expressed as

\[ \boldsymbol{Y} | \mathbb{X} \sim \mathsf{N}_n(\mathbb{X} \boldsymbol{\beta}, \sigma^2\mathbb{W}^{-1}), \] for some general (positive definite) variance matrix \(\mathbb{W}^{-1}\). Again, the normality assumption in the model above can be omitted.

The concept of a linear model will be further generalized today.

1. Generalized linear model

Firstly, the generalized linear regression model is assumed, where the response variable \(Y\) does not follow the normal distribution any more (either continuous substantially different from normal or even discrete). The conditional expectation of \(Y\) given some vector of the subject specific covariates \(\mathbf{X}\) is modeled using an additional (nonlinear link function) that connects the linear predictor \(\mathbf{X}^\top\boldsymbol{\beta} \in \mathbb{R}\) with the conditional expectation \(\mu_x = \mathsf{E}[Y | \mathbf{X}] \in \mathcal{M} \subseteq \mathbb{R}\).

Typically, the model is assumed in a form \[ \mathsf{E}[Y | \mathbf{X}] = g^{-1}(\mathbf{X}^\top\boldsymbol{\beta}), \] where \(g(\cdot)\) is the so-called link function. Its purpose is to map the conditional expectation from \(\mathcal{M}\) onto the whole real line \(\mathbb{R}\) where the predictor lives.

Different models for different distributions of \(Y\) and different link functions \(g(\cdot)\) can be assumed and different statistical properties with different interpretation of the unknown vector of the parameters \(\boldsymbol{\beta} \in \mathbb{R}^p\) follow accordingly.

For illustration purposes we will consider the dataset mtcars and we will model the consumption of the car given some additional covariates.

data(mtcars)
mtcars$mpg01 <- as.numeric(mtcars$mpg > 20)
mtcars$fam <- factor(mtcars$am, levels = 0:1, labels = c("Automatic", "Manual"))
summary(mtcars)

##       mpg            cyl            disp             hp             drat            wt            qsec     
##  Min.   :10.4   Min.   :4.00   Min.   : 71.1   Min.   : 52.0   Min.   :2.76   Min.   :1.51   Min.   :14.5  
##  1st Qu.:15.4   1st Qu.:4.00   1st Qu.:120.8   1st Qu.: 96.5   1st Qu.:3.08   1st Qu.:2.58   1st Qu.:16.9  
##  Median :19.2   Median :6.00   Median :196.3   Median :123.0   Median :3.69   Median :3.33   Median :17.7  
##  Mean   :20.1   Mean   :6.19   Mean   :230.7   Mean   :146.7   Mean   :3.60   Mean   :3.22   Mean   :17.8  
##  3rd Qu.:22.8   3rd Qu.:8.00   3rd Qu.:326.0   3rd Qu.:180.0   3rd Qu.:3.92   3rd Qu.:3.61   3rd Qu.:18.9  
##  Max.   :33.9   Max.   :8.00   Max.   :472.0   Max.   :335.0   Max.   :4.93   Max.   :5.42   Max.   :22.9  
##        vs              am             gear           carb          mpg01              fam    
##  Min.   :0.000   Min.   :0.000   Min.   :3.00   Min.   :1.00   Min.   :0.000   Automatic:19  
##  1st Qu.:0.000   1st Qu.:0.000   1st Qu.:3.00   1st Qu.:2.00   1st Qu.:0.000   Manual   :13  
##  Median :0.000   Median :0.000   Median :4.00   Median :2.00   Median :0.000                 
##  Mean   :0.438   Mean   :0.406   Mean   :3.69   Mean   :2.81   Mean   :0.438                 
##  3rd Qu.:1.000   3rd Qu.:1.000   3rd Qu.:4.00   3rd Qu.:4.00   3rd Qu.:1.000                 
##  Max.   :1.000   Max.   :1.000   Max.   :5.00   Max.   :8.00   Max.   :1.000

In the following we will fit different models and we will compare the outputs. We start with ordinary linear model:

m <- list()
m[["lm"]] <- lm(mpg ~ disp + fam, data = mtcars)
summary(m[["lm"]])

## 
## Call:
## lm(formula = mpg ~ disp + fam, data = mtcars)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -4.638 -2.475 -0.563  2.233  6.839 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 27.84808    1.83407   15.18  2.5e-15 ***
## disp        -0.03685    0.00578   -6.37  5.7e-07 ***
## famManual    1.83346    1.43610    1.28     0.21    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.22 on 29 degrees of freedom
## Multiple R-squared:  0.733,  Adjusted R-squared:  0.715 
## F-statistic: 39.9 on 2 and 29 DF,  p-value: 4.75e-09

Generalized linear model with the identity link:

m[["glm-N-id"]] <- glm(mpg ~ disp + fam, data = mtcars) # family = gaussian(link = "identity")
summary(m[["glm-N-id"]])

## 
## Call:
## glm(formula = mpg ~ disp + fam, data = mtcars)
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 27.84808    1.83407   15.18  2.5e-15 ***
## disp        -0.03685    0.00578   -6.37  5.7e-07 ***
## famManual    1.83346    1.43610    1.28     0.21    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 10.35)
## 
##     Null deviance: 1126.05  on 31  degrees of freedom
## Residual deviance:  300.28  on 29  degrees of freedom
## AIC: 170.5
## 
## Number of Fisher Scoring iterations: 2

Generalized linear model with the inverse link:

m[["glm-N-inv"]] <- glm(mpg ~ disp + fam, data = mtcars, family = gaussian(link = "inverse"))
summary(m[["glm-N-inv"]])

## 
## Call:
## glm(formula = mpg ~ disp + fam, family = gaussian(link = "inverse"), 
##     data = mtcars)
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.74e-02   3.87e-03    7.08  8.7e-08 ***
## disp         1.20e-04   1.64e-05    7.31  4.7e-08 ***
## famManual   -2.31e-03   2.76e-03   -0.84     0.41    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 7.054)
## 
##     Null deviance: 1126.05  on 31  degrees of freedom
## Residual deviance:  204.55  on 29  degrees of freedom
## AIC: 158.2
## 
## Number of Fisher Scoring iterations: 6

Generalized linear model for the binary response with logit link - logistic regression:

m[["glm-bin-logit"]] <- glm(mpg01 ~ disp + fam, data = mtcars, family = binomial) # link = "logit"
summary(m[["glm-bin-logit"]])

## 
## Call:
## glm(formula = mpg01 ~ disp + fam, family = binomial, data = mtcars)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)  
## (Intercept)   5.1245     2.3231    2.21    0.027 *
## disp         -0.0287     0.0116   -2.47    0.013 *
## famManual     0.6141     1.4011    0.44    0.661  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 43.860  on 31  degrees of freedom
## Residual deviance: 16.381  on 29  degrees of freedom
## AIC: 22.38
## 
## Number of Fisher Scoring iterations: 7

Generalized linear model for the binary response with probit link - probit regression:

m[["glm-bin-probit"]] <- glm(mpg01 ~ disp + fam, data = mtcars, family = binomial(link = "probit"))
summary(m[["glm-bin-probit"]])

## 
## Call:
## glm(formula = mpg01 ~ disp + fam, family = binomial(link = "probit"), 
##     data = mtcars)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)   
## (Intercept)  3.03399    1.25320    2.42   0.0155 * 
## disp        -0.01656    0.00588   -2.82   0.0048 **
## famManual    0.30227    0.78331    0.39   0.6996   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 43.860  on 31  degrees of freedom
## Residual deviance: 16.155  on 29  degrees of freedom
## AIC: 22.15
## 
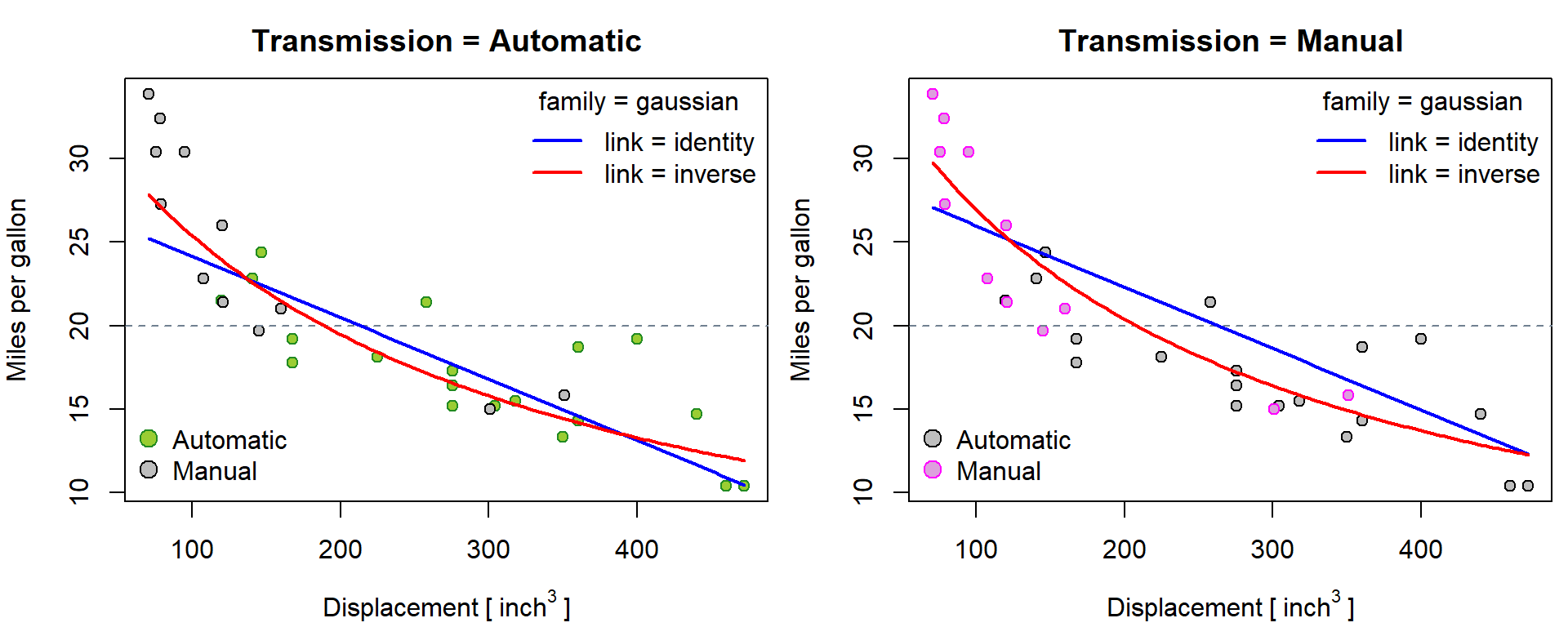
## Number of Fisher Scoring iterations: 8

Predictions based on glm class of models depend on family, link and purpose. We start with family = gaussian(...):

newdata <- list()
for(f in levels(mtcars$fam)){
  newdata[[f]] <- data.frame(disp = seq(min(mtcars$disp), max(mtcars$disp), length.out = 101),
                             fam = f)
}
BGf <- c("yellowgreen", "plum")
COLf <- c("forestgreen", "magenta")
names(COLf) <- names(BGf) <- levels(mtcars$fam)

par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
for(f in levels(mtcars$fam)){
  plot(mpg ~ disp, data = mtcars, 
       xlab = expression(Displacement~"["~inch^3~"]"), ylab = "Miles per gallon", 
       main = paste0("Transmission = ", f),
       pch = 21, col = ifelse(mtcars$fam==f, COLf[f], "black"), bg = ifelse(mtcars$fam==f, BGf[f], "grey"))
  abline(h = 20, col = "slategrey", lty = 2)
  lines(x = newdata[[f]]$disp, y = predict(m[["glm-N-id"]], newdata[[f]], type = "response"),
        col = "blue", lty = 1, lwd = 2)
  lines(x = newdata[[f]]$disp, y = predict(m[["glm-N-inv"]], newdata[[f]], type = "response"),
        col = "red", lty = 1, lwd = 2)
  legend("topright", c("link = identity", "link = inverse"), bty = "n",
         title = "family = gaussian", col = c("blue", "red"), lwd = 2)
  legend("bottomleft", levels(mtcars$fam), bty = "n",
         pt.bg = ifelse(levels(mtcars$fam)==f, BGf[f], "grey"),
         col = ifelse(levels(mtcars$fam)==f, COLf[f], "black"),
         pch = 21, pt.cex = 1.5)
}

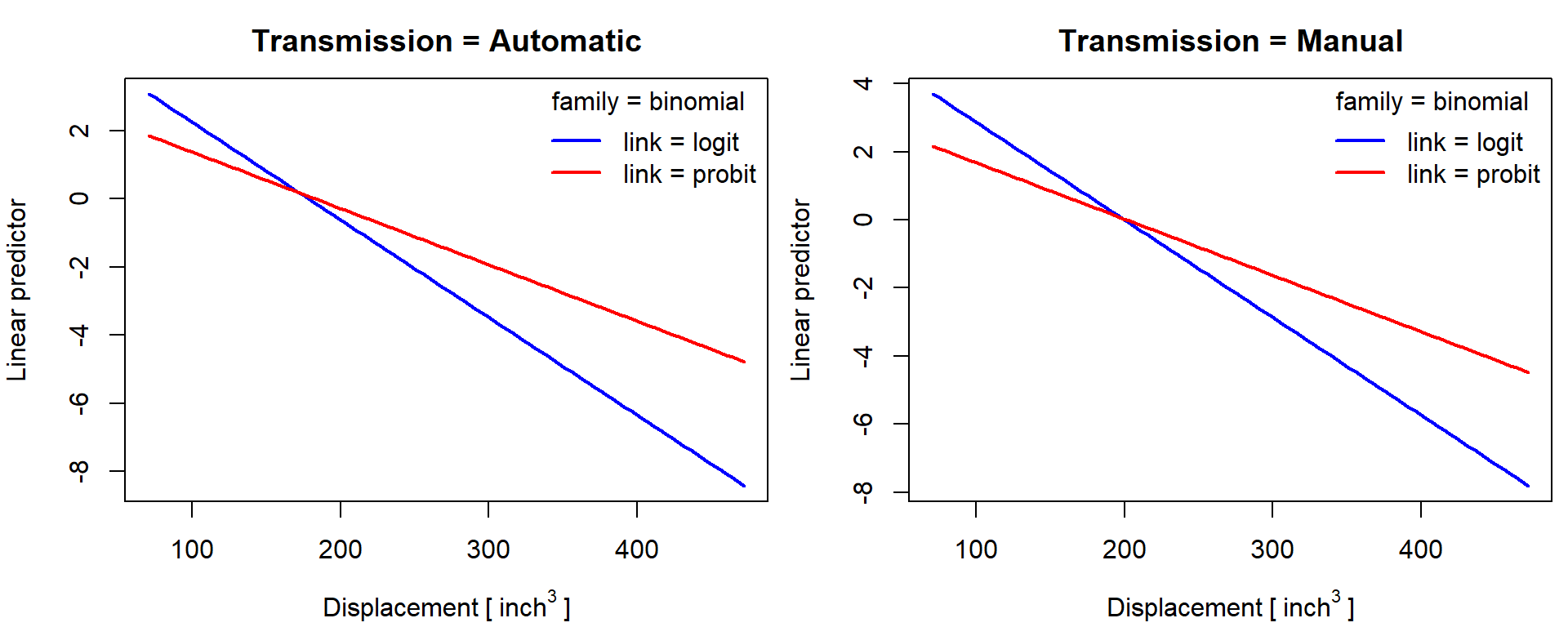
Linear predictor for binary mpg01 = mpg > 20 - predict type="link":

par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
for(f in levels(mtcars$fam)){
  plogit <- predict(m[["glm-bin-logit"]], newdata[[f]], type = "link")
  pprobit <- predict(m[["glm-bin-probit"]], newdata[[f]], type = "link")
  plot(plogit ~ newdata[[f]]$disp, type = "l",
       xlab = expression(Displacement~"["~inch^3~"]"), ylab = "Linear predictor", 
       ylim = range(plogit, pprobit),
       main = paste0("Transmission = ", f),
       col = "blue", lty = 1, lwd = 2)
  lines(pprobit ~ newdata[[f]]$disp, col = "red", lty = 1, lwd = 2)
  legend("topright", c("link = logit", "link = probit"), bty = "n",
         title = "family = binomial", col = c("blue", "red"), lwd = 2)
}

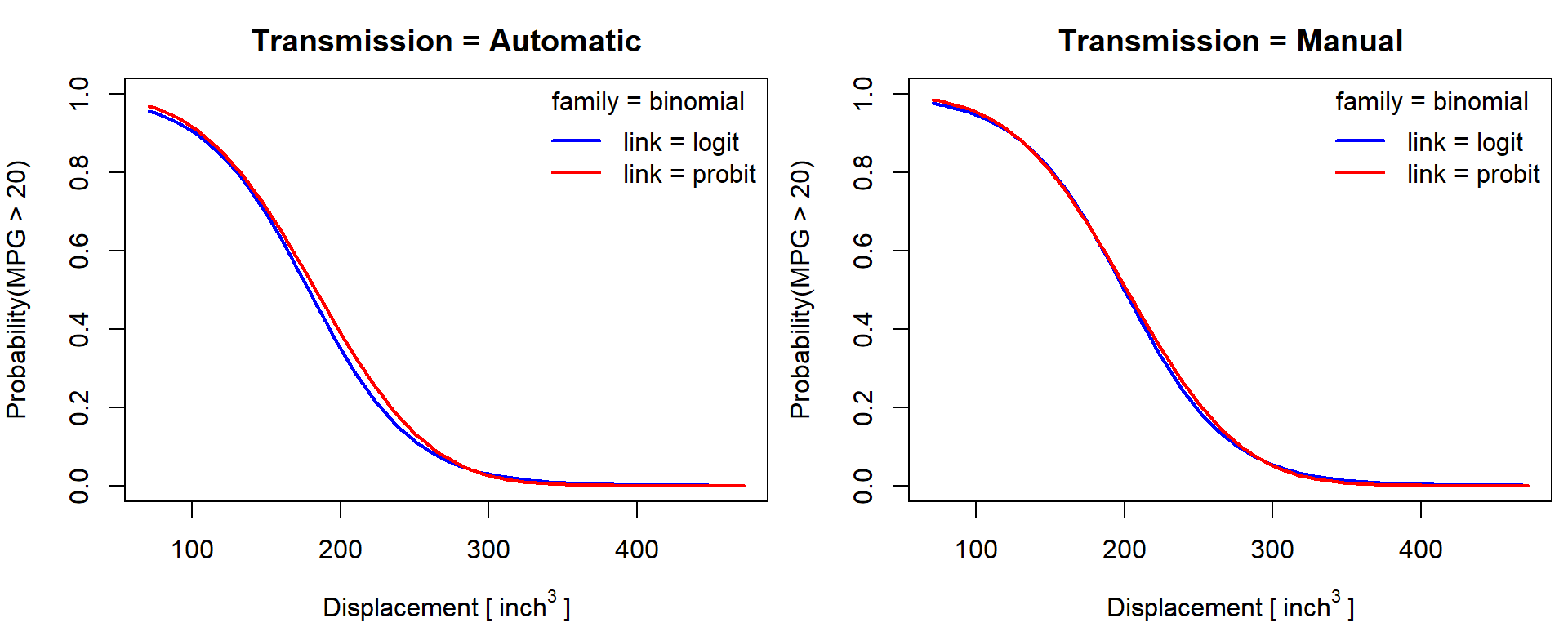
Estimated probability of mpg01 = mpg > 20 - predict type="response":

par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
for(f in levels(mtcars$fam)){
  plogit <- predict(m[["glm-bin-logit"]], newdata[[f]], type = "response")
  pprobit <- predict(m[["glm-bin-probit"]], newdata[[f]], type = "response")
  plot(plogit ~ newdata[[f]]$disp, type = "l",
       xlab = expression(Displacement~"["~inch^3~"]"), ylab = "Probability(MPG > 20)", 
       ylim = c(0,1),
       main = paste0("Transmission = ", f),
       col = "blue", lty = 1, lwd = 2)
  lines(pprobit ~ newdata[[f]]$disp, col = "red", lty = 1, lwd = 2)
  legend("topright", c("link = logit", "link = probit"), bty = "n",
         title = "family = binomial", col = c("blue", "red"), lwd = 2)
}

Individual work

Discuss and compare the models above. Which ones can be compared directly? Can you explain the differences that you observe?
What is the corresponding interpretation of all the parameters being estimated in the models above?
What are the conclusions between the model with the continuous response mpg and its dichotomous version mpg01?
Which of the estimated parameters in the three models above can you reconstruct manually?

2. Nonlinear regression model

The second generalization of the linear regression model involves the change of the linear predictor \(\boldsymbol{X}^\top\boldsymbol{\beta}\) into a nonlinear predictor \(f(\boldsymbol{X}, \boldsymbol{\beta})\), for some well-specified regression function \(f: \mathbb{R}^{p \times q} \to \mathcal{M}\) (with an analytic formula that depends on the parameter vector \(\boldsymbol{\beta} \in \mathbb{R}^q\)).

Nonlinear regression models in R can be fitted by using the command nls() (nonlinear least squares) – see the corresponding help session for more details (?nls).

Compare the following two models:

ordinary linear model:

m[["lm"]] <- lm(mpg ~ disp + am, data = mtcars)
summary(m[["lm"]])

## 
## Call:
## lm(formula = mpg ~ disp + am, data = mtcars)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -4.638 -2.475 -0.563  2.233  6.839 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 27.84808    1.83407   15.18  2.5e-15 ***
## disp        -0.03685    0.00578   -6.37  5.7e-07 ***
## am           1.83346    1.43610    1.28     0.21    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.22 on 29 degrees of freedom
## Multiple R-squared:  0.733,  Adjusted R-squared:  0.715 
## F-statistic: 39.9 on 2 and 29 DF,  p-value: 4.75e-09

linear model as nonlinear least squares:

start <- list()
start[["nls-as-lm"]] <- c(a = 0, b = 0, c = 0)
m[["nls-as-lm"]] <- nls(mpg ~ a + b * disp + c * am, data = mtcars, start[["nls-as-lm"]])
summary(m[["nls-as-lm"]])

## 
## Formula: mpg ~ a + b * disp + c * am
## 
## Parameters:
##   Estimate Std. Error t value Pr(>|t|)    
## a 27.84808    1.83407   15.18  2.5e-15 ***
## b -0.03685    0.00578   -6.37  5.7e-07 ***
## c  1.83346    1.43610    1.28     0.21    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.22 on 29 degrees of freedom
## 
## Number of iterations to convergence: 1 
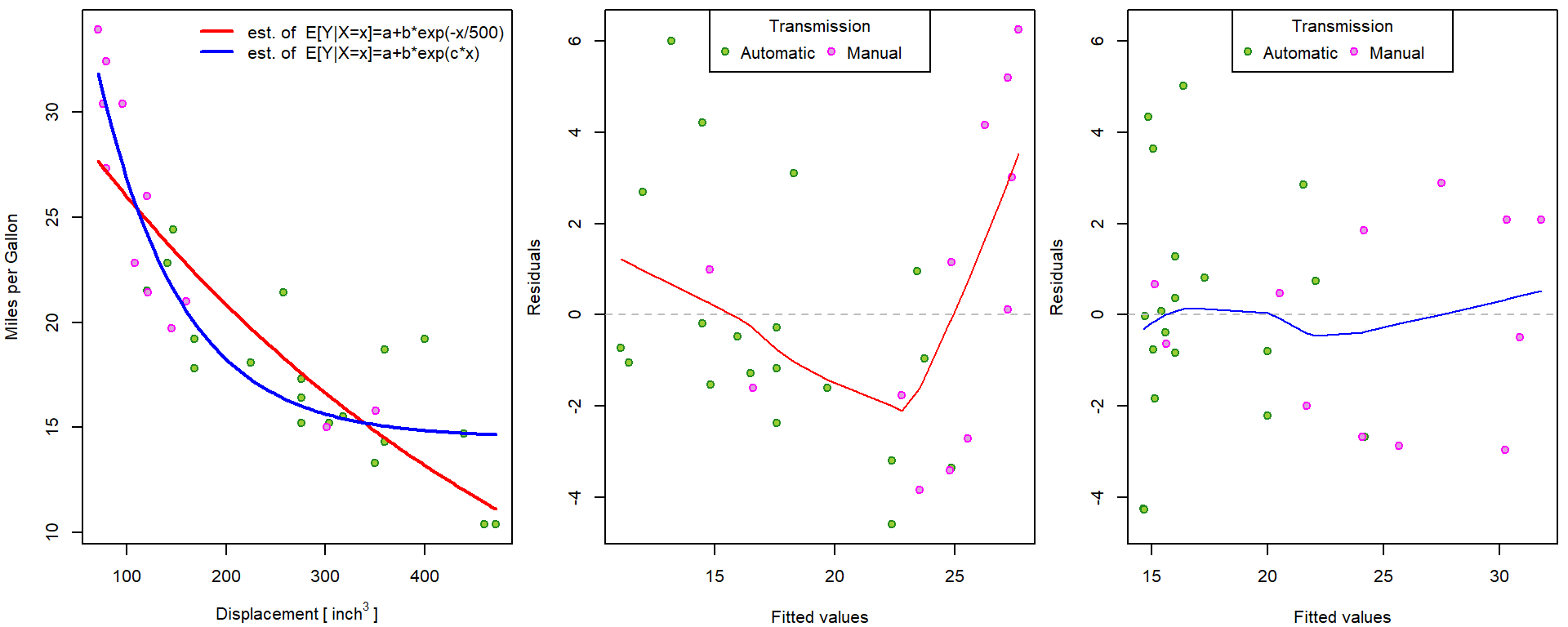
## Achieved convergence tolerance: 3.55e-09

Consider some nonlinear model that will properly fit the scatterplot of the data below:

par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, 
     xlab = expression(Displacement~"["~inch^3~"]"), ylab = "Miles per Gallon", 
     pch = 21, bg = BGf[fam], col = COLf[fam])
legend("topright", legend = levels(mtcars$fam), bty = "n",
       pch = 21, pt.bg = BGf, col = COLf)

For instance, exponential function could be reasonable. Using linear regression we would be able to only fit the following model with fixed choice of constant in exponent:

start[["nls-exp-1"]] <- c(a = 0, b = 0)
m[["nls-exp-1"]] <- nls(mpg ~ a + b * exp(-disp/500), data = mtcars, start[["nls-exp-1"]])
summary(m[["nls-exp-1"]])

## 
## Formula: mpg ~ a + b * exp(-disp/500)
## 
## Parameters:
##   Estimate Std. Error t value Pr(>|t|)    
## a    -2.33       2.35   -0.99     0.33    
## b    34.57       3.52    9.81  7.2e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.99 on 30 degrees of freedom
## 
## Number of iterations to convergence: 1 
## Achieved convergence tolerance: 1.23e-09

To find reasonable constant in exponent we can make it another model parameter:

# A successful run requires proper setting of initial values
a.0 <- min(mtcars$mpg) * 0.5
auxlm <- lm(log(mpg - a.0) ~ disp, data=mtcars)
start[["nls-exp-2"]] <- c(a.0, exp(coef(auxlm)[1]), coef(auxlm)[2])
names(start[["nls-exp-2"]]) <- letters[1:3]
# end of finding reasonable starting values 
m[["nls-exp-2"]] <- nls(mpg ~ a + b * exp(c * disp), data = mtcars, start[["nls-exp-2"]])
summary(m[["nls-exp-2"]])

## 
## Formula: mpg ~ a + b * exp(c * disp)
## 
## Parameters:
##   Estimate Std. Error t value Pr(>|t|)    
## a 14.50544    0.94383   15.37  1.8e-15 ***
## b 40.26532    7.94320    5.07  2.1e-05 ***
## c -0.01188    0.00247   -4.81  4.3e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.44 on 29 degrees of freedom
## 
## Number of iterations to convergence: 11 
## Achieved convergence tolerance: 5.72e-06

The model can be fitted into the data as follows:

pred <- list()
xgrid <- seq(min(mtcars$disp), max(mtcars$disp), length = 101)
pred_manual <- coef(m[["nls-exp-1"]])[1] + coef(m[["nls-exp-1"]])[2] * exp(- xgrid/500)
pred[["nls-exp-1"]] <- predict(m[["nls-exp-1"]], newdata = data.frame(disp = xgrid))
all.equal(pred[["nls-exp-1"]], pred_manual)

## [1] TRUE

pred[["nls-exp-2"]] <- predict(m[["nls-exp-2"]], newdata = data.frame(disp = xgrid))

COLm <- c("red", "blue")
names(COLm) <- c("nls-exp-1", "nls-exp-2")

par(mfrow = c(1,3), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, 
     xlab = expression(Displacement~"["~inch^3~"]"), ylab = "Miles per Gallon", 
     pch = 21, bg = BGf[fam], col = COLf[fam])
for(model in c("nls-exp-1", "nls-exp-2")){
  lines(pred[[model]] ~ xgrid, col = COLm[model], lwd = 2)
}
legend("topright", bty = "n", 
       legend = c("est. of  E[Y|X=x]=a+b*exp(-x/500)",
                  "est. of  E[Y|X=x]=a+b*exp(c*x)"),
       col = COLm, lwd = 2, lty = 1)

# residuals vs fitted - own implementation
res_fit <- function(m, YLIM = range(residuals(m))){
  plot(residuals(m) ~ fitted(m),
       xlab = "Fitted values", ylab = "Residuals", 
       ylim = YLIM, pch = 21, bg = BGf[mtcars$fam], col = COLf[mtcars$fam])
  abline(h=0, col = "grey", lty = 2)
  lines(lowess(residuals(m) ~ fitted(m)), col = COLm[model])
  legend("top", legend = levels(mtcars$fam), ncol = 2,
         title = "Transmission", pch = 21, pt.bg = BGf, col = COLf)
}
YLIM <- range(residuals(m[["nls-exp-1"]]), residuals(m[["nls-exp-2"]]))
for(model in c("nls-exp-1", "nls-exp-2")){
  res_fit(m[[model]], YLIM = YLIM)
}

How to include different exponential functions for different transmission?

model <- "nls-exp-by-am"
start[[model]] <- c(coef(m[["nls-exp-2"]]), rep(0, 3))
names(start[[model]]) <- letters[1:6]
m[[model]] <- nls(mpg ~ (a+d*am) + (b+e*am) * exp((c+f*am)*disp), data = mtcars, start[[model]])
summary(m[[model]])

## 
## Formula: mpg ~ (a + d * am) + (b + e * am) * exp((c + f * am) * disp)
## 
## Parameters:
##    Estimate Std. Error t value Pr(>|t|)  
## a -2.52e+01   2.32e+02   -0.11    0.914  
## b  5.11e+01   2.28e+02    0.22    0.824  
## c -6.52e-04   3.58e-03   -0.18    0.857  
## d  4.04e+01   2.32e+02    0.17    0.863  
## e -2.49e+00   2.28e+02   -0.01    0.991  
## f -1.38e-02   5.70e-03   -2.43    0.022 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.37 on 26 degrees of freedom
## 
## Number of iterations to convergence: 17 
## Achieved convergence tolerance: 6.56e-06

predy_aut <- predict(m[[model]], newdata = data.frame(disp = xgrid, am = 0))
predy_man <- predict(m[[model]], newdata = data.frame(disp = xgrid, am = 1))

par(mfrow = c(1,2), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, 
     xlab = expression(Displacement~"["~inch^3~"]"), ylab = "Miles per Gallon", 
     pch = 21, bg = BGf[fam], col = COLf[fam])
lines(predy_aut ~ xgrid, col = COLf["Automatic"], lwd = 2)
lines(predy_man ~ xgrid, col = COLf["Manual"], lwd = 2)
legend("topright", legend = levels(mtcars$fam), bty = "n",
       lty = 1, lwd = 2, col = COLf)

COLm[model] <- "red"
res_fit(m[[model]])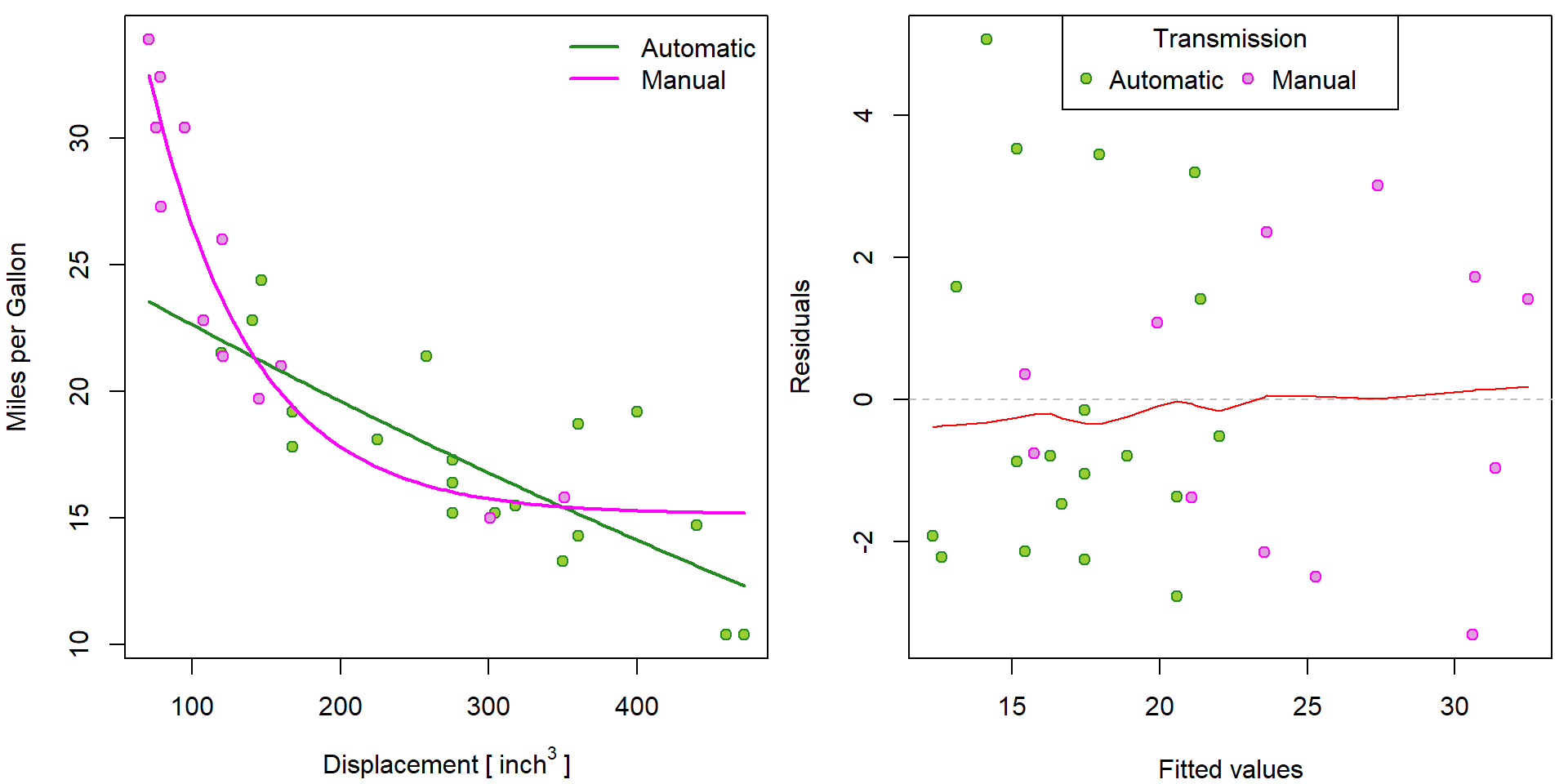

Individual work

Compare the model above with a standard linear regression model.
Design a formula that would have linear trend for Automatic and exponential trend for Manual.
Consider also models where the response mpg would be transformed by logarithm.

Generalized linear model and nonlinear regression model

Jan Vávra

Exercise 11

1. Generalized linear model

Individual work

2. Nonlinear regression model

Individual work