Statistical inference in a normal linear model
Jan Vávra
Exercise 8
Download this R markdown as: R, Rmd.
Outline of this lab session:
- Statistical inference in a normal linear model
- Confidence intervals, confidence regions, statistical tests
- Bounds around and for the linear regression line
- Prediction intervals
Loading the data and libraries
library("mffSM") # Dris data and LSest() function
library("car") # confidenceEllipse() functionWe will consider a simple linear regression model - modelling the
amount of yield given the information about the
concentration of magnesium Mg. For some model improvements
we will use the logarithm transformation of the independent covariate
(Mg).
data(Dris, package = "mffSM")
head(Dris)## yield N P K Ca Mg
## 1 5.47 470 47 320 47 11
## 2 5.63 530 48 357 60 16
## 3 5.63 530 48 310 63 16
## 4 4.84 482 47 357 47 13
## 5 4.84 506 48 294 52 15
## 6 4.21 500 45 283 61 14summary(Dris)## yield N P K Ca Mg
## Min. :1.92 Min. :268 Min. :32.0 Min. :200 Min. :29.0 Min. : 8.0
## 1st Qu.:4.04 1st Qu.:427 1st Qu.:43.0 1st Qu.:338 1st Qu.:41.8 1st Qu.:10.0
## Median :4.84 Median :473 Median :49.0 Median :377 Median :49.0 Median :11.0
## Mean :4.86 Mean :470 Mean :48.6 Mean :375 Mean :51.5 Mean :11.6
## 3rd Qu.:5.56 3rd Qu.:518 3rd Qu.:54.0 3rd Qu.:407 3rd Qu.:59.0 3rd Qu.:13.0
## Max. :8.79 Max. :657 Max. :72.0 Max. :580 Max. :95.0 Max. :22.0A simple linear model fitted in the last session
aLogMg <- lm(yield ~ log2(Mg), data = Dris)
summary(aLogMg) ##
## Call:
## lm(formula = yield ~ log2(Mg), data = Dris)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.119 -0.741 -0.074 0.745 3.984
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.485 0.779 1.91 0.057 .
## log2(Mg) 0.961 0.221 4.35 1.8e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.07 on 366 degrees of freedom
## Multiple R-squared: 0.0491, Adjusted R-squared: 0.0465
## F-statistic: 18.9 on 1 and 366 DF, p-value: 1.77e-05We will use the model above and we will construct:
- Point estimates of linear combinations of regression coefficients
and three different types of the confidence intervals/bounds for the model:
- Pointwise confidence intervals (region/band) AROUND the regression line
- Confidence region (band) FOR the (whole) regression line simultaneously
- Prediction interval (for some new given value of \(\boldsymbol{X}\))
0. Point estimates of the regression line
Firstly, use the help session in R to find out, what is the purpose
of the predict command? Try the following:
help(predict)
help(predict.lm)What is the difference between the outputs from “predict” and “fitted”? A few values are shown in the output below.
data.frame(Predict = predict(aLogMg), Fitted = fitted(aLogMg))[1:10,]## Predict Fitted
## 1 4.808 4.808
## 2 5.327 5.327
## 3 5.327 5.327
## 4 5.039 5.039
## 5 5.238 5.238
## 6 5.142 5.142
## 7 5.142 5.142
## 8 5.327 5.327
## 9 5.327 5.327
## 10 5.142 5.142all.equal(predict(aLogMg), fitted(aLogMg))## [1] TRUENow, we will use the same command, however, for some new value of \(X\) (concentration of magnesium)
predict(aLogMg, newdata = data.frame(Mg = 10))## 1
## 4.676(point.fit <- aLogMg$coef[1] + aLogMg$coef[2]*log2(10))## (Intercept)
## 4.676It can be even obtained with the corresponding standard error
predict(aLogMg, newdata = data.frame(Mg = 10), se.fit = TRUE)## $fit
## 1
## 4.676
##
## $se.fit
## [1] 0.07064
##
## $df
## [1] 366
##
## $residual.scale
## [1] 1.07The standard error can be also reconstructed manually
lvec <- c(1, log2(10))
(se.fit <- c(sqrt(t(lvec) %*% vcov(aLogMg) %*% lvec)))## [1] 0.07064all.equal(predict(aLogMg, newdata = data.frame(Mg = 10), se.fit = TRUE)$se.fit,
se.fit)## [1] TRUE# Recall - residual degrees of freedom, i.e. $df
aLogMg$df.residual## [1] 366# sqrt(MS_e) = estimate of sigma, i.e. $residual scale
sqrt(deviance(aLogMg)/aLogMg$df.residual)## [1] 1.07summary(aLogMg)$sigma## [1] 1.07Alternatively, the output can be also obtained from the
LSest() function in the R library mffSM:
LSest(aLogMg, L = c(1, log2(10)))## Estimate Std. Error t value P value Lower Upper
## 1 4.676 0.07064 66.19 <2e-16 4.537 4.815This function provides the outputs for any linear combination of
regression coefficients, which are in normal linear model based on \[
\dfrac{
l^\top \left( \widehat{\boldsymbol{\beta}} -
\boldsymbol{\beta}_0\right)
}{
\sqrt{\mathsf{MS}_e\; l^\top
\left(\mathbb{X}^\top\mathbb{X}\right)^{-1} l}
}
\sim \mathsf{T}_{n-p}.
\] In general, you can supply multiple linear combinations in
matrix L, where each row corresponds to one
combination.
1. Pointwise confidence intervals (region/band) AROUND the regression line
When we are interested in the estimate of the conditional mean \(E[Y | \boldsymbol{X} = \boldsymbol{x}]\) we can provide both the point estimate or the interval estimate. For the interval estimate, we need the confidence level and the estimate of the variance parameter.
It can be given automatically as follows;
predict(aLogMg, newdata = data.frame(Mg = 10), interval = "confidence", level = 0.95)## fit lwr upr
## 1 4.676 4.537 4.815Or, alternatively, we can reconstruct everything manually:
xt_beta <- as.numeric(crossprod(c(1, log2(10)), coef(aLogMg)))
xt_beta + c(-1, 1) * se.fit * qt(0.975, df = aLogMg[["df.residual"]])## [1] 4.537 4.815We can calculate a sequence of confidence intervals for \(E[Y | \boldsymbol{X} = \boldsymbol{x}]\) for different values of \(\boldsymbol{x}\)
predict(aLogMg, newdata = data.frame(Mg = 10:20), interval = "confidence", level = 0.95)## fit lwr upr
## 1 4.676 4.537 4.815
## 2 4.808 4.695 4.921
## 3 4.928 4.815 5.042
## 4 5.039 4.904 5.175
## 5 5.142 4.975 5.309
## 6 5.238 5.036 5.439
## 7 5.327 5.091 5.563
## 8 5.411 5.141 5.682
## 9 5.490 5.187 5.794
## 10 5.565 5.230 5.901
## 11 5.636 5.271 6.002predict(aLogMg, newdata = data.frame(Mg = 10:20), interval = "confidence", level = 0.95, se.fit = TRUE)## $fit
## fit lwr upr
## 1 4.676 4.537 4.815
## 2 4.808 4.695 4.921
## 3 4.928 4.815 5.042
## 4 5.039 4.904 5.175
## 5 5.142 4.975 5.309
## 6 5.238 5.036 5.439
## 7 5.327 5.091 5.563
## 8 5.411 5.141 5.682
## 9 5.490 5.187 5.794
## 10 5.565 5.230 5.901
## 11 5.636 5.271 6.002
##
## $se.fit
## 1 2 3 4 5 6 7 8 9 10 11
## 0.07064 0.05726 0.05768 0.06876 0.08476 0.10234 0.12011 0.13751 0.15433 0.17051 0.18603
##
## $df
## [1] 366
##
## $residual.scale
## [1] 1.07A denser grid of x-values to obtain the pointwise confidence band AROUND the regression line:
x.Mg <- seq(min(Dris[, "Mg"]) - 1, max(Dris[, "Mg"]) + 1, length = 101)
ciEY.aLogMg <- predict(aLogMg, data.frame(Mg = x.Mg), interval = "confidence",
level = 0.95)Observations together with the estimated regression line and a sequence of confidence intervals for \(E[Y|\boldsymbol{X} = \boldsymbol{x}]\) are visualized as a band – confidence region (band) AROUND the regression line.
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(yield ~ log2(Mg), data = Dris,
ylab = "Yield", xlab = "Log2(Mg)",
pch = 23, col = "orange", bg = "beige")
lines(log2(x.Mg), ciEY.aLogMg[, "fit"], lwd = 2, col = "red4")
lines(log2(x.Mg), ciEY.aLogMg[, "lwr"], lwd = 2, col = "red3", lty = 2)
lines(log2(x.Mg), ciEY.aLogMg[, "upr"], lwd = 2, col = "red3", lty = 2)
### Where is the band narrowest?
abline(v = mean(log2(Dris$Mg)))
abline(h = mean(Dris$yield))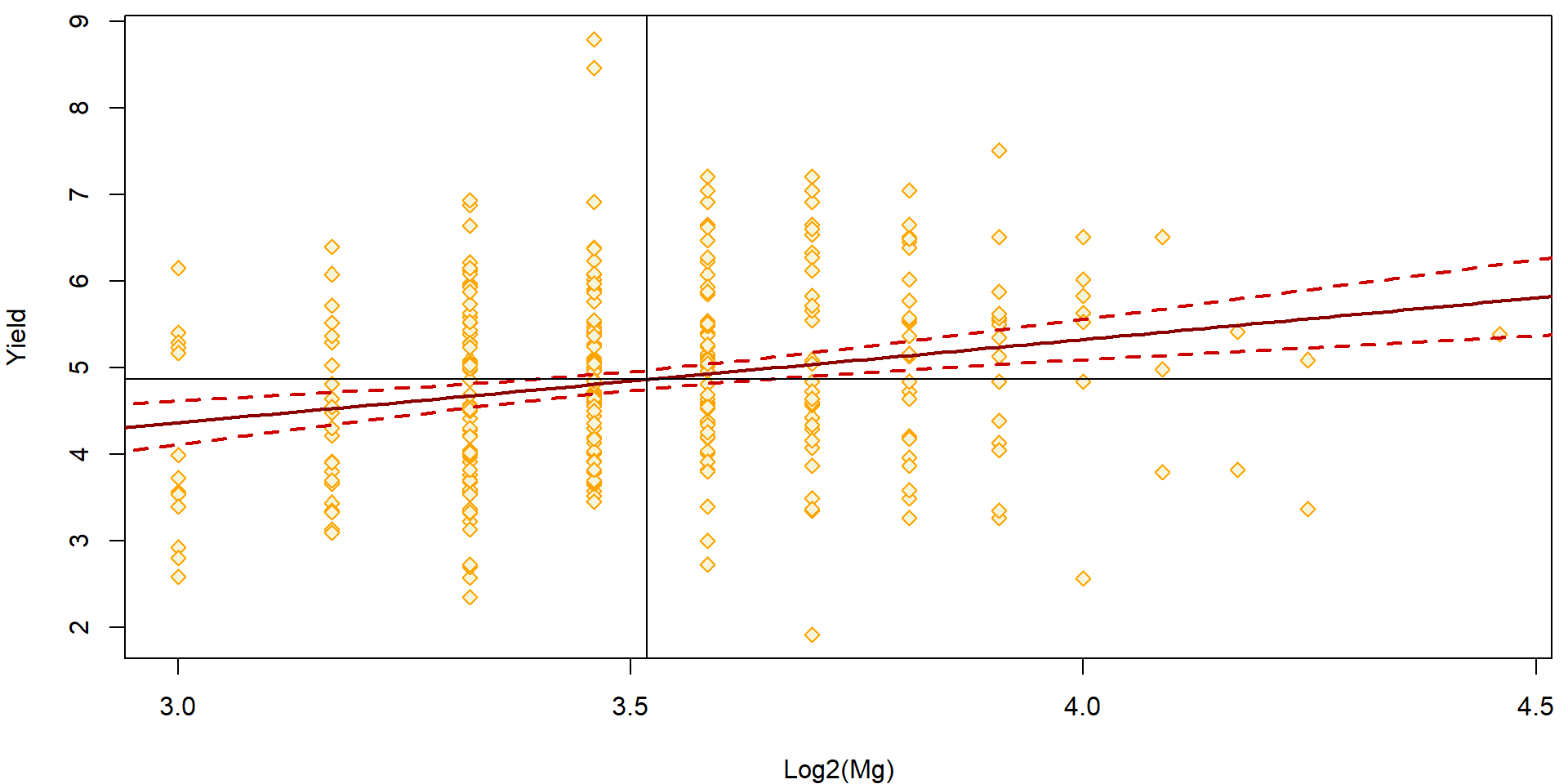
Everything can be also plotted with respect to the original scale of the magnesium concentration:
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(yield ~ Mg, data = Dris,
ylab = "Yield", xlab = "Mg",
pch = 23, col = "orange", bg = "beige")
lines(x.Mg, ciEY.aLogMg[, "fit"], lwd = 2, col = "red4")
lines(x.Mg, ciEY.aLogMg[, "lwr"], lwd = 2, col = "red3", lty = 2)
lines(x.Mg, ciEY.aLogMg[, "upr"], lwd = 2, col = "red3", lty = 2)
### What about now?
abline(v = 2^mean(log2(Dris$Mg)))
abline(h = mean(Dris$yield))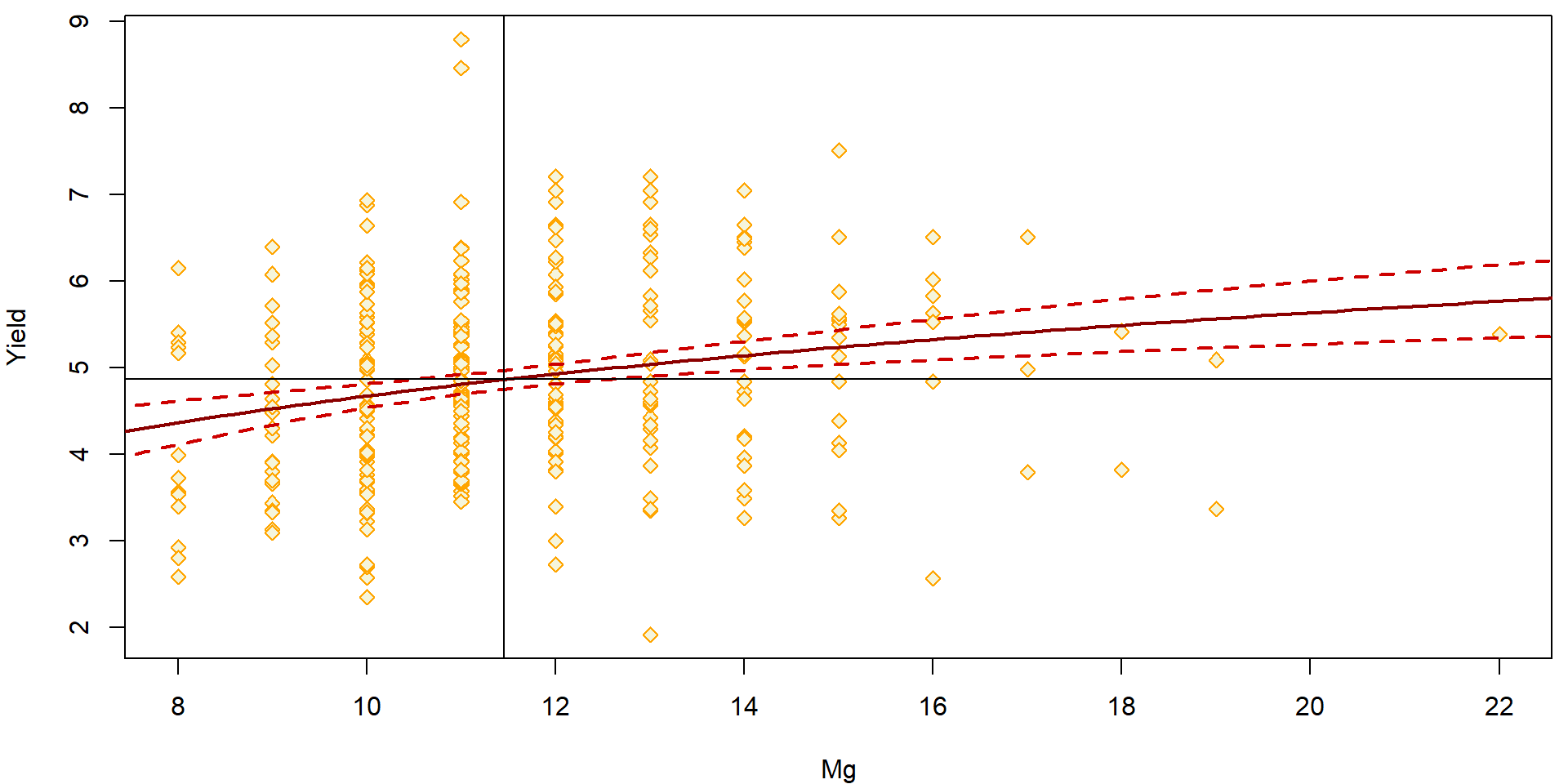
2. Confidence region (band) FOR the (whole) regression line simultaneously
The second option provides a confidence band for the whole regression line simultaneously. Note, that there is different interpretation of the point-wise band constructed above (where each interval can be interpreted only individually, for some some given value of the explanatory vector \(\boldsymbol{X} = \boldsymbol{x}\)).
Some theoretical details towards the band FOR the whole regression line simultaneously were given during the lecture, nevertheless, the code provided below can be considered as purely illustrative. It is only important to understand the difference between
- the point-wise band AROUND the regression line and
- the simultaneous band FOR the whole regression line at once.
ciEY2.aLogMg <- predict(aLogMg, data.frame(Mg = x.Mg), se.fit = TRUE)
forEY.aLogMg <- data.frame(
fit = ciEY2.aLogMg[["fit"]],
lwr = ciEY2.aLogMg[["fit"]] - ciEY2.aLogMg[["se.fit"]] * sqrt(qf(0.95, 2, ciEY2.aLogMg[["df"]])*2),
upr = ciEY2.aLogMg[["fit"]] + ciEY2.aLogMg[["se.fit"]] * sqrt(qf(0.95, 2, ciEY2.aLogMg[["df"]])*2))
head(forEY.aLogMg)## fit lwr upr
## 1 4.182 3.772 4.591
## 2 4.213 3.820 4.606
## 3 4.244 3.867 4.620
## 4 4.274 3.913 4.634
## 5 4.303 3.957 4.649
## 6 4.332 4.001 4.662The computation of the confidence band is based on the confidence ellipse for the regression parameters (\(\beta_0\), \(\beta_1\))
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
confidenceEllipse(aLogMg)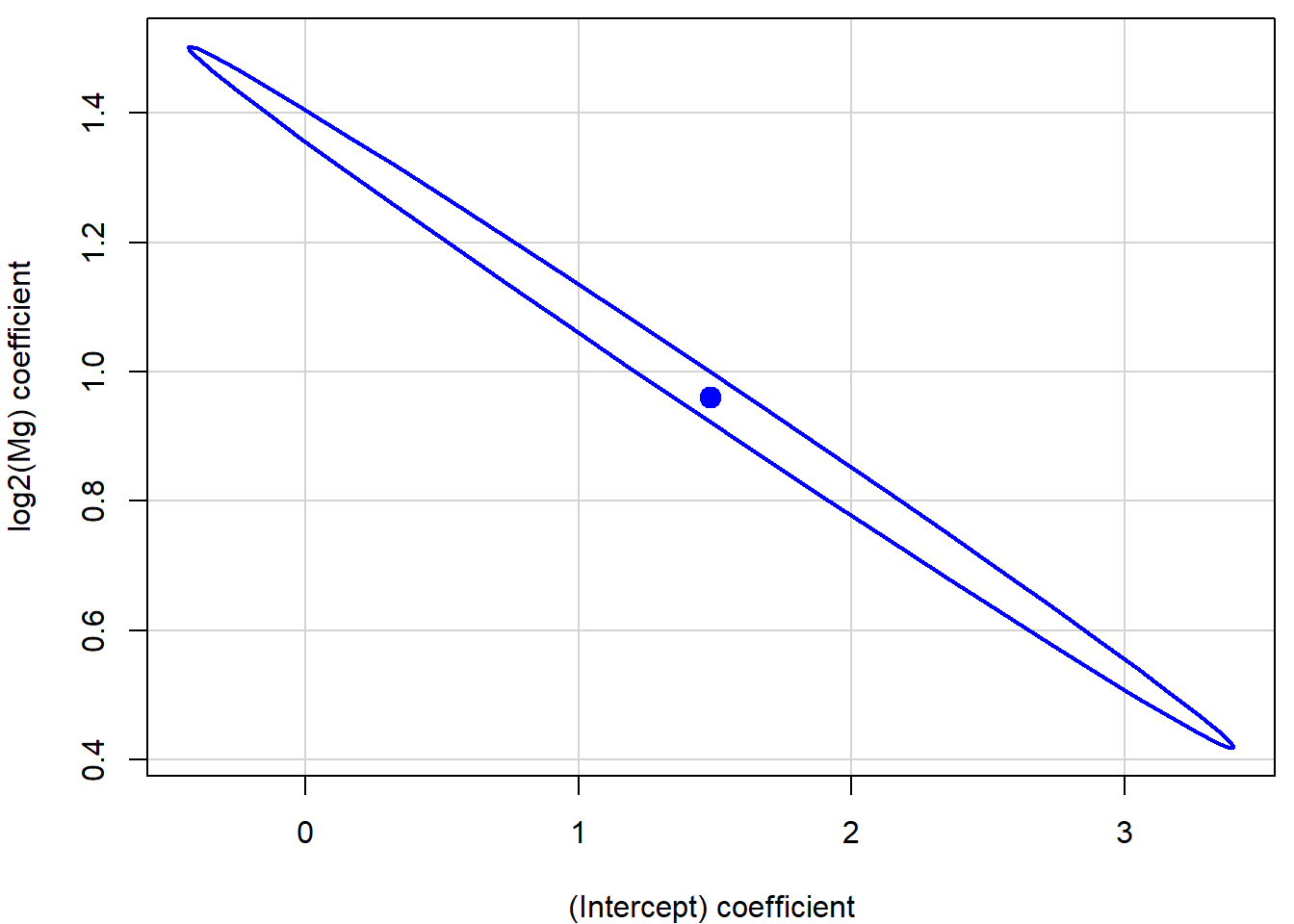
The regression lines can be visualized on the logarithm scale or the original scale of the logarithm concentration:
par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
## Log scale
plot(yield ~ log2(Mg), data = Dris,
ylab = "Yield", xlab = "Log2(Mg)", main = "Log scale",
pch = 23, col = "orange", bg = "beige")
lines(log2(x.Mg), ciEY.aLogMg[, "fit"], lwd = 2, col = "darkgreen")
# Band AROUND
lines(log2(x.Mg), ciEY.aLogMg[, "lwr"], lwd = 2, col = "red3", lty = 2)
lines(log2(x.Mg), ciEY.aLogMg[, "upr"], lwd = 2, col = "red3", lty = 2)
# Band FOR
lines(log2(x.Mg), forEY.aLogMg[, "lwr"], lwd = 2, col = "blue2", lty = 4)
lines(log2(x.Mg), forEY.aLogMg[, "upr"], lwd = 2, col = "blue2", lty = 4)
legend("topright", legend = c("For", "Around"), bty = "n",
col = c("blue2", "red3"), lty = c(4, 2), lwd = 2)
## Original scale
plot(yield ~ Mg, data = Dris,
ylab = "Yield", xlab = "Mg", main = "Original scale",
pch = 23, col = "orange", bg = "beige")
lines(x.Mg, ciEY.aLogMg[, "fit"], lwd = 2, col = "darkgreen")
# Band AROUND
lines(x.Mg, ciEY.aLogMg[, "lwr"], lwd = 2, col = "red3", lty = 2)
lines(x.Mg, ciEY.aLogMg[, "upr"], lwd = 2, col = "red3", lty = 2)
# Band FOR
lines(x.Mg, forEY.aLogMg[, "lwr"], lwd = 2, col = "blue2", lty = 4)
lines(x.Mg, forEY.aLogMg[, "upr"], lwd = 2, col = "blue2", lty = 4)
legend("topright", legend = c("For", "Around"), bty = "n",
col = c("blue2", "red3"), lty = c(4, 2), lwd = 2)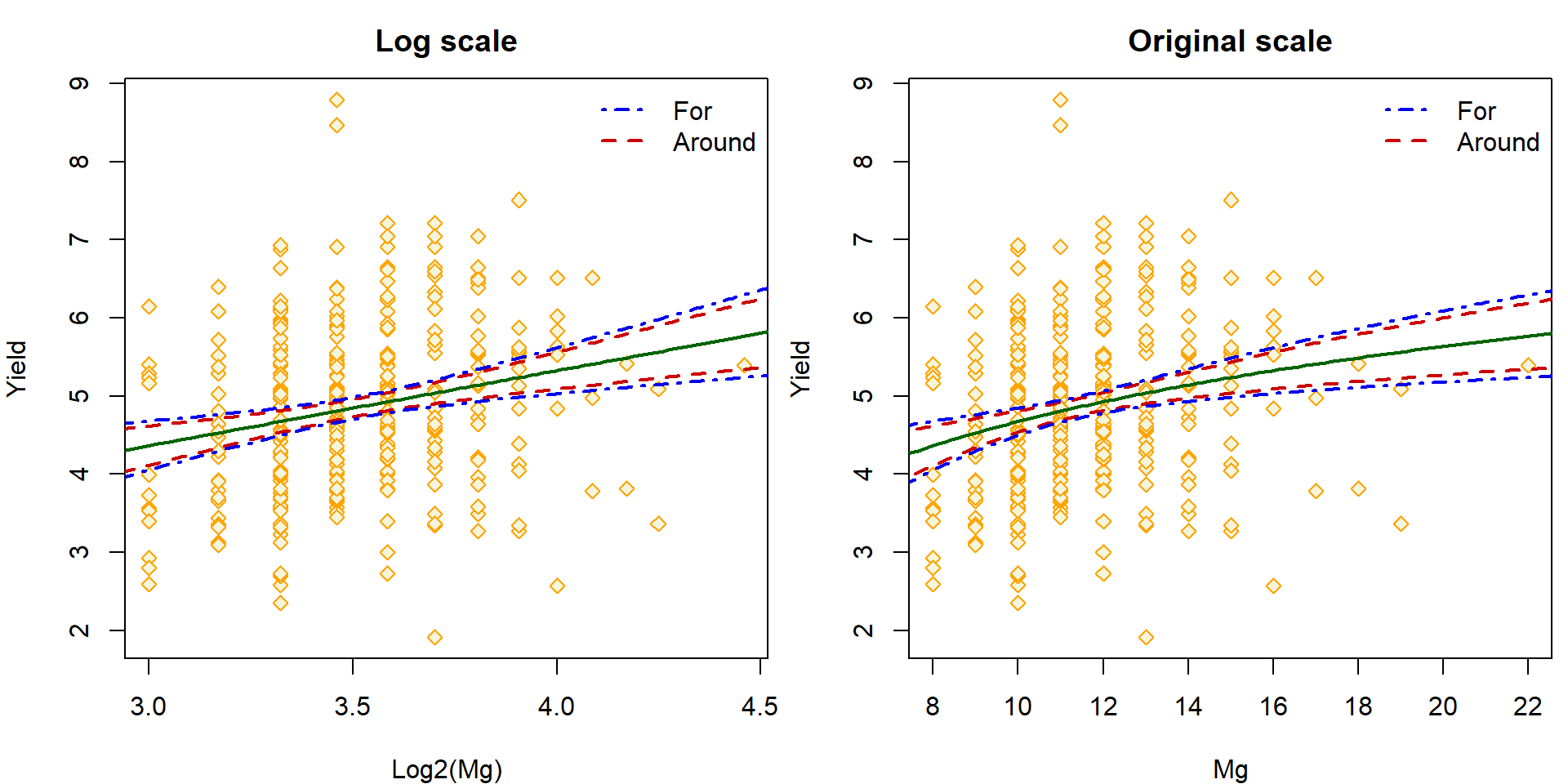
3. Prediction interval (for some new given value of \(\boldsymbol{X}\))
Finally, we will compare both confidence bands constructed above with one more confidence band – the prediction band (which will be again interpreted in a point-wise manner as the first confidence band around the regression line).
The idea is to construct an interval which covers with probability \(1 - \alpha\) the NEW value of the response \(Y\) obtained for \(\boldsymbol{X}\) being set to \(\boldsymbol{x}\).
Compare the following two commands:
predict(aLogMg, newdata = data.frame(Mg = 10), interval = "prediction") ## fit lwr upr
## 1 4.676 2.568 6.784predict(aLogMg, newdata = data.frame(Mg = 10), interval = "confidence") ## fit lwr upr
## 1 4.676 4.537 4.815Manual calculation of the prediction interval can follow the lines below:
s = summary(aLogMg)$sigma
se.fit2 = sqrt(s^2 + (se.fit)^2)
xt_beta + c(-1, 1) * se.fit2 * qt(0.975, df = aLogMg[["df.residual"]])## [1] 2.568 6.784Prediction band - a sequence of prediction intervals for a dense grid of x-values:
pred.aLogMg <- predict(aLogMg, data.frame(Mg = x.Mg), interval = "prediction", level = 0.95)
head(pred.aLogMg)## fit lwr upr
## 1 4.182 2.053 6.311
## 2 4.213 2.086 6.340
## 3 4.244 2.118 6.369
## 4 4.274 2.150 6.397
## 5 4.303 2.181 6.425
## 6 4.332 2.211 6.452Finally, we can visualize the result – using the logarithm scale or the original scale of the magnesium concentration:
par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
## Log scale
plot(yield ~ log2(Mg), data = Dris,
ylab = "Yield", xlab = "log2(Mg)", main = "Log scale",
pch = 23, col = "orange", bg = "beige")
lines(log2(x.Mg), ciEY.aLogMg[, "fit"], lwd = 2, col = "red3")
# Band AROUND the regression line
lines(log2(x.Mg), ciEY.aLogMg[, "lwr"], lwd = 2, col = "red3", lty = 2)
lines(log2(x.Mg), ciEY.aLogMg[, "upr"], lwd = 2, col = "red3", lty = 2)
# Prediction band
lines(log2(x.Mg), pred.aLogMg[, "lwr"], lwd = 2, col = "blue2", lty = 4)
lines(log2(x.Mg), pred.aLogMg[, "upr"], lwd = 2, col = "blue2", lty = 4)
legend("topleft", legend = c("Prediction", "Around the regression line"), bty = "n",
col = c("blue2", "red3"), lty = c(4, 2), lwd = 2)
## Original scale
plot(yield ~ Mg, data = Dris,
ylab = "Yield", xlab = "Mg", main = "Original scale",
pch = 23, col = "orange", bg = "beige")
lines(x.Mg, ciEY.aLogMg[, "fit"], lwd = 2, col = "red3")
# Band AROUND the regression line
lines(x.Mg, ciEY.aLogMg[, "lwr"], lwd = 2, col = "red3", lty = 2)
lines(x.Mg, ciEY.aLogMg[, "upr"], lwd = 2, col = "red3", lty = 2)
# Prediction band
lines(x.Mg, pred.aLogMg[, "lwr"], lwd = 2, col = "blue2", lty = 4)
lines(x.Mg, pred.aLogMg[, "upr"], lwd = 2, col = "blue2", lty = 4)
legend("bottomright", legend = c("Prediction", "Around the regression line"), bty = "n",
col = c("blue2", "red3"), lty = c(4, 2), lwd = 2)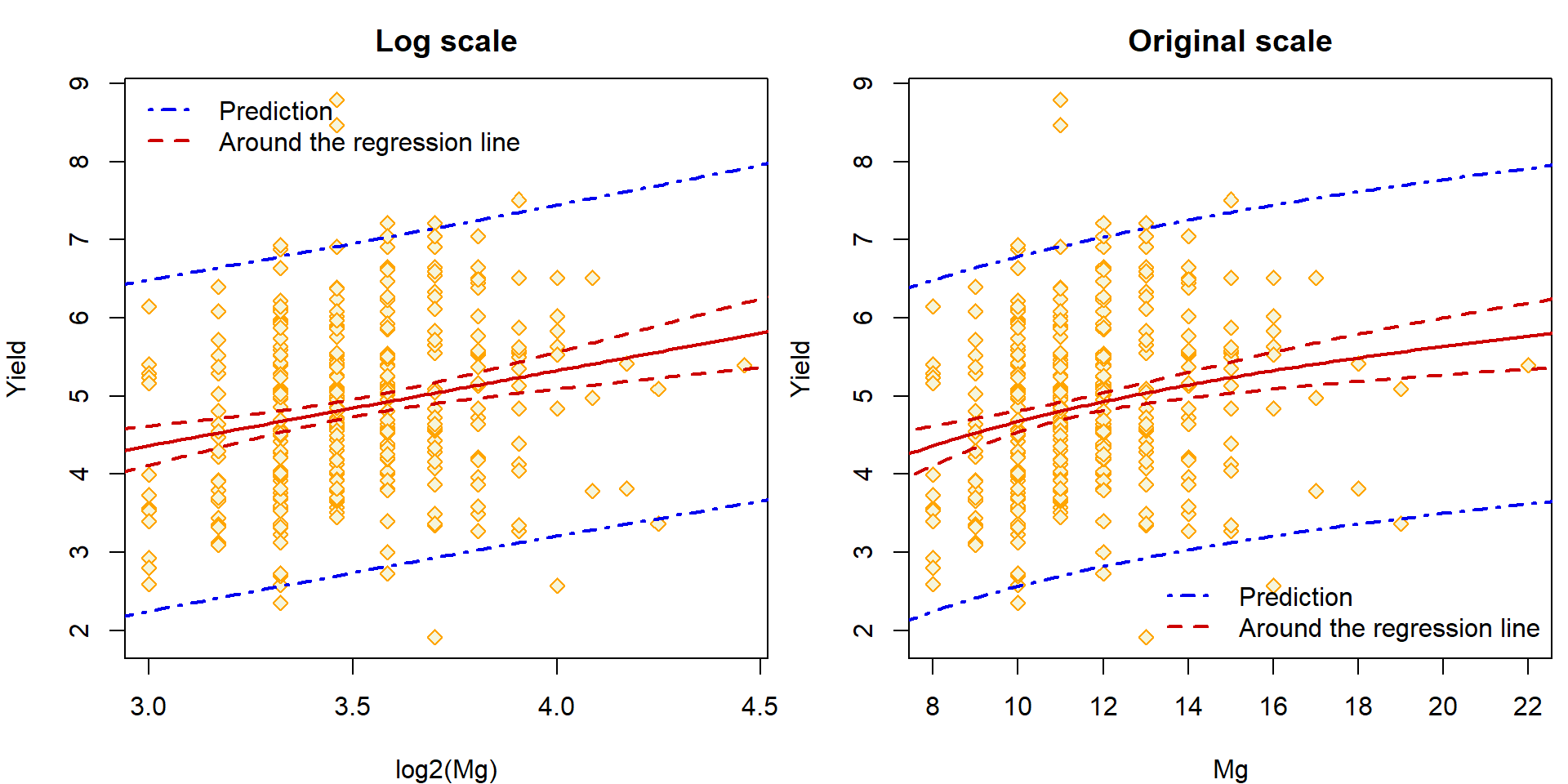
Individual work
- Recall the theoretical foundations of all three confidence bands constructed above. What are the main principal differences?
- What are particular utilization purposes for each of the confidence bands constructed above? What type inferential tool do they offer?