Download this R markdown as: R, Rmd.

Loading the data and libraries

library("mffSM")
library("colorspace")

We want to examine a nitrogen concentration measured at various depths of the peat. Load the data peat below and try to understand the design of the underlying experiment. Focus on various depths in particular.

peat <- read.csv("http://www.karlin.mff.cuni.cz/~vavraj/nmfm334/data/peat.csv", 
                 header = TRUE, stringsAsFactors = TRUE)
dim(peat)
## [1] 148   3
str(peat)
## 'data.frame':    148 obs. of  3 variables:
##  $ group: Factor w/ 4 levels "CB","CB-VJJ",..: 3 3 3 3 3 3 3 3 3 3 ...
##  $ N    : num  0.738 0.847 1.063 1.142 1.272 ...
##  $ depth: int  2 4 6 8 10 12 14 2 4 6 ...
head(peat)
##   group      N depth
## 1   VJJ 0.7384     2
## 2   VJJ 0.8474     4
## 3   VJJ 1.0630     6
## 4   VJJ 1.1419     8
## 5   VJJ 1.2722    10
## 6   VJJ 1.4033    12
summary(peat)
##     group          N             depth      
##  CB    :35   Min.   :0.499   Min.   : 0.00  
##  CB-VJJ:40   1st Qu.:0.899   1st Qu.: 4.00  
##  VJJ   :33   Median :1.034   Median : 8.00  
##  VJJ-CB:40   Mean   :1.077   Mean   : 7.53  
##              3rd Qu.:1.244   3rd Qu.:12.00  
##              Max.   :1.692   Max.   :14.00

Visual exploration

Basic scatterplot for Nitrogen concentration given depth:

XLAB <- "Depth [cm]"
YLAB <- "Nitrogen concentration [weight %]"

XLIM <- range(peat[, "depth"])
YLIM <- range(peat[, "N"])

par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(N ~ depth, data = peat, pch = 21, bg = "lightblue", 
     xlab = XLAB, ylab = YLAB, xlim = XLIM, ylim = YLIM)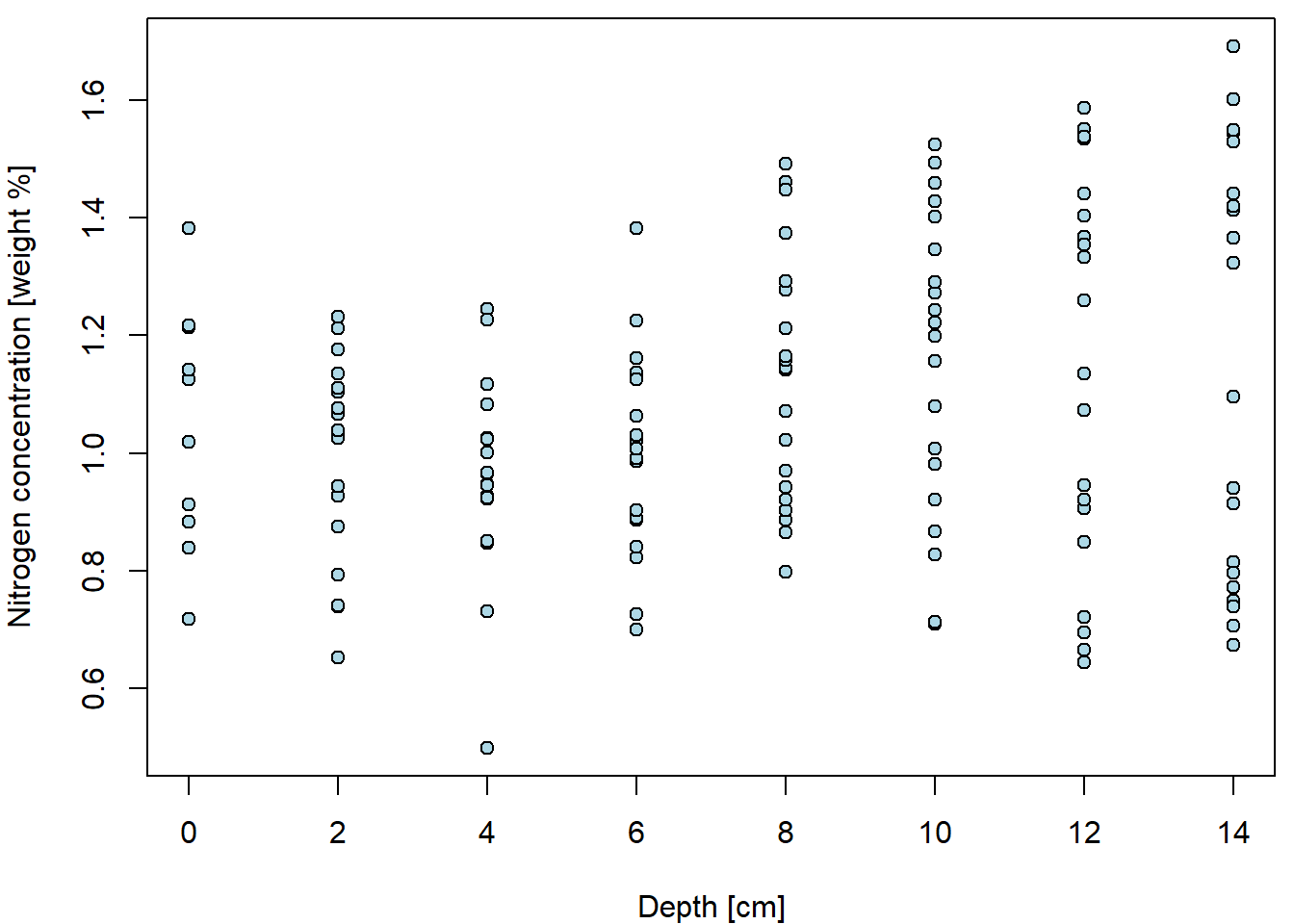

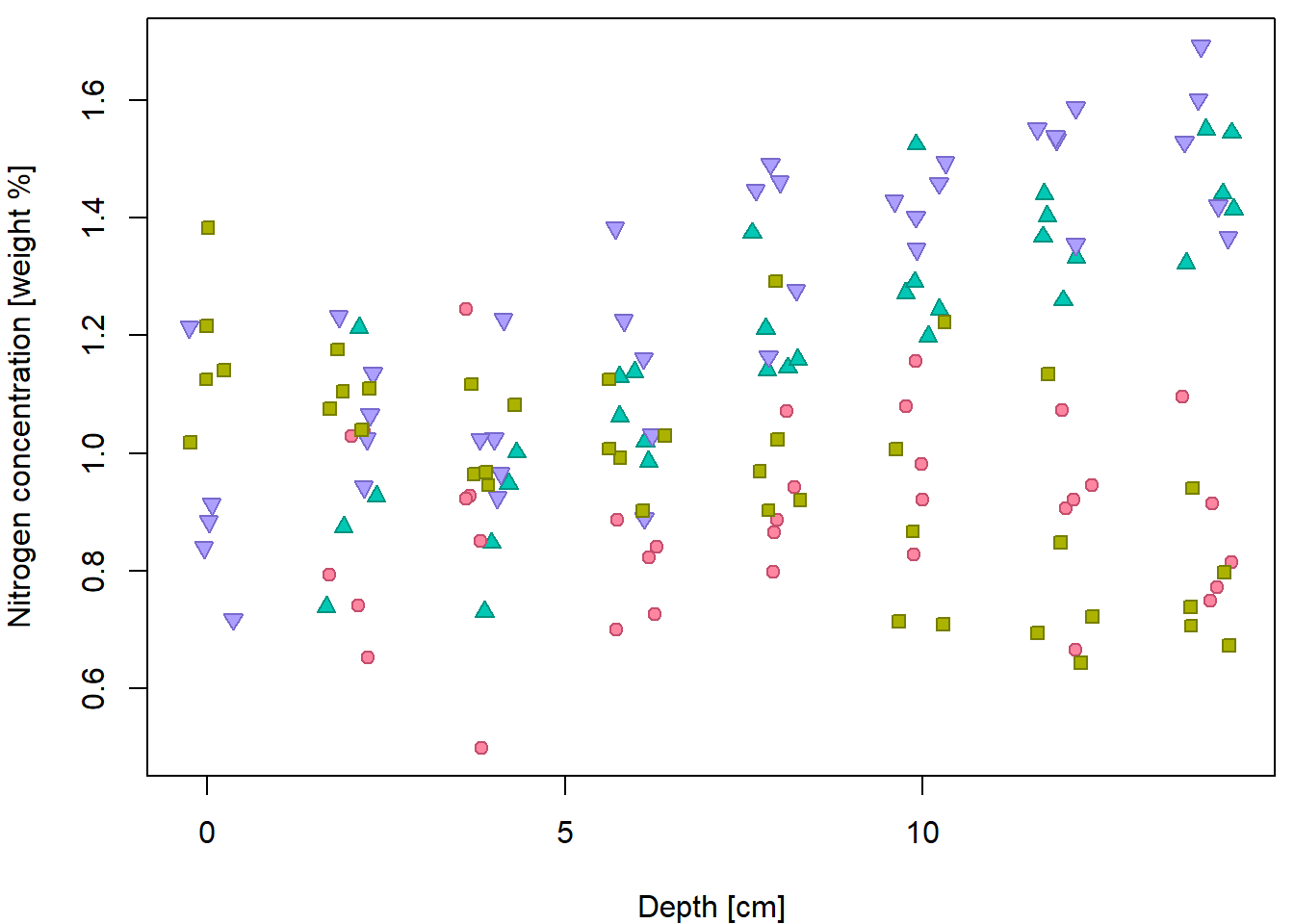
But it can be done better… by distinguishing for different peat types (variable group).

Groups <- levels(peat[, "group"])
print(Groups)
## [1] "CB"     "CB-VJJ" "VJJ"    "VJJ-CB"
PCH <- c(21, 22, 24, 25)
DARK <- rainbow_hcl(4, c = 80, l = 35)
COL <- rainbow_hcl(4, c = 80, l = 50)
BGC <- rainbow_hcl(4, c = 80, l = 70)
names(PCH) <- names(COL) <- names(BGC) <- Groups

par(mfrow = c(2,2), mar = c(4,4,2,1))
for(g in 1:4){
  Group <- Groups[g]
  xx <- subset(peat, group == Group)[, "depth"]
  yy <- subset(peat, group == Group)[, "N"]
  plot(xx, yy, pch = PCH[g], col = COL[g], bg = BGC[g],
       xlab = XLAB, ylab = YLAB, main = Group, xlim = XLIM, ylim = YLIM)
}

Conditional empirical characteristics by groups

tabs <- list()
# g <- 1 # run for one g
for(g in 1:length(Groups)){
  # data subset containing only the g-th group
  subdata <- subset(peat, group == Groups[g])
  # averages for particular depths
  Mean    <- with(subdata, tapply(N, depth, mean))
  # standard deviations for particular depths
  StdDev  <- with(subdata, tapply(N, depth, sd))
  # numbers of observations for particular depths
  ns      <- with(subdata, tapply(N, depth, length))
  
  # cat("\n",Groups[g],"\n")
  # print(Mean)
  # print(StdDev)
  # print(ns)

  tabs[[g]] <- data.frame(Depth = as.numeric(names(Mean)), Mean = Mean, 
                                              Std.Dev = StdDev, n = ns)
  rownames(tabs[[g]]) <- 1:nrow(tabs[[g]])
}  
names(tabs) <- Groups
print(tabs)
## $CB
##   Depth   Mean Std.Dev n
## 1     2 0.8504 0.17437 5
## 2     4 0.8886 0.26575 5
## 3     6 0.7951 0.07906 5
## 4     8 0.9123 0.10257 5
## 5    10 0.9931 0.12951 5
## 6    12 0.9025 0.14771 5
## 7    14 0.8694 0.14203 5
## 
## $`CB-VJJ`
##   Depth   Mean Std.Dev n
## 1     0 1.1769 0.13512 5
## 2     2 1.1012 0.05042 5
## 3     4 1.0153 0.07849 5
## 4     6 1.0114 0.08000 5
## 5     8 1.0216 0.15842 5
## 6    10 0.9036 0.21678 5
## 7    12 0.8086 0.19743 5
## 8    14 0.7710 0.10511 5
## 
## $VJJ
##   Depth   Mean Std.Dev n
## 1     2 0.9381 0.19973 4
## 2     4 0.8817 0.11941 4
## 3     6 1.0673 0.06671 5
## 4     8 1.2065 0.09810 5
## 5    10 1.3062 0.12734 5
## 6    12 1.3611 0.06927 5
## 7    14 1.4550 0.09526 5
## 
## $`VJJ-CB`
##   Depth   Mean Std.Dev n
## 1     0 0.9132 0.18372 5
## 2     2 1.0804 0.10998 5
## 3     4 1.0331 0.11638 5
## 4     6 1.1380 0.18807 5
## 5     8 1.3686 0.14144 5
## 6    10 1.4260 0.05604 5
## 7    12 1.5132 0.09093 5
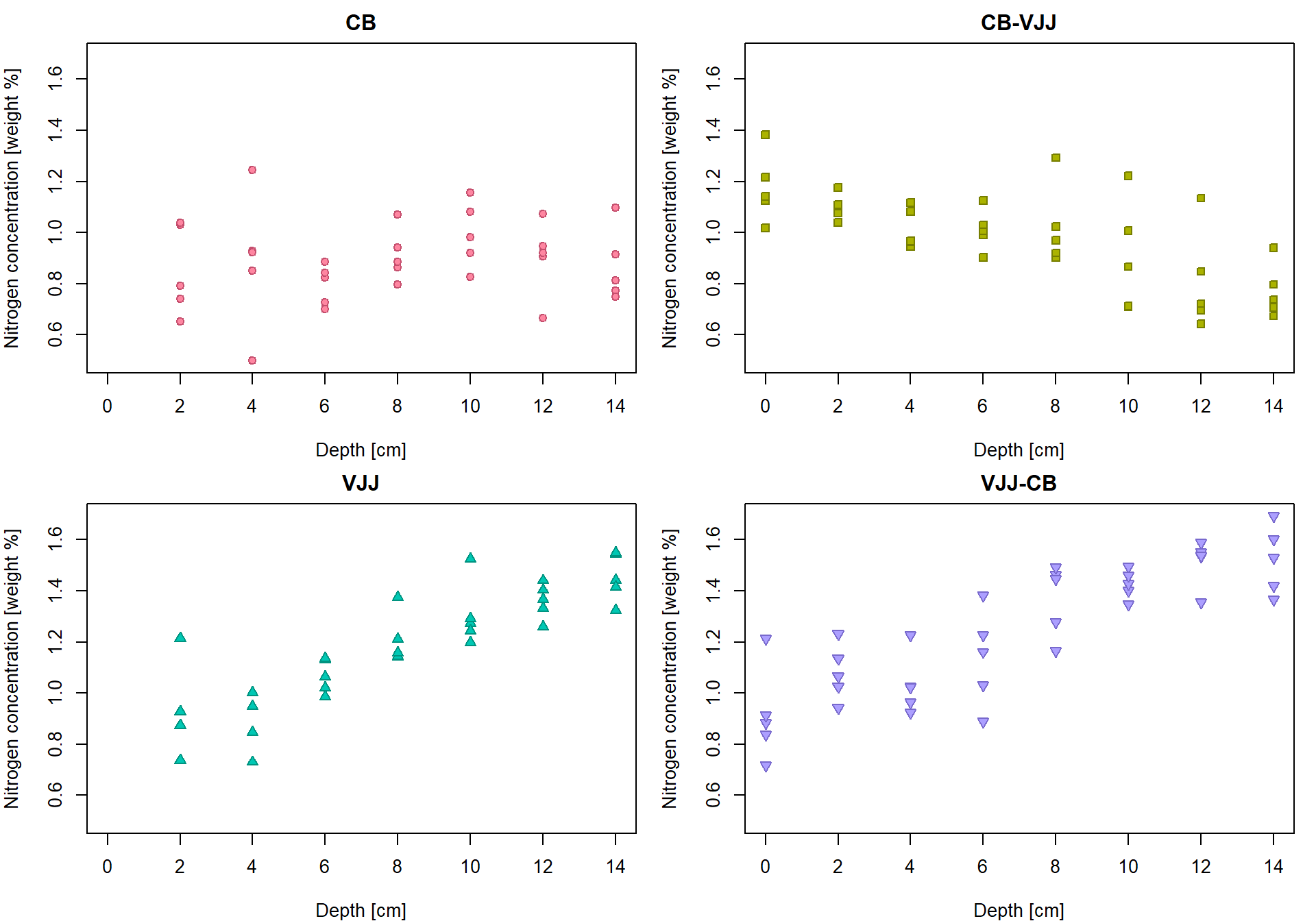
## 8    14 1.5221 0.13198 5

Insert the group averages into the original plot

par(mfrow = c(2,2), mar = c(4,4,2,1))
for (g in 1:4){
  Group <- Groups[g]
  xx <- subset(peat, group == Group)[, "depth"]
  yy <- subset(peat, group == Group)[, "N"]
  plot(xx, yy, pch = PCH[g], col = COL[g], bg = BGC[g], 
               xlab = XLAB, ylab = YLAB, main = Group, xlim = XLIM, ylim = YLIM)
  lines(tabs[[g]][, "Depth"], tabs[[g]][, "Mean"], type = "b",
        pch = 23, lty = 2, cex = 2, col = COL[g], bg = BGC[g])
}

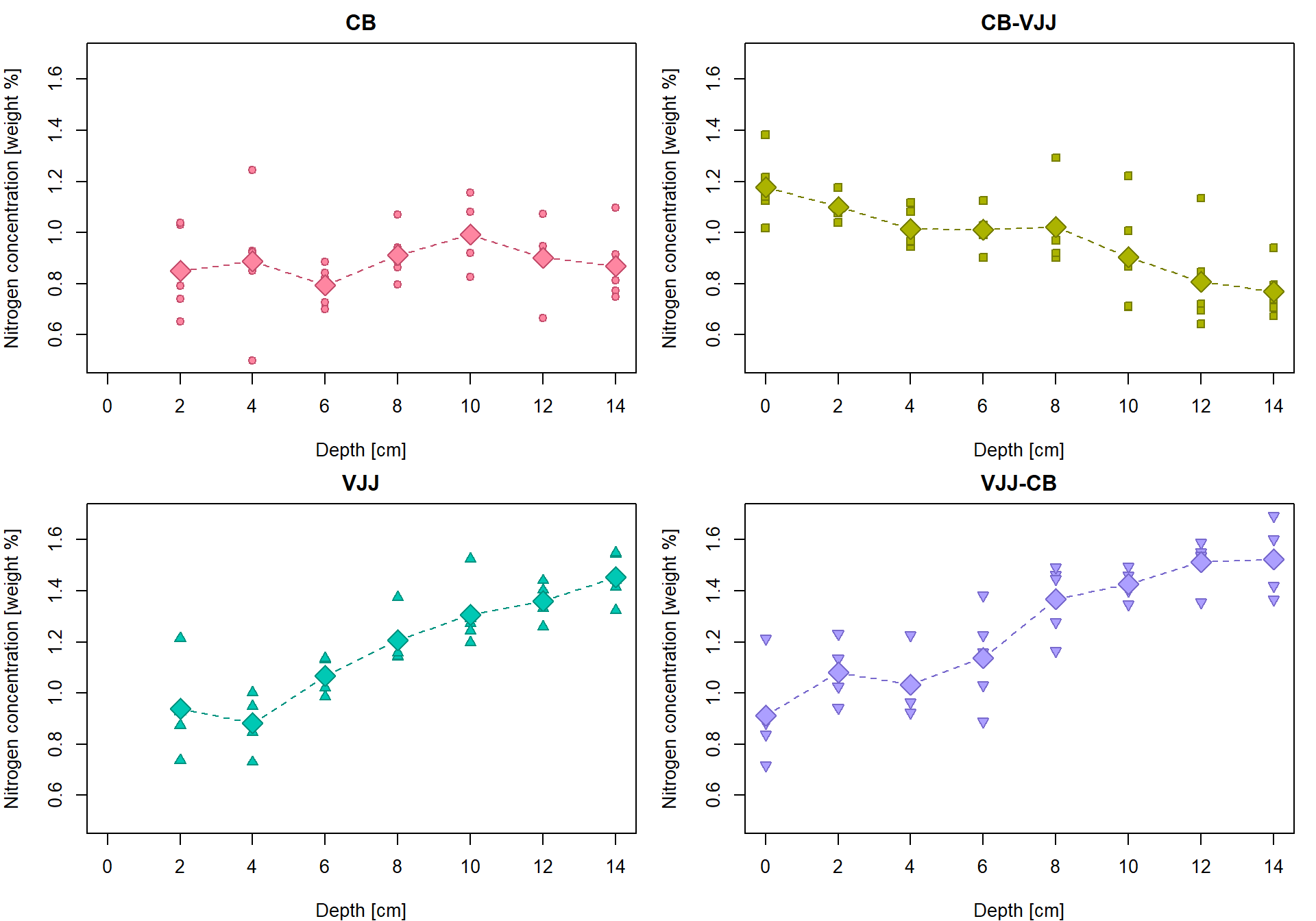
Linear regression line for the group “CB-VJJ”

Let’s fit the least-squares estimated of the regression line parameters with lm:

Group <- "CB-VJJ"  
g <- 2 

fit1 <- lm(N ~ depth, data = peat, subset = (group == Group))
print(fit1)
## 
## Call:
## lm(formula = N ~ depth, data = peat, subset = (group == Group))
## 
## Coefficients:
## (Intercept)        depth  
##      1.1691      -0.0276

The regression line establishes a simple relationship between the nitrogen concentration (Y values) and the depth of the measurement (X values).

Yvalues <- peat$N[peat$group == Group]
Xvalues <- peat$depth[peat$group == Group]

Y <- function(a, b, x){
# a simple line parametrization with the intercept 'a' and the slope `b`
  return(a + b * x) 
}

par(mfrow = c(1,1), mar = c(4,4,2,1))
# the underlying data
plot(Yvalues ~ Xvalues, pch = PCH[Group], col = COL[Group], bg = BGC[Group], 
     xlab = XLAB, ylab = YLAB, main = Group, xlim = XLIM, ylim = YLIM) 
# empirical group means
lines(tabs[[g]][, "Depth"], tabs[[g]][, "Mean"], type = "b",
      pch = 23, lty = 2, cex = 2, col = COL[g], bg = BGC[g])
# regression line given by the LS estimates (for the specific values of the depth)
points(Y(fit1$coeff[1], fit1$coeff[2], Xvalues) ~ Xvalues, 
       pch = 16, col = DARK[g], bg = BGC[g],  cex = 1.5)
# regression line by the 'lm()' function (for the whole real line)
abline(fit1, col = DARK[g], lwd = 2)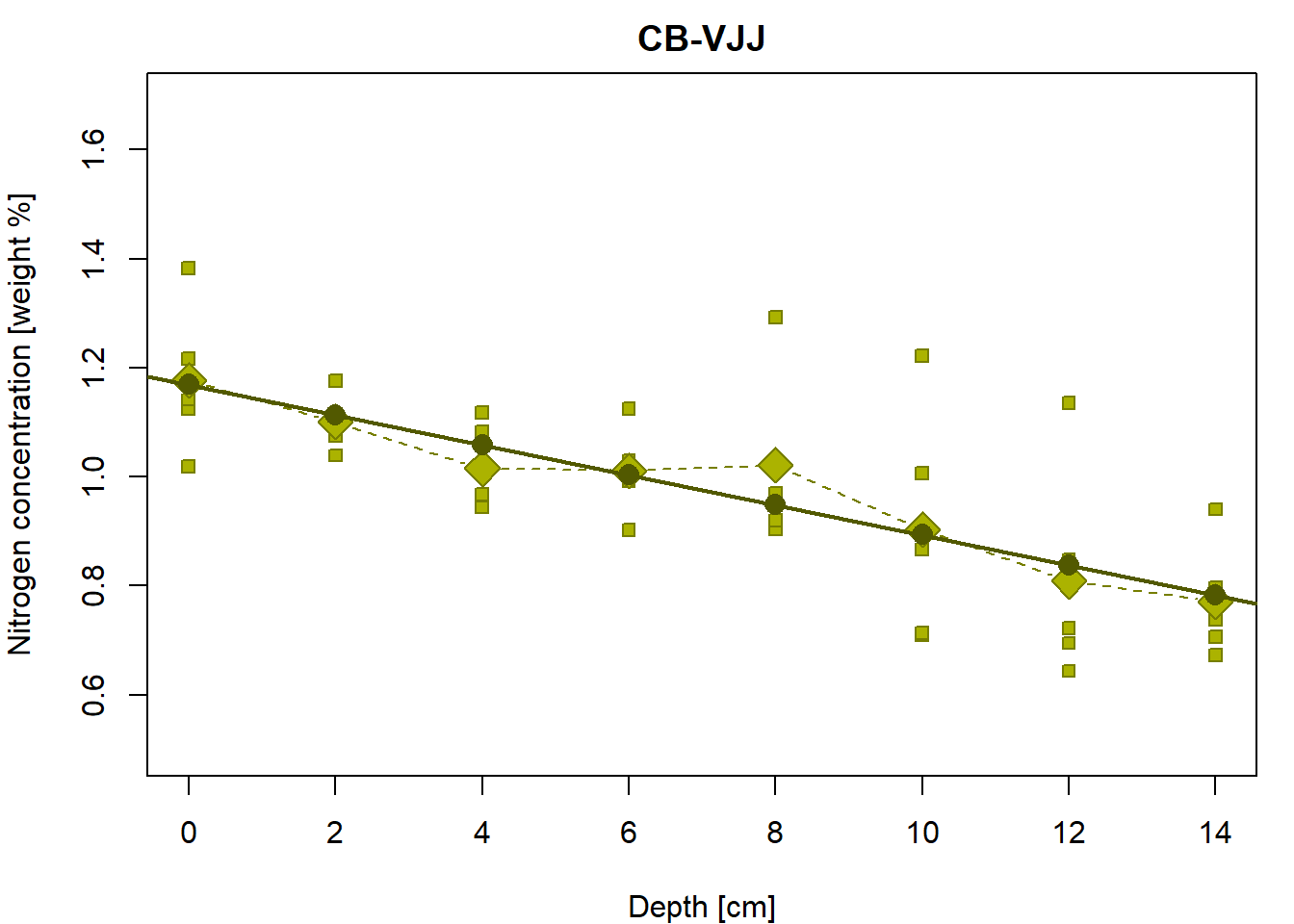

Object fit1 contains many interesting quantities… fit1 is in fact a list and its components are accessible either as fit1[["COMPONENT"]] or as fit1$COMPONENT

names(fit1)
##  [1] "coefficients"  "residuals"     "effects"       "rank"          "fitted.values" "assign"       
##  [7] "qr"            "df.residual"   "xlevels"       "call"          "terms"         "model"

Estimated coefficients (intercept and slope):

fit1[["coefficients"]]
## (Intercept)       depth 
##     1.16907    -0.02755
fit1$coefficients
## (Intercept)       depth 
##     1.16907    -0.02755
coef(fit1)                   # hat{beta}
## (Intercept)       depth 
##     1.16907    -0.02755

Fitted values:

fit1[["fitted.values"]]
##    109    110    111    112    113    114    115    116    117    118    119    120    121    122    123 
## 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 
##    124    125    126    127    128    129    130    131    132    133    134    135    136    137    138 
## 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 
##    139    140    141    142    143    144    145    146    147    148 
## 0.8384 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 0.7833
fitted(fit1)                 # hat{Y}
##    109    110    111    112    113    114    115    116    117    118    119    120    121    122    123 
## 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 
##    124    125    126    127    128    129    130    131    132    133    134    135    136    137    138 
## 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 
##    139    140    141    142    143    144    145    146    147    148 
## 0.8384 0.7833 1.1691 1.1140 1.0589 1.0038 0.9487 0.8935 0.8384 0.7833
Yhat = cbind(1,Xvalues) %*% coef(fit1)
all.equal(as.numeric(Yhat), unname(fitted(fit1)))  
## [1] TRUE

Residuals:

fit1[["residuals"]]
##       109       110       111       112       113       114       115       116       117       118       119 
## -0.043626 -0.009146 -0.113661 -0.101298 -0.045701 -0.184711 -0.194907 -0.110234 -0.150839 -0.003993  0.023492 
##       120       121       122       123       124       125       126       127       128       129       130 
## -0.012196  0.074187  0.113269  0.009912  0.013481  0.047742 -0.074664 -0.094068  0.121601  0.343741  0.329025 
##       131       132       133       134       135       136       137       138       139       140       141 
##  0.296565  0.157088  0.213630  0.062043 -0.091651  0.003871  0.020786 -0.026919 -0.143776 -0.076928 -0.027662 
##       142       143       144       145       146       147       148 
## -0.038311  0.058281  0.026092 -0.028355 -0.180401 -0.116814 -0.044944
residuals(fit1)              # U = Y - hat{Y}
##       109       110       111       112       113       114       115       116       117       118       119 
## -0.043626 -0.009146 -0.113661 -0.101298 -0.045701 -0.184711 -0.194907 -0.110234 -0.150839 -0.003993  0.023492 
##       120       121       122       123       124       125       126       127       128       129       130 
## -0.012196  0.074187  0.113269  0.009912  0.013481  0.047742 -0.074664 -0.094068  0.121601  0.343741  0.329025 
##       131       132       133       134       135       136       137       138       139       140       141 
##  0.296565  0.157088  0.213630  0.062043 -0.091651  0.003871  0.020786 -0.026919 -0.143776 -0.076928 -0.027662 
##       142       143       144       145       146       147       148 
## -0.038311  0.058281  0.026092 -0.028355 -0.180401 -0.116814 -0.044944
(Res = c(Yvalues - Yhat))
##  [1] -0.043626 -0.009146 -0.113661 -0.101298 -0.045701 -0.184711 -0.194907 -0.110234 -0.150839 -0.003993
## [11]  0.023492 -0.012196  0.074187  0.113269  0.009912  0.013481  0.047742 -0.074664 -0.094068  0.121601
## [21]  0.343741  0.329025  0.296565  0.157088  0.213630  0.062043 -0.091651  0.003871  0.020786 -0.026919
## [31] -0.143776 -0.076928 -0.027662 -0.038311  0.058281  0.026092 -0.028355 -0.180401 -0.116814 -0.044944
all.equal(as.numeric(Res),unname(residuals(fit1))) 
## [1] TRUE

Rank and degrees of freedom:

fit1[["rank"]]               # r
## [1] 2
fit1[["df.residual"]]        # n - r
## [1] 38
(r = qr(cbind(1,Xvalues))$rank)
## [1] 2
n = length(Yvalues)
n - r
## [1] 38

Basic inferential quantities can be extracted from the object returned by summary of lm fit:

summary(fit1)      
## 
## Call:
## lm(formula = N ~ depth, data = peat, subset = (group == Group))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.1949 -0.0923 -0.0196  0.0504  0.3437 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.16907    0.03819   30.61  < 2e-16 ***
## depth       -0.02755    0.00456   -6.04  5.1e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.132 on 38 degrees of freedom
## Multiple R-squared:  0.489,  Adjusted R-squared:  0.476 
## F-statistic: 36.4 on 1 and 38 DF,  p-value: 5.08e-07

First summary is simple summary of the residuals:

summary(Res)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -0.1949 -0.0923 -0.0196  0.0000  0.0504  0.3437

Residual sum of squares and residual standard error

(SSe <- deviance(fit1))        # SS_e
## [1] 0.6651
sum((fit1$residuals)^2)        # the same
## [1] 0.6651
sqrt(SSe / (n-r))              # residual standard error
## [1] 0.1323

Matrix \(\mathsf{MS}_e \cdot (\mathbb{X}^\top \mathbb{X})^{-1}\)

vcov(fit1)
##             (Intercept)      depth
## (Intercept)   0.0014586 -1.459e-04
## depth        -0.0001459  2.084e-05

Standard error terms (square root of the diagonal)

sqrt(diag(vcov(fit1)))
## (Intercept)       depth 
##    0.038191    0.004565

Correlation matrix derived from vcov(fit1)

cov2cor(vcov(fit1))
##             (Intercept)   depth
## (Intercept)      1.0000 -0.8367
## depth           -0.8367  1.0000

Confidence intervals for regression coefficients

confint(fit1, level= 0.95)
##                2.5 %   97.5 %
## (Intercept)  1.09176  1.24638
## depth       -0.03679 -0.01831

Intercept only model for the group “CB-VJJ”

What is it all good for? Another regression line is used to fit the same data. What is the main difference between fit1 and fit0?

fit0 <- lm(N ~ 1, data = peat, subset = (group == Group))
summary(fit0)
## 
## Call:
## lm(formula = N ~ 1, data = peat, subset = (group == Group))
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -0.333 -0.114  0.023  0.136  0.406 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.9762     0.0289    33.8   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.183 on 39 degrees of freedom

The model fits the regression line which is always parallel with the x-axis (thus, the slope is always zero)

Y <- function(a, x){
# a simple line parametrization with the intercept 'a' and zero slope
  return(a + 0 * x) 
}

# the same Y values for each X value... why? 
Y(fit0$coeff[1], Xvalues)
##  [1] 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762
## [16] 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762
## [31] 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762 0.9762
par(mfrow = c(1,1), mar = c(4,4,2,1))
# the underlying data
plot(Yvalues~Xvalues, pch = PCH[Group], col = COL[Group], bg = BGC[Group],
     xlab = XLAB, ylab = YLAB, main = Group, xlim = XLIM, ylim = YLIM) 
# empirical group means
lines(tabs[[g]][, "Depth"], tabs[[g]][, "Mean"], type = "b",
      pch = 23, lty = 2, cex = 2, col = COL[g], bg = BGC[g])
# regression line given by the LS estimates (for the specific values of depth)
points(Y(fit0$coeff[1], Xvalues)~Xvalues, 
       pch = 16, col = DARK[g], bg = BGC[2], cex = 1.5)
# regression line by the 'lm()' function (for the whole real line)
abline(fit0, col = DARK[g], lwd = 2)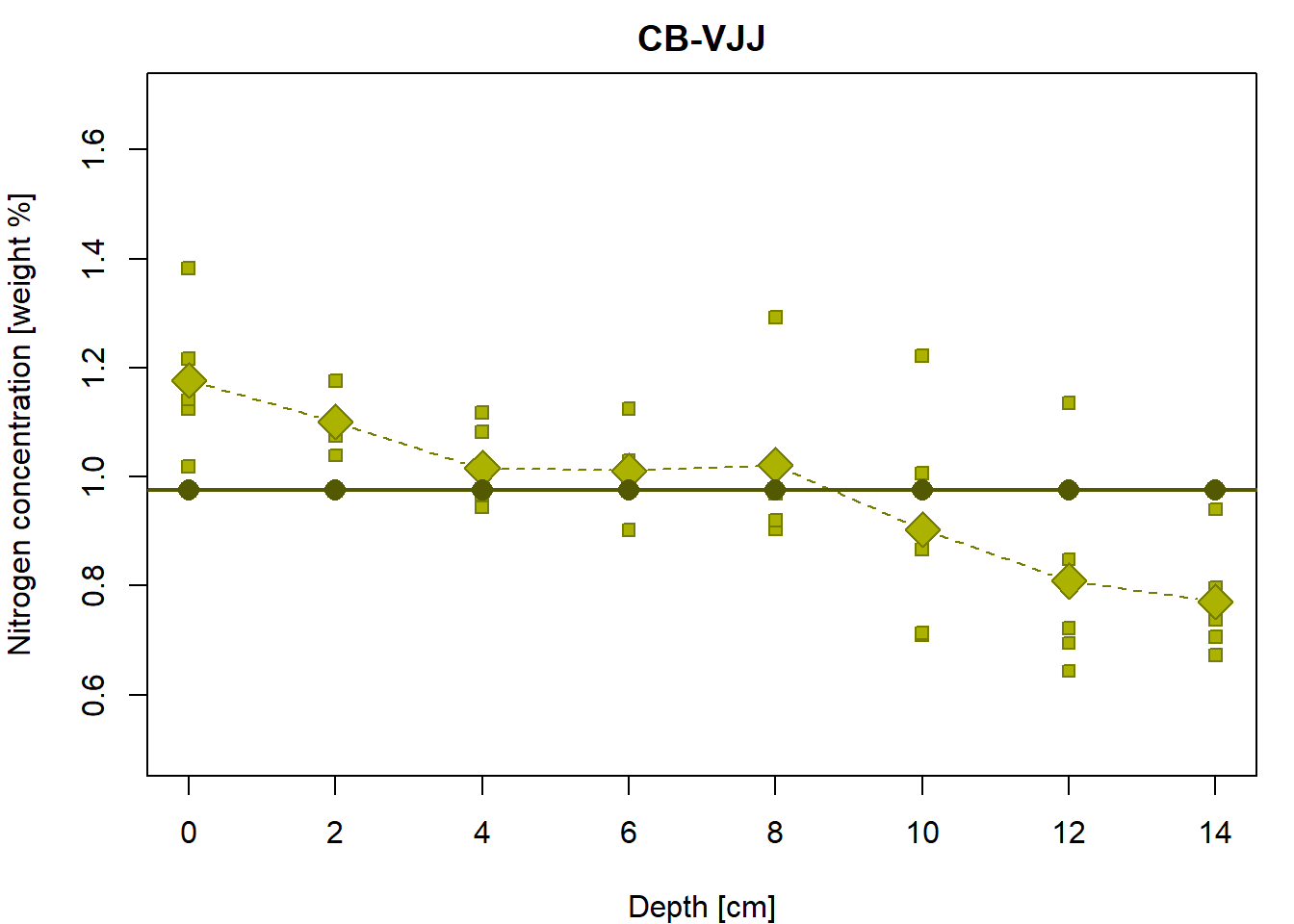

Do you see any relationship with the following?

mean(Yvalues)           # beta coefficient
## [1] 0.9762
sd(Yvalues)             # residual standard error
## [1] 0.1828
sd(Yvalues)/sqrt(n)     # estimated sd of beta
## [1] 0.0289

Total sum of squares:

deviance(fit0)          # SS_T (= SS_e of fit0)
## [1] 1.303
sum((Yvalues - mean(Yvalues))^2)
## [1] 1.303

Overall F-test (once more):

summary(fit1)
## 
## Call:
## lm(formula = N ~ depth, data = peat, subset = (group == Group))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.1949 -0.0923 -0.0196  0.0504  0.3437 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.16907    0.03819   30.61  < 2e-16 ***
## depth       -0.02755    0.00456   -6.04  5.1e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.132 on 38 degrees of freedom
## Multiple R-squared:  0.489,  Adjusted R-squared:  0.476 
## F-statistic: 36.4 on 1 and 38 DF,  p-value: 5.08e-07
anova(fit0, fit1)
## Analysis of Variance Table
## 
## Model 1: N ~ 1
## Model 2: N ~ depth
##   Res.Df   RSS Df Sum of Sq    F  Pr(>F)    
## 1     39 1.303                              
## 2     38 0.665  1     0.638 36.4 5.1e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Compare to standard correlation test:

cor.test(Xvalues, Yvalues)
## 
##  Pearson's product-moment correlation
## 
## data:  Xvalues and Yvalues
## t = -6, df = 38, p-value = 5e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.8302 -0.4963
## sample estimates:
##     cor 
## -0.6996

Depth-as-factor model for the group “CB-VJJ”

Compare fit0 and fit1 with the model where each depth level is considered separately:

(fit2 = lm(N ~ -1 + as.factor(depth), data = peat, subset = (group == Group)))
## 
## Call:
## lm(formula = N ~ -1 + as.factor(depth), data = peat, subset = (group == 
##     Group))
## 
## Coefficients:
##  as.factor(depth)0   as.factor(depth)2   as.factor(depth)4   as.factor(depth)6   as.factor(depth)8  
##              1.177               1.101               1.015               1.011               1.022  
## as.factor(depth)10  as.factor(depth)12  as.factor(depth)14  
##              0.904               0.809               0.771
par(mfrow = c(1,1), mar = c(4,4,2,1))
# the underlying data
plot(Yvalues~Xvalues,pch = PCH[Group], col = COL[Group], bg = BGC[Group], 
               xlab = XLAB, ylab = YLAB, main = Group, xlim = XLIM, ylim = YLIM) 
# empirical group means
lines(tabs[[g]][, "Depth"], tabs[[g]][, "Mean"], type="b",
      pch = 23, cex = 2, col = COL[g], bg = BGC[g])
# regression line given by the LS estimates (for the specific values of depth)
points(subset(peat, group==Group)$depth, fitted(fit2), pch=20, cex=2, col=DARK[g])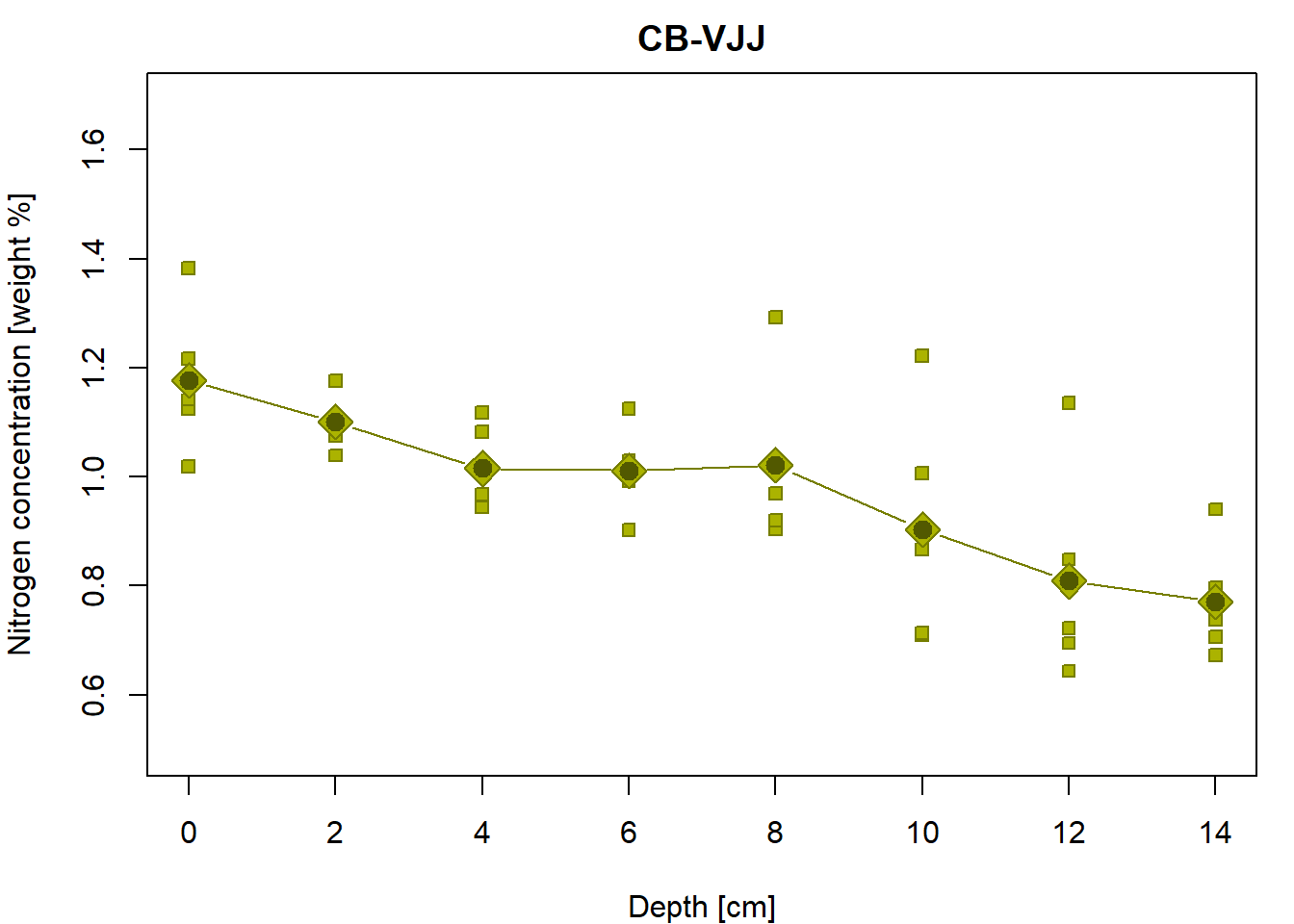

Is it possible to judge (just visually) from the third column whether one assumption of the classical linear model is satisfied? Which assumption?

print(tabs[[Group]])
##   Depth   Mean Std.Dev n
## 1     0 1.1769 0.13512 5
## 2     2 1.1012 0.05042 5
## 3     4 1.0153 0.07849 5
## 4     6 1.0114 0.08000 5
## 5     8 1.0216 0.15842 5
## 6    10 0.9036 0.21678 5
## 7    12 0.8086 0.19743 5
## 8    14 0.7710 0.10511 5

Numeric computations behind lm

We fit the simple linear regression line estimate once again with additional argument:

fit1 <- lm(N ~ depth, data = peat, subset = (group == Group), x = TRUE)
names(fit1)
##  [1] "coefficients"  "residuals"     "effects"       "rank"          "fitted.values" "assign"       
##  [7] "qr"            "df.residual"   "xlevels"       "call"          "terms"         "model"        
## [13] "x"

The fit1 object additionally contains an element x, the model matrix \(\mathbb{X}\):

X <- fit1[["x"]]
# X <- model.matrix(N ~ depth, peat, subset = (group == Group)) # or directly
print(X)
##     (Intercept) depth
## 109           1     0
## 110           1     2
## 111           1     4
## 112           1     6
## 113           1     8
## 114           1    10
## 115           1    12
## 116           1    14
## 117           1     0
## 118           1     2
## 119           1     4
## 120           1     6
## 121           1     8
## 122           1    10
## 123           1    12
## 124           1    14
## 125           1     0
## 126           1     2
## 127           1     4
## 128           1     6
## 129           1     8
## 130           1    10
## 131           1    12
## 132           1    14
## 133           1     0
## 134           1     2
## 135           1     4
## 136           1     6
## 137           1     8
## 138           1    10
## 139           1    12
## 140           1    14
## 141           1     0
## 142           1     2
## 143           1     4
## 144           1     6
## 145           1     8
## 146           1    10
## 147           1    12
## 148           1    14
## attr(,"assign")
## [1] 0 1

Response \(\mathbf{Y}\) could be obtained with y = TRUE or taken from the data:

y <- subset(peat, group == Group)[, "N"]
print(y)
##  [1] 1.1254 1.1048 0.9452 0.9025 0.9030 0.7088 0.6435 0.6731 1.0182 1.1100 1.0824 0.9916 1.0228 1.0068 0.8484
## [16] 0.7968 1.2168 1.0393 0.9648 1.1254 1.2924 1.2226 1.1350 0.9404 1.3827 1.1760 0.9672 1.0076 0.9694 0.8666
## [31] 0.6947 0.7064 1.1414 1.0757 1.1171 1.0298 0.9203 0.7131 0.7216 0.7384

Model fitting \(\widehat{\mathbf{\beta}} = \left(\mathbb{X}^\top \mathbb{X}\right)^{-1} \mathbb{X}^\top \mathbf{Y}\):

(XtX <- t(X) %*% X)              # What are the elements of XtX?
##             (Intercept) depth
## (Intercept)          40   280
## depth               280  2800
(Xty <- t(X) %*% y)              # What are the elements of Xty?
##               [,1]
## (Intercept)  39.05
## depth       250.19
(b <- solve(XtX, Xty))           # beta
##                 [,1]
## (Intercept)  1.16907
## depth       -0.02755
coef(fit1)
## (Intercept)       depth 
##     1.16907    -0.02755

Projection matrix \(\mathbb{H} = \mathbb{X} \left(\mathbb{X}^\top \mathbb{X}\right)^{-1} \mathbb{X}^\top\):

H <- X %*% solve(XtX) %*% t(X)    # What is its purpose?
dim(H)
## [1] 40 40
all.equal(c(H%*%y),unname(fitted(fit1)))  
## [1] TRUE

Numerically efficient way how to get it (using the QR decomposition):

Q <- qr.Q(fit1[["qr"]])  # Q matrix (orthogonal columns)
H <- qr.Q(fit1[["qr"]]) %*% t(qr.Q(fit1[["qr"]]))
dim(H)
## [1] 40 40
H[1:10, 1:10]     # part of H matrix
##             [,1]      [,2]       [,3]    [,4]    [,5]       [,6]      [,7]       [,8]     [,9]     [,10]
##  [1,]  8.333e-02  0.066667  5.000e-02 0.03333 0.01667 -6.939e-18 -0.016667 -3.333e-02  0.08333  0.066667
##  [2,]  6.667e-02  0.054762  4.286e-02 0.03095 0.01905  7.143e-03 -0.004762 -1.667e-02  0.06667  0.054762
##  [3,]  5.000e-02  0.042857  3.571e-02 0.02857 0.02143  1.429e-02  0.007143 -3.469e-18  0.05000  0.042857
##  [4,]  3.333e-02  0.030952  2.857e-02 0.02619 0.02381  2.143e-02  0.019048  1.667e-02  0.03333  0.030952
##  [5,]  1.667e-02  0.019048  2.143e-02 0.02381 0.02619  2.857e-02  0.030952  3.333e-02  0.01667  0.019048
##  [6,] -6.939e-18  0.007143  1.429e-02 0.02143 0.02857  3.571e-02  0.042857  5.000e-02  0.00000  0.007143
##  [7,] -1.667e-02 -0.004762  7.143e-03 0.01905 0.03095  4.286e-02  0.054762  6.667e-02 -0.01667 -0.004762
##  [8,] -3.333e-02 -0.016667 -3.469e-18 0.01667 0.03333  5.000e-02  0.066667  8.333e-02 -0.03333 -0.016667
##  [9,]  8.333e-02  0.066667  5.000e-02 0.03333 0.01667  0.000e+00 -0.016667 -3.333e-02  0.08333  0.066667
## [10,]  6.667e-02  0.054762  4.286e-02 0.03095 0.01905  7.143e-03 -0.004762 -1.667e-02  0.06667  0.054762
max(c(abs(X %*% solve(XtX) %*% t(X) - H))) # numerically zero
## [1] 6.939e-17

Fitted values \(\widehat{\mathbf{Y}}\):

yhat  <- H %*% y
yhat2 <- X %*% b
summary(yhat - yhat2)             # Numerically only zeros
##        V1           
##  Min.   :-6.66e-16  
##  1st Qu.:-2.78e-16  
##  Median : 1.11e-16  
##  Mean   : 1.11e-17  
##  3rd Qu.: 2.50e-16  
##  Max.   : 5.55e-16

Residuals \(\mathbf{U}\):

mean(y - yhat)                    # Numerically zero 
## [1] -7.217e-17

Complement of the projection matrix \(\mathbb{M}\) - projection matrix into the space of residuals

M <- diag(nrow(H)) - H
all.equal(c(M%*%y), unname(fit1$residuals))
## [1] TRUE

Residuals are orthogonal to the columns of \(\mathbb{X}\), i.e. \(\mathbb{M} \cdot \mathbb{X} = \mathbb{O}\) (zero matrix):

max(abs(c(M%*%X)))
## [1] 5.329e-15

Therefore, since \(\mathbf{U} = \mathbb{M} \cdot \mathbf{Y}\), \[\mathbb{X}^\top \cdot \mathbf{U} = \mathbb{X}^\top \cdot \mathbb{M} \cdot \mathbf{Y} = (\mathbb{M} \cdot \mathbb{X})^\top \cdot \mathbf{Y} = \mathbf{0}.\] Because the vector of all ones \(\mathbf{1}\) is a column of \(\mathbb{X}\), also \(\mathbf{1}^\top \cdot \mathbf{U} = 0\). We obtain that the sum of residuals in a linear model with intercept must equal 0. More generally, residuals are orthogonal to the columns of \(\mathbb{X}\).

\(\mathsf{SS}_e\) (residual sum of squares):

deviance(fit1)
## [1] 0.6651
(SSe  <- as.numeric(t(y) %*% M %*% y))
## [1] 0.6651
(SSe2 <- as.numeric(crossprod(y - yhat)))  # The same
## [1] 0.6651

Residual mean square \(\mathsf{MS_e}\) (and its square root):

(df <- length(y) - r)
## [1] 38
(s2 <- SSe / df)
## [1] 0.0175
(s <- sqrt(s2))
## [1] 0.1323
summary(fit1)
## 
## Call:
## lm(formula = N ~ depth, data = peat, subset = (group == Group), 
##     x = TRUE)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.1949 -0.0923 -0.0196  0.0504  0.3437 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.16907    0.03819   30.61  < 2e-16 ***
## depth       -0.02755    0.00456   -6.04  5.1e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.132 on 38 degrees of freedom
## Multiple R-squared:  0.489,  Adjusted R-squared:  0.476 
## F-statistic: 36.4 on 1 and 38 DF,  p-value: 5.08e-07

What are we going to calculate by this? What is its purpose? Can it be found somewhere in summary(fit1)?

deviance(fit0)
## [1] 1.303
(SST <- as.numeric(crossprod(y - mean(y))))
## [1] 1.303
(WhatIsIt <- 1 - SSe / SST)
## [1] 0.4895

Coefficient of determination - square of the coefficient of (multiple). Also, a square of correlation between response Y and regressor X.

cor(Xvalues,Yvalues)^2     
## [1] 0.4895

Variance and standard deviations of the regression coefficients’ estimates. Why is it important or useful? Can you find them somewhere in summary(fit1)?

(varb <- s2 * solve(XtX))
##             (Intercept)      depth
## (Intercept)   0.0014586 -1.459e-04
## depth        -0.0001459  2.084e-05
(sb1 <- sqrt(varb[1, 1]))
## [1] 0.03819
(sb2 <- sqrt(varb[2, 2]))
## [1] 0.004565
summary(fit1)
## 
## Call:
## lm(formula = N ~ depth, data = peat, subset = (group == Group), 
##     x = TRUE)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.1949 -0.0923 -0.0196  0.0504  0.3437 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.16907    0.03819   30.61  < 2e-16 ***
## depth       -0.02755    0.00456   -6.04  5.1e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.132 on 38 degrees of freedom
## Multiple R-squared:  0.489,  Adjusted R-squared:  0.476 
## F-statistic: 36.4 on 1 and 38 DF,  p-value: 5.08e-07

Does the nitrogen concentration depend on the depth significantly?

(statistic <- (b[2] - 0) / sb2)                    
## [1] -6.036
# critical value
alpha <- 0.05
(K <- qt(1 - alpha/2, df=df))
## [1] 2.024
# p-value
(Pval <- 2 * pt(-abs(statistic), df = df))  # Is it correct and why?
## [1] 5.083e-07

What is our decision? Is the test from above somewhere here?

summary(fit1)   
## 
## Call:
## lm(formula = N ~ depth, data = peat, subset = (group == Group), 
##     x = TRUE)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.1949 -0.0923 -0.0196  0.0504  0.3437 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.16907    0.03819   30.61  < 2e-16 ***
## depth       -0.02755    0.00456   -6.04  5.1e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.132 on 38 degrees of freedom
## Multiple R-squared:  0.489,  Adjusted R-squared:  0.476 
## F-statistic: 36.4 on 1 and 38 DF,  p-value: 5.08e-07

Individual work

Additional material

In some situations (especially if there are lot of data points and no reasonable insight can be made by using a standard plot) a jittered version may be used instead. In this case the depth is randomly shifted by an amount from a uniform distribution on \([-0.5,+0.5]\).

set.seed(20010911)  
peat[, "jdepth"] <- peat[, "depth"] + runif(nrow(peat), -0.5, 0.5)
summary(peat)
##     group          N             depth           jdepth      
##  CB    :35   Min.   :0.499   Min.   : 0.00   Min.   :-0.461  
##  CB-VJJ:40   1st Qu.:0.899   1st Qu.: 4.00   1st Qu.: 3.814  
##  VJJ   :33   Median :1.034   Median : 8.00   Median : 7.850  
##  VJJ-CB:40   Mean   :1.077   Mean   : 7.53   Mean   : 7.489  
##              3rd Qu.:1.244   3rd Qu.:12.00   3rd Qu.:11.534  
##              Max.   :1.692   Max.   :14.00   Max.   :14.479

Another plot, this time with the jittered depth:

par(mfrow=c(1,1), mar=c(4,4,0.5,0.5))
plot(N ~ jdepth, data = peat, 
     xlab = XLAB, ylab = YLAB, xaxt = "n", 
     pch = PCH[group], col = COL[group], bg = BGC[group])
axis(1, at = seq(0, 14, by = 2))
abline(v = seq(1, 13, by = 2), col = "gray", lty = 5, lwd = 2)
legend(1.3, 1.7, legend = levels(peat[, "group"]), pch = PCH, col = COL,
       pt.bg = BGC, y.intersp = 1.2)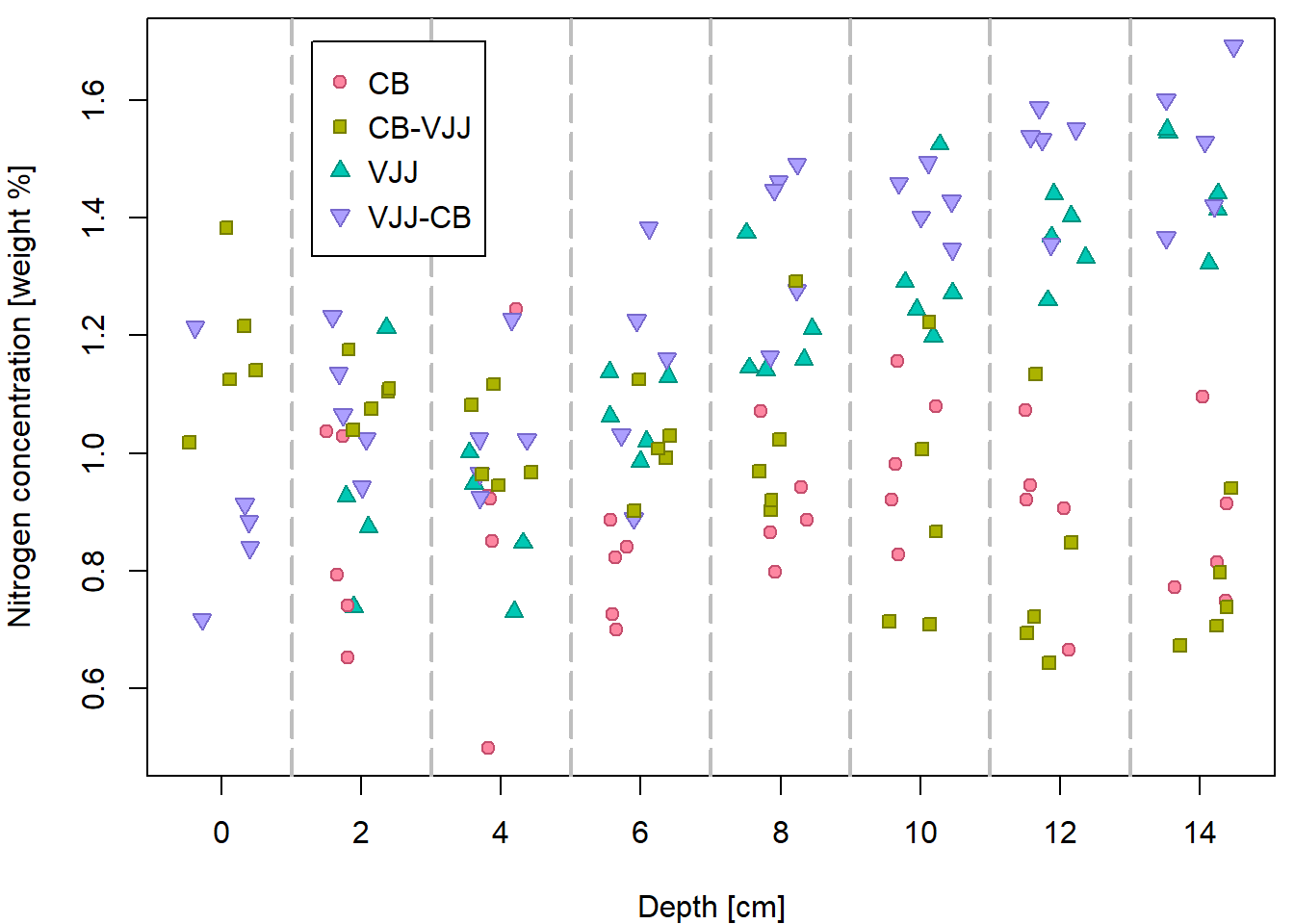

Similar plot using an R function jitter:

par(mfrow=c(1,1), mar=c(4,4,0.5,0.5))
plot(N ~ jitter(depth), data=peat, 
     xlab = XLAB, ylab = YLAB, 
     pch = PCH[group], col = COL[group], bg = BGC[group])