Model assumptions and graphical diagnostic tools
Jan Vávra
Exercise 7
Download this R markdown as: R, Rmd.
Outline of this lab session:
- Model assumptions and diagnostic tools
- Graphical diagnostic tools
Loading the data and libraries
Firstly, some necessary R libraries and the working dataset:
library("colorspace") # colors defined by function
library("mffSM") # data and plotLM()
library("splines") # B-splines modelling
library("MASS") # function stdres for standardized residualsWe are going to use the dataset Dris from the previous
exercise:
data(Dris, package = "mffSM")
# help("Dris")
head(Dris)## yield N P K Ca Mg
## 1 5.47 470 47 320 47 11
## 2 5.63 530 48 357 60 16
## 3 5.63 530 48 310 63 16
## 4 4.84 482 47 357 47 13
## 5 4.84 506 48 294 52 15
## 6 4.21 500 45 283 61 14summary(Dris)## yield N P K Ca Mg
## Min. :1.92 Min. :268 Min. :32.0 Min. :200 Min. :29.0 Min. : 8.0
## 1st Qu.:4.04 1st Qu.:427 1st Qu.:43.0 1st Qu.:338 1st Qu.:41.8 1st Qu.:10.0
## Median :4.84 Median :473 Median :49.0 Median :377 Median :49.0 Median :11.0
## Mean :4.86 Mean :470 Mean :48.6 Mean :375 Mean :51.5 Mean :11.6
## 3rd Qu.:5.56 3rd Qu.:518 3rd Qu.:54.0 3rd Qu.:407 3rd Qu.:59.0 3rd Qu.:13.0
## Max. :8.79 Max. :657 Max. :72.0 Max. :580 Max. :95.0 Max. :22.01. Basic model diagnostics
We will use the following model at the beginning:
aLogMg <- lm(yield ~ log2(Mg), data = Dris)
summary(aLogMg) ##
## Call:
## lm(formula = yield ~ log2(Mg), data = Dris)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.119 -0.741 -0.074 0.745 3.984
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.485 0.779 1.91 0.057 .
## log2(Mg) 0.961 0.221 4.35 1.8e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.07 on 366 degrees of freedom
## Multiple R-squared: 0.0491, Adjusted R-squared: 0.0465
## F-statistic: 18.9 on 1 and 366 DF, p-value: 1.77e-05We will closely inspect the model residuals. There are two types of residuals:
- Raw residuals \(u_1,
\dots, u_n\), that are supposed to satisfy:
- \(\mathsf{E}\, [u_i | \boldsymbol{X}_i] = 0\)
- \(\mathsf{var}\, [u_i | \boldsymbol{X}_i] = \sigma^2 m_{ii}\), where \(m_{ii}\) is a diagonal element of the matrix \(\mathbb{M} = (\mathbb{I} - \mathbb{H})\)
- in a normal linear model, it also holds that \(u_i\) follow the normal distribution, however, with different variance for different \(i \in \{1, \dots, n\}\)
- Standardized residuals \(v_i = u_i / \sqrt{MSe \times m_{ii}}\), for
\(i = 1, \dots, n\) that satify
- \(\mathsf{E}\, [v_i | \boldsymbol{X}_i] = 0\)
- \(\mathsf{var}\, [v_i | \boldsymbol{X}_i] = 1\)
- however, the standardized residuals are not normal – not even under the normal linear model
Here are the three most important nicely formatted graphical diagnostic tools:
par(mar = c(4,4,3,0.5))
plotLM(aLogMg) # function from 'mffSM' -1.png)
Individual work
How can we manually reconstruct the plots above?
- First plot (Residuals vs Fitted):
par(mfrow = c(1,2), mar = c(4,4,2,0.5))
plot(aLogMg, which = 1)
### manual computation
plot(fitted(aLogMg), residuals(aLogMg),
lwd=2, col="blue4", bg="skyblue", pch=21)
abline(h=0, col = "grey", lty = 3)
lines(lowess(fitted(aLogMg), residuals(aLogMg)), col="red", lwd=3)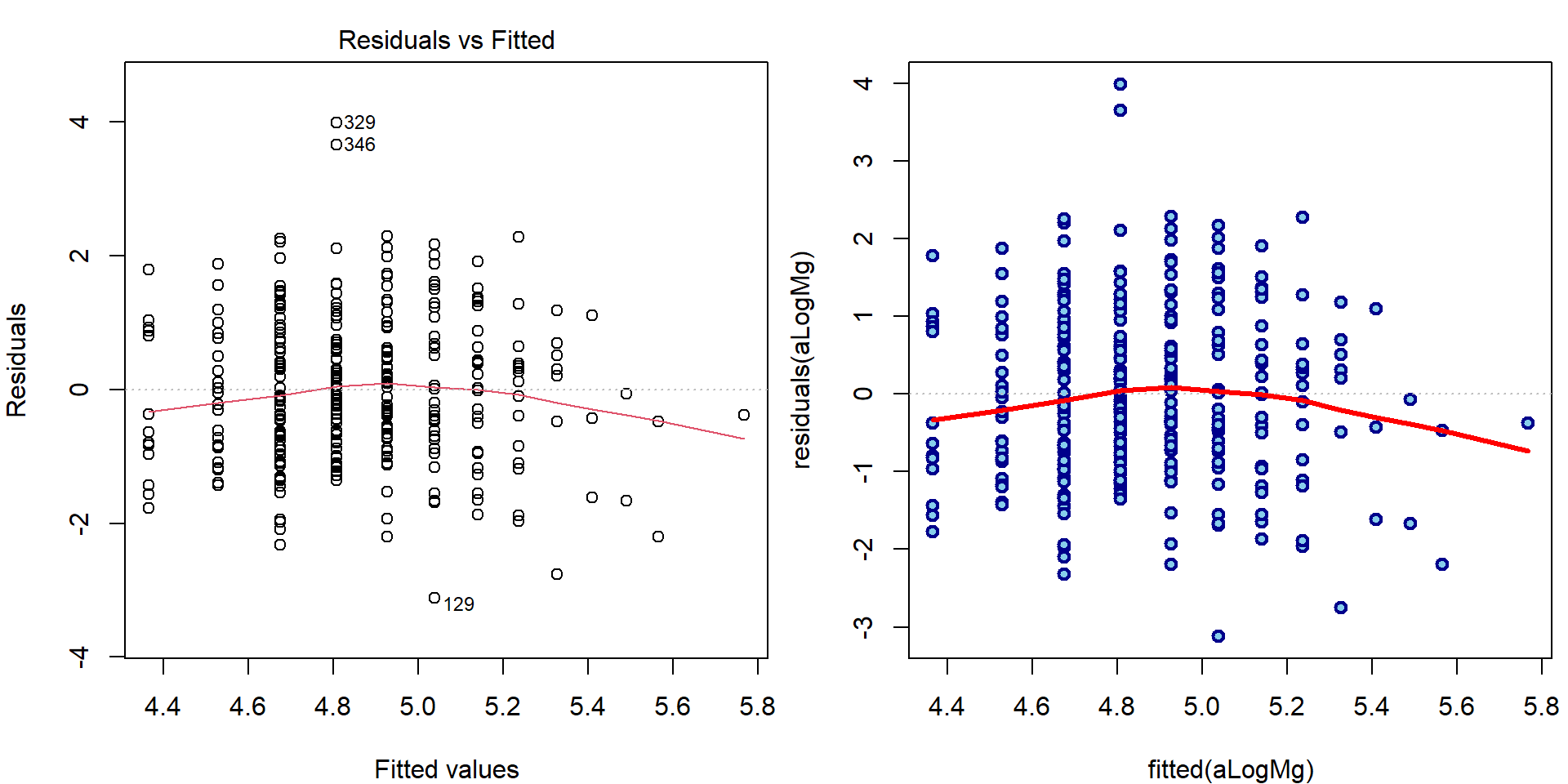
- Second plot (QQ plot):
par(mfrow = c(1,2), mar = c(4,4,2,0.5))
plot(aLogMg, which = 2, ask = FALSE)
### standardized residuals
H = qr.Q(aLogMg[["qr"]]) %*% t(qr.Q(aLogMg[["qr"]]))
M = diag(nrow(H))-H
stdres = residuals(aLogMg)/sqrt(deviance(aLogMg)/aLogMg$df.residual*diag(M))
qq = qqnorm(stdres, plot.it=FALSE)
# all.equal(stdres(aLogMg), stdres) # --> TRUE (computed by MASS function)
# all.equal(qq$y, stdres) # --> TRUE (will be on y-axis)
plot(qq$x, qq$y, lwd=2, col="blue4", bg="skyblue", pch=21)
qqline(stdres, lwd=2, lty=3)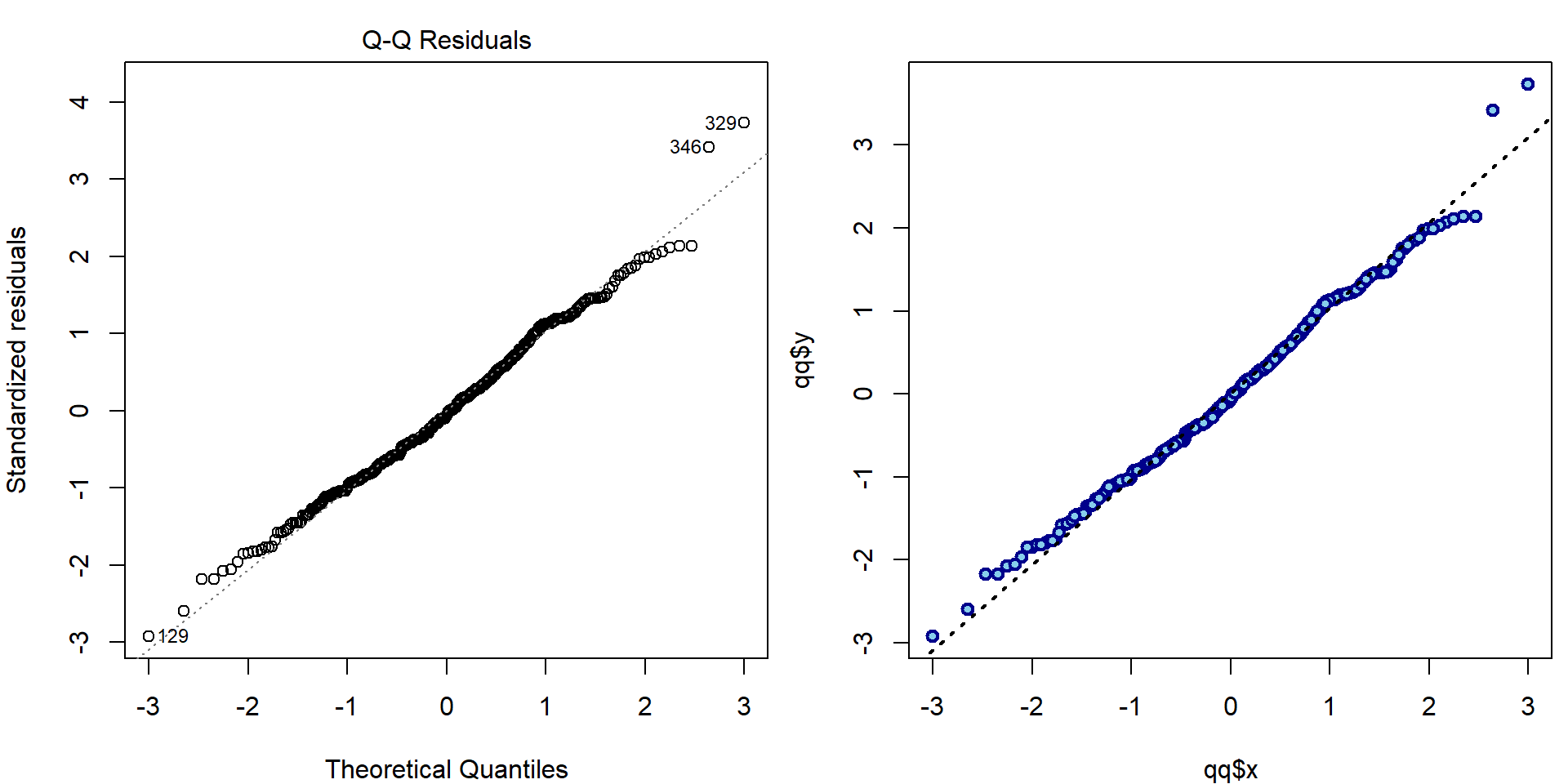
- Third plot (Scale-Location plot)
par(mfrow = c(1,2), mar = c(4,4,2,0.5))
plot(aLogMg, which = 3, ask = FALSE)
### manual computation
plot(fitted(aLogMg), sqrt(abs(stdres)),
lwd=2, col="blue4", bg="skyblue", pch=21)
lines(lowess(fitted(aLogMg), sqrt(abs(stdres))), col="red", lwd=3)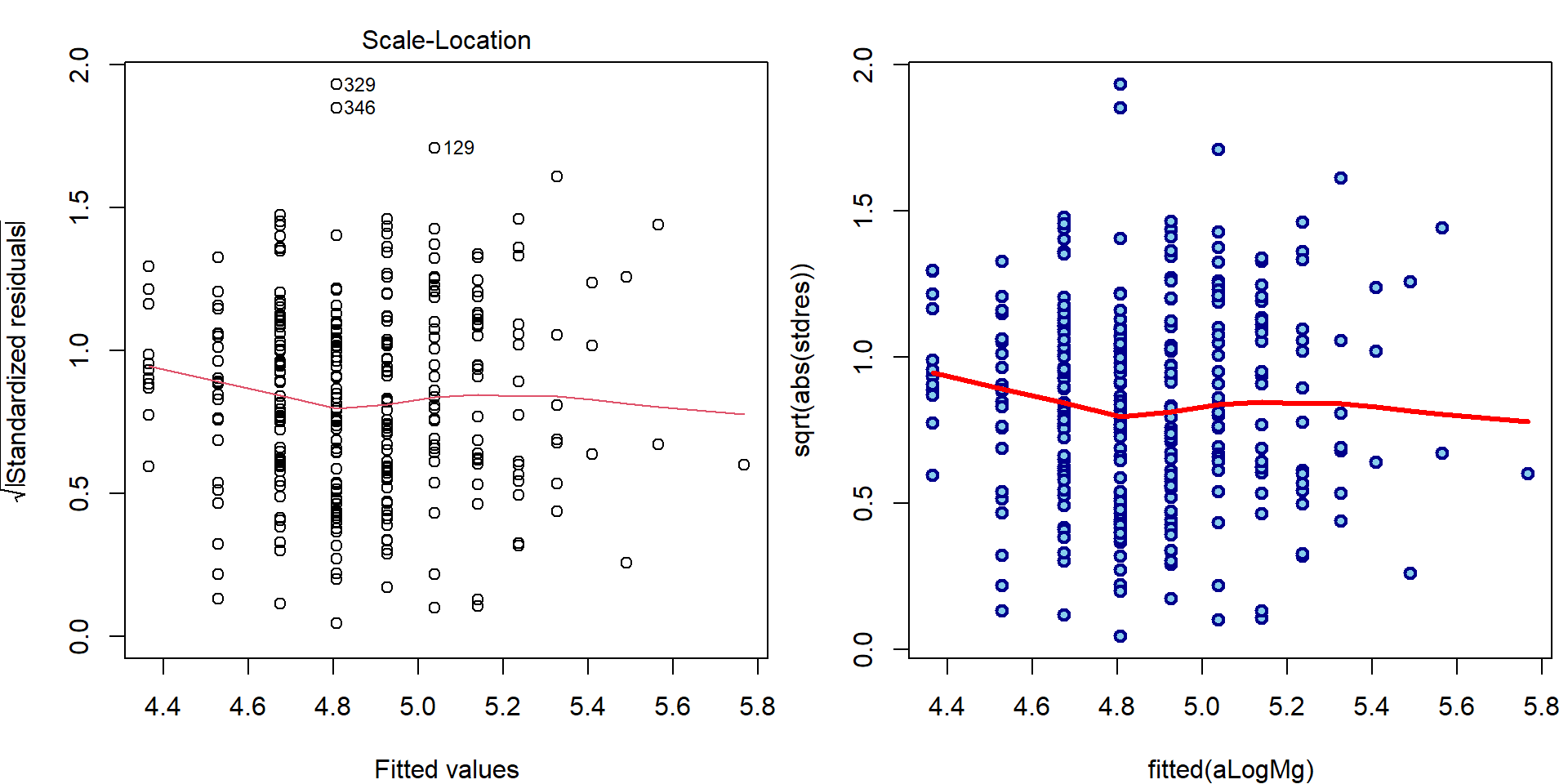
Note, that there are actually infinitely many possibilities how to check that \(\mathsf{E}\,(u_i| \boldsymbol{X}_i) = 0\). A scatterplot of fitted values vs. residuals is only one of them. Other common possibility is to plot the covariate values vs. the residuals.
par(mfrow = c(1,2), mar = c(4,4,2,0.5))
plot(log2(Dris$Mg), residuals(aLogMg),
xlab=expression(log[2](Mg)), ylab="Residuals",
main="Residuals vs. covariate in model",
pch = 21, col = "blue4", bg = "skyblue")
lines(lowess(residuals(aLogMg)~log2(Dris$Mg)), col="red")
plot(log2(Dris$Ca), residuals(aLogMg),
xlab=expression(log[2](Ca)), ylab="Residuals",
main="Residuals vs. covariate not in model",
pch = 21, col = "blue4", bg = "skyblue")
lines(lowess(residuals(aLogMg)~log2(Dris$Ca)), col="red")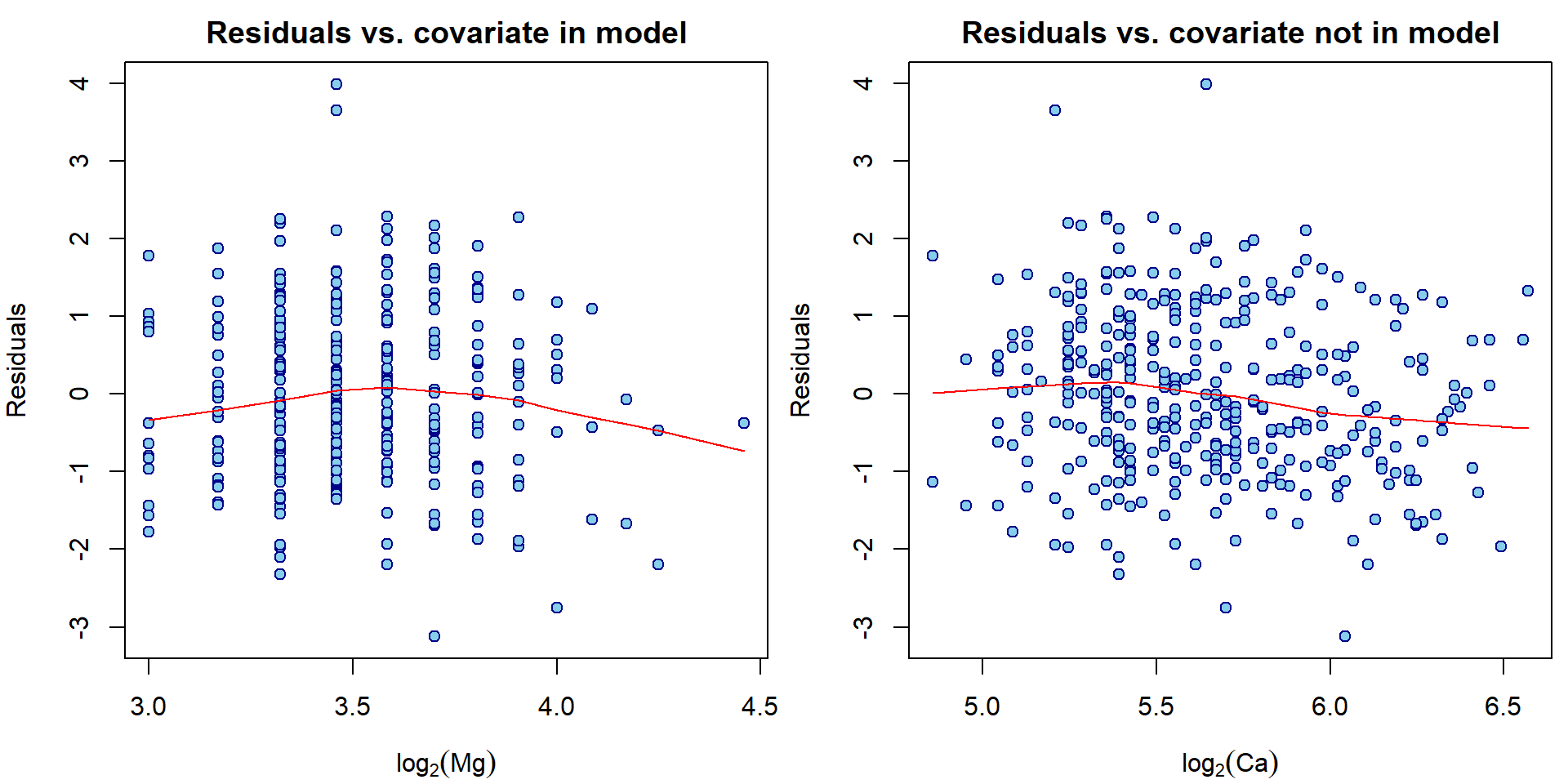
Also check the following and explain the results:
sum(aLogMg$residuals)## [1] -5.523e-14sum(aLogMg$residuals*log2(Dris$Mg))## [1] -2.583e-13Compare the plots for model aLogMg with the interaction
model from previous exercise:
par(mar = c(4,4,3,0.5))
plotLM(lm(yield ~ log2(Mg) + log2(Ca) + I(log2(Mg) * log2(Ca)), data = Dris))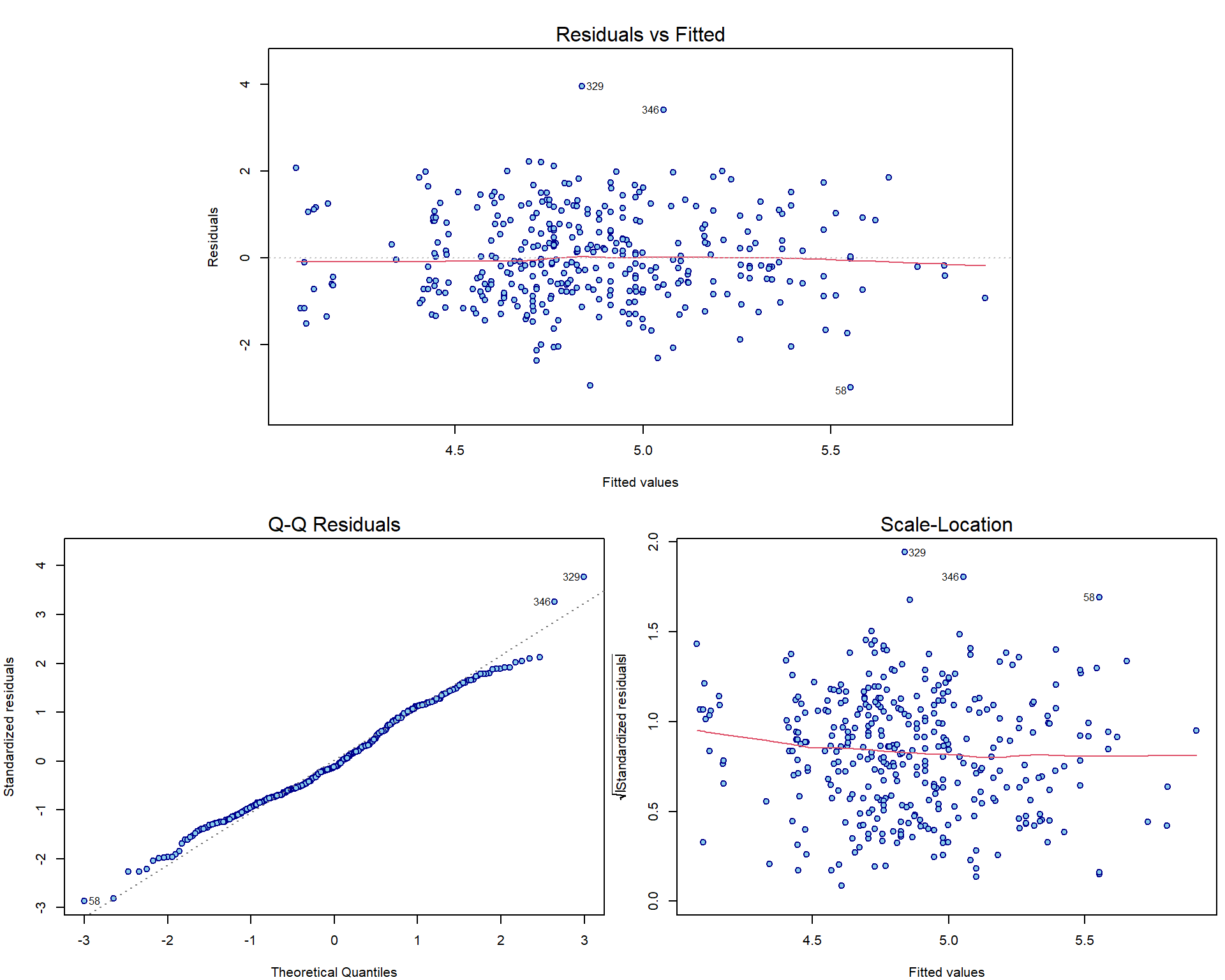
2. Polynomials and splines as regressors
For some example of possible model improvements, we will consider a different dataset. We will fit a series of different models that we will mutually compare.
A dataset providing a series of (independent) measurements of head
acceleration in a simulated motorcycle accident (used to test crash
helmets) is given in the datafile Motorcycle (within the R
package mffSM).
data(Motorcycle, package = "mffSM")
# help(Motorcycle)
head(Motorcycle)## time haccel
## 1 2.4 0.0
## 2 2.6 -1.3
## 3 3.2 -2.7
## 4 3.6 0.0
## 5 4.0 -2.7
## 6 6.2 -2.7dim(Motorcycle)## [1] 133 2summary(Motorcycle)## time haccel
## Min. : 2.4 Min. :-134.0
## 1st Qu.:15.8 1st Qu.: -54.9
## Median :24.0 Median : -13.3
## Mean :25.6 Mean : -25.6
## 3rd Qu.:35.2 3rd Qu.: 0.0
## Max. :65.6 Max. : 75.0We are primarily interested in how the head acceleration (covariate
haccel) depends on the time after the accident (given in
miliseconds – the time covariate).
par(mfrow = c(1,1), mar = c(4,4,1,1))
plot(haccel ~ time, data = Motorcycle, pch = 21, bg = "orange", col = "red3",
xlab = "Time [ms]", ylab = "Head acceleration [g]")
fit0 = lm(haccel~time, data=Motorcycle)
abline(fit0)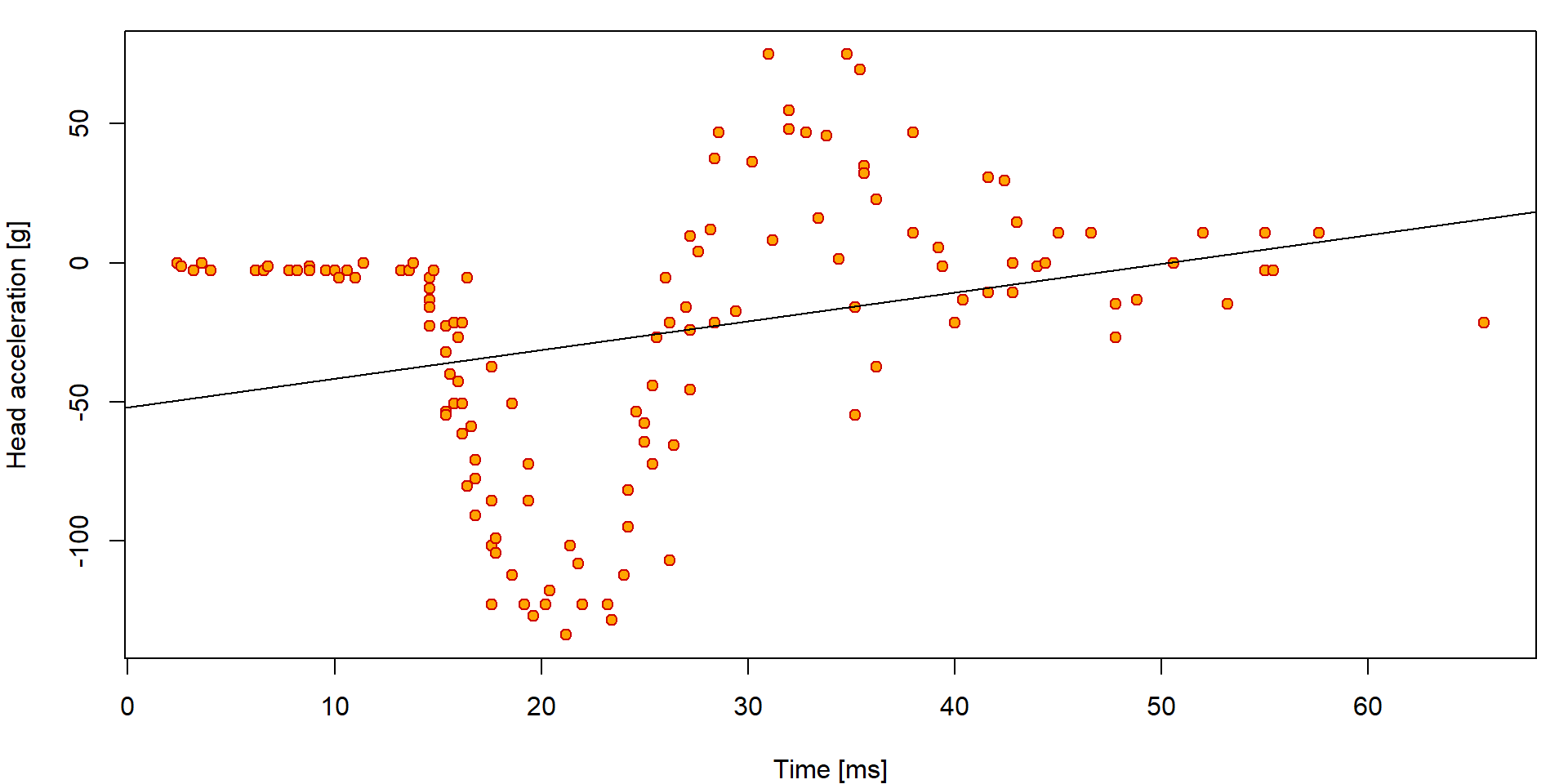
Using the diagnostic plots, we can clearly see that the model denoted
as fit0 is hardly appropriate:
par(mar = c(4,4,3,0.5))
plotLM(fit0)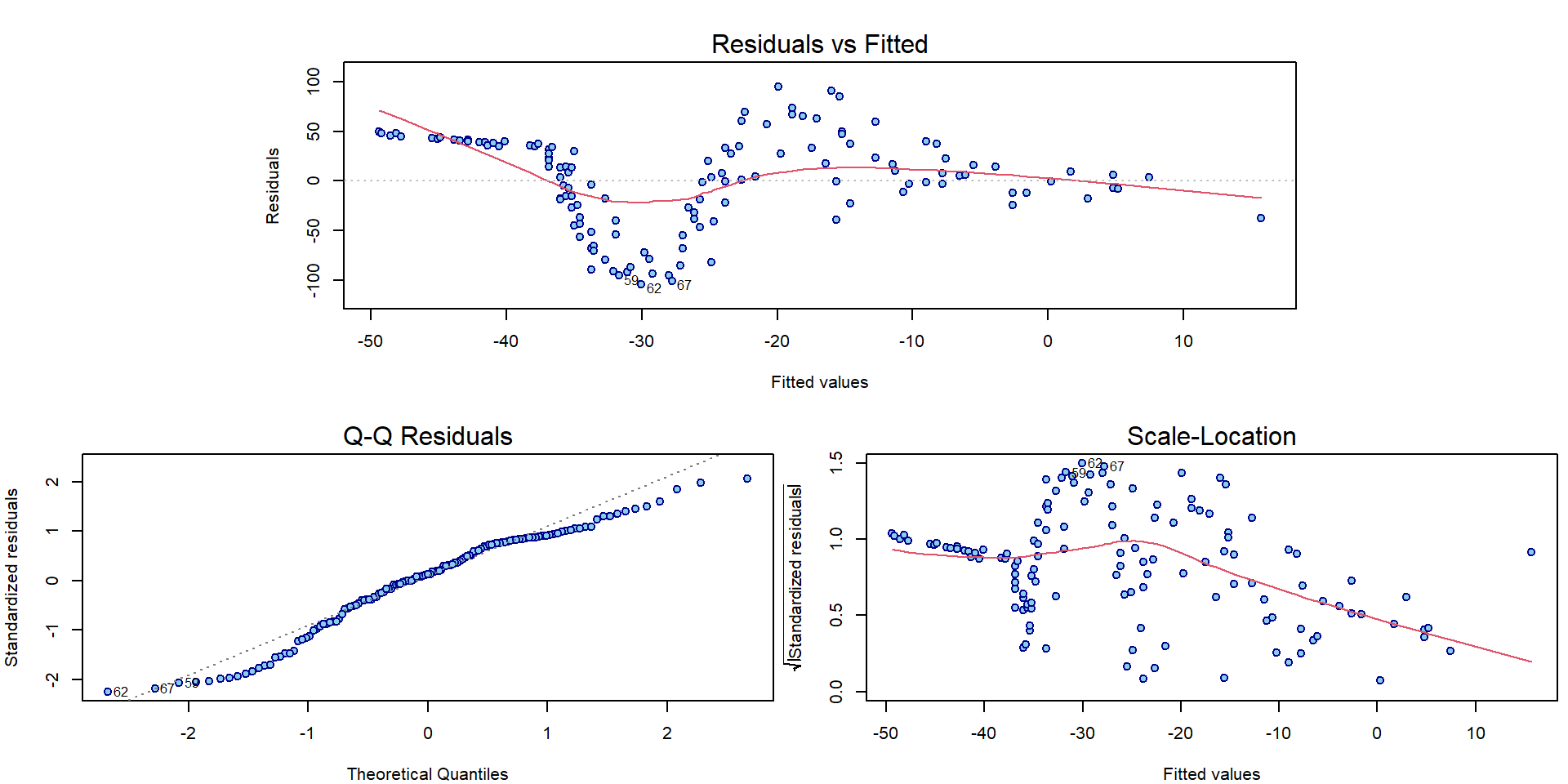
As far as there is a quite flexible shape observed in the plot we need some more flexible model to capture the structure of the underlying conditional expectation of the head acceleration given the time. We will use polynomials (of different degrees) for fitting the model (while still staying within the linear regression framework).
fit6 <- lm(haccel~poly(time, 6, raw=TRUE), data=Motorcycle)
fit12 <- lm(haccel~poly(time, 12, raw=TRUE), data=Motorcycle)The model can be visualized as follows:
xgrid <- seq(0, 70, length = 500)
par(mfrow = c(1,1), mar = c(4,4,2,1))
plot(haccel ~ time, data = Motorcycle, pch = 21, bg = "orange", col = "red3",
main = "Fitted polynomial curves",
xlab = "Time [ms]", ylab = "Head acceleration [g]")
lines(xgrid, predict(fit6, newdata=data.frame(time=xgrid)), lwd=2, col="blue")
lines(xgrid, predict(fit12, newdata=data.frame(time=xgrid)), lwd=2, col="darkgreen")
legend(37,-70, lty=rep(1, 2), col=c("blue", "darkgreen"),
legend=paste("p=", c(6,12),sep=""), lwd=c(2,2), cex=1.2)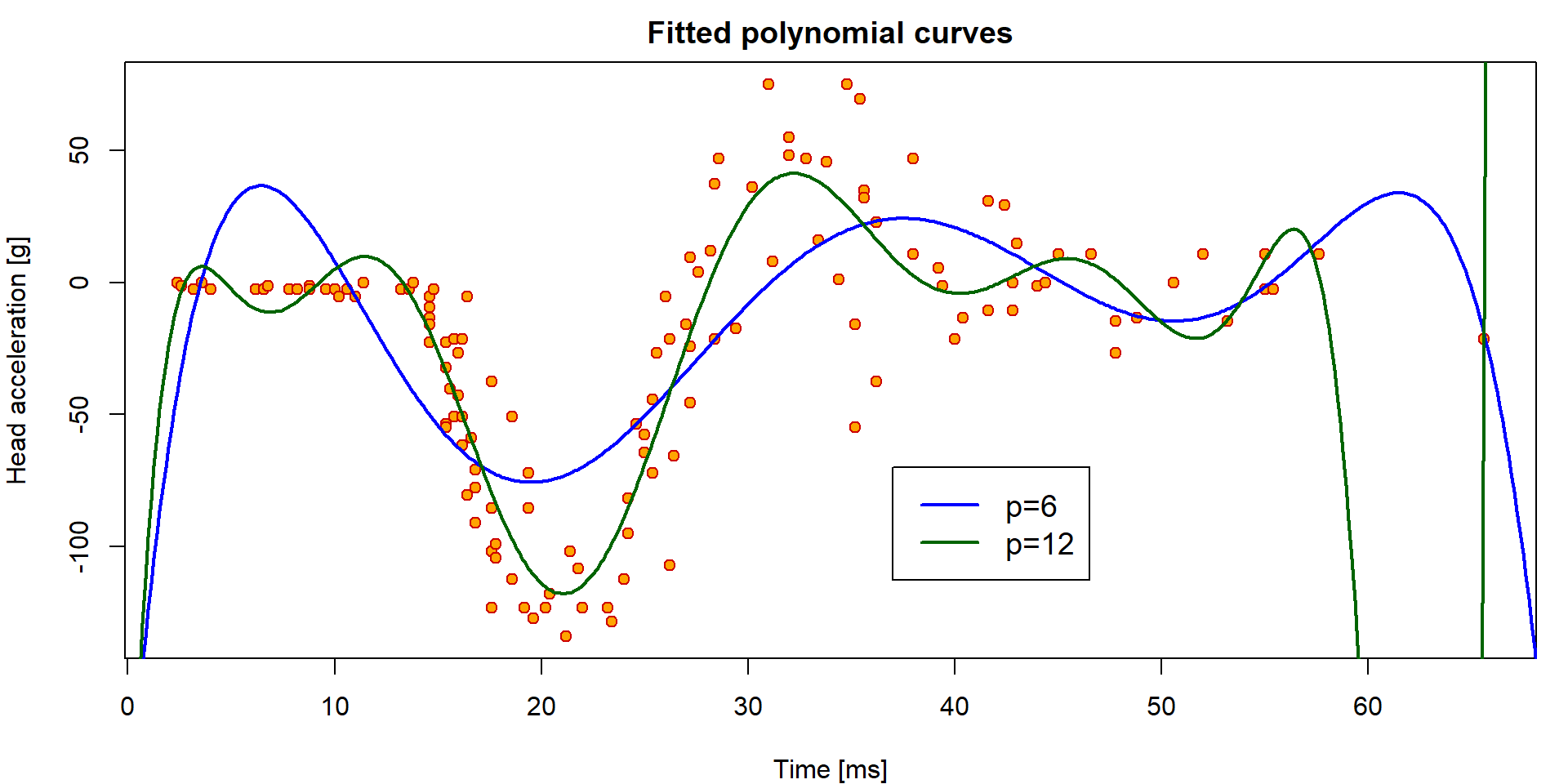
Classical polynomials are, however, not computationally very
effective. Especially for higher order of the polynomial approximation
the solution tends to be unstable. To avoid numerical problems you can
use orthogonal polynomials with raw=FALSE, which stabilizes
the magnitude (and standard errors) of estimated coefficients:
summary(fit6)##
## Call:
## lm(formula = haccel ~ poly(time, 6, raw = TRUE), data = Motorcycle)
##
## Residuals:
## Min 1Q Median 3Q Max
## -76.0 -23.6 -0.5 24.0 75.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.07e+02 4.35e+01 -4.76 5.3e-06 ***
## poly(time, 6, raw = TRUE)1 9.66e+01 1.56e+01 6.20 7.5e-09 ***
## poly(time, 6, raw = TRUE)2 -1.30e+01 1.86e+00 -6.98 1.5e-10 ***
## poly(time, 6, raw = TRUE)3 7.16e-01 1.01e-01 7.08 9.0e-11 ***
## poly(time, 6, raw = TRUE)4 -1.87e-02 2.73e-03 -6.85 3.0e-10 ***
## poly(time, 6, raw = TRUE)5 2.32e-04 3.57e-05 6.50 1.7e-09 ***
## poly(time, 6, raw = TRUE)6 -1.10e-06 1.80e-07 -6.13 1.1e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 33.1 on 126 degrees of freedom
## Multiple R-squared: 0.552, Adjusted R-squared: 0.531
## F-statistic: 25.9 on 6 and 126 DF, p-value: <2e-16summary(lm(haccel~poly(time, 6, raw=FALSE), data=Motorcycle))##
## Call:
## lm(formula = haccel ~ poly(time, 6, raw = FALSE), data = Motorcycle)
##
## Residuals:
## Min 1Q Median 3Q Max
## -76.0 -23.6 -0.5 24.0 75.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -25.55 2.87 -8.90 5.0e-15 ***
## poly(time, 6, raw = FALSE)1 160.61 33.09 4.85 3.5e-06 ***
## poly(time, 6, raw = FALSE)2 99.01 33.09 2.99 0.0033 **
## poly(time, 6, raw = FALSE)3 -244.97 33.09 -7.40 1.7e-11 ***
## poly(time, 6, raw = FALSE)4 64.68 33.09 1.95 0.0528 .
## poly(time, 6, raw = FALSE)5 171.29 33.09 5.18 8.7e-07 ***
## poly(time, 6, raw = FALSE)6 -202.78 33.09 -6.13 1.1e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 33.1 on 126 degrees of freedom
## Multiple R-squared: 0.552, Adjusted R-squared: 0.531
## F-statistic: 25.9 on 6 and 126 DF, p-value: <2e-16Another possible solution how to introduce some reasonable stability into the model where some higher order polynomials are used, are splines.
### Choice of knots
knots <- c(0, 11, 12, 13, 20, 30, 32, 34, 40, 50, 70)
(inner <- knots[-c(1, length(knots))]) # inner knots ## [1] 11 12 13 20 30 32 34 40 50(bound <- knots[c(1, length(knots))]) # boundary knots ## [1] 0 70### B-splines of degree 3
DEGREE <- 3 # piecewise cubic
Bgrid <- bs(xgrid, knots = inner, Boundary.knots = bound, degree = DEGREE,
intercept = TRUE)
dim(Bgrid) # 13-dimensional linear space of piecewise polynomials## [1] 500 13The B-spline basis is a set of the following functions:
COL <- rainbow_hcl(ncol(Bgrid), c = 80)
par(mfrow = c(1,1), mar = c(4,4,1,1))
plot(xgrid, Bgrid[,1], type = "l", col = COL[1], lwd = 2, xlab = "x",
ylab = "B(x)", xlim = range(knots), ylim = range(Bgrid, na.rm = TRUE))
for (j in 2:ncol(Bgrid)) lines(xgrid, Bgrid[,j], col = COL[j], lwd = 2)
points(knots, rep(0, length(knots)),
pch = 21, bg = "blue", col = "skyblue", cex = 1.5)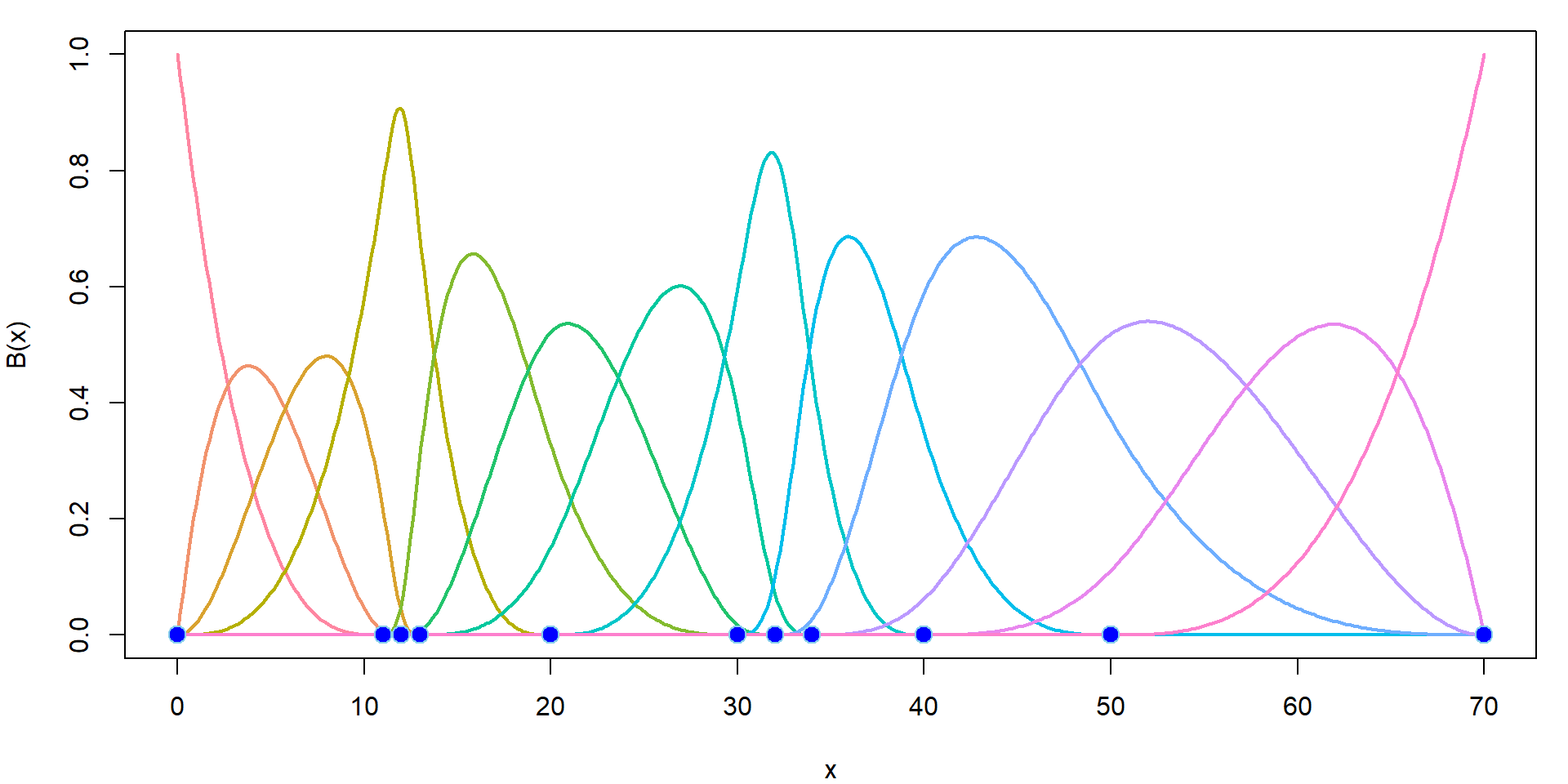
Thus, we can use B-splines to fit the model.
More details about the B-splines can be found, for instance, here.
m1 <- lm(haccel ~ bs(time, knots = inner, Boundary.knots = bound,
degree = DEGREE, intercept = TRUE) - 1, data = Motorcycle)This is the fitted curve:
par(mfrow = c(1,1), mar = c(4,4,2,1))
plot(haccel ~ time, data = Motorcycle, pch = 21, bg = "orange", col = "red3",
main = "Fitted B-spline curve",
xlab = "Time [ms]", ylab = "Head acceleration [g]")
lines(xgrid, predict(m1, newdata=data.frame(time=xgrid)), lwd=2, col="blue")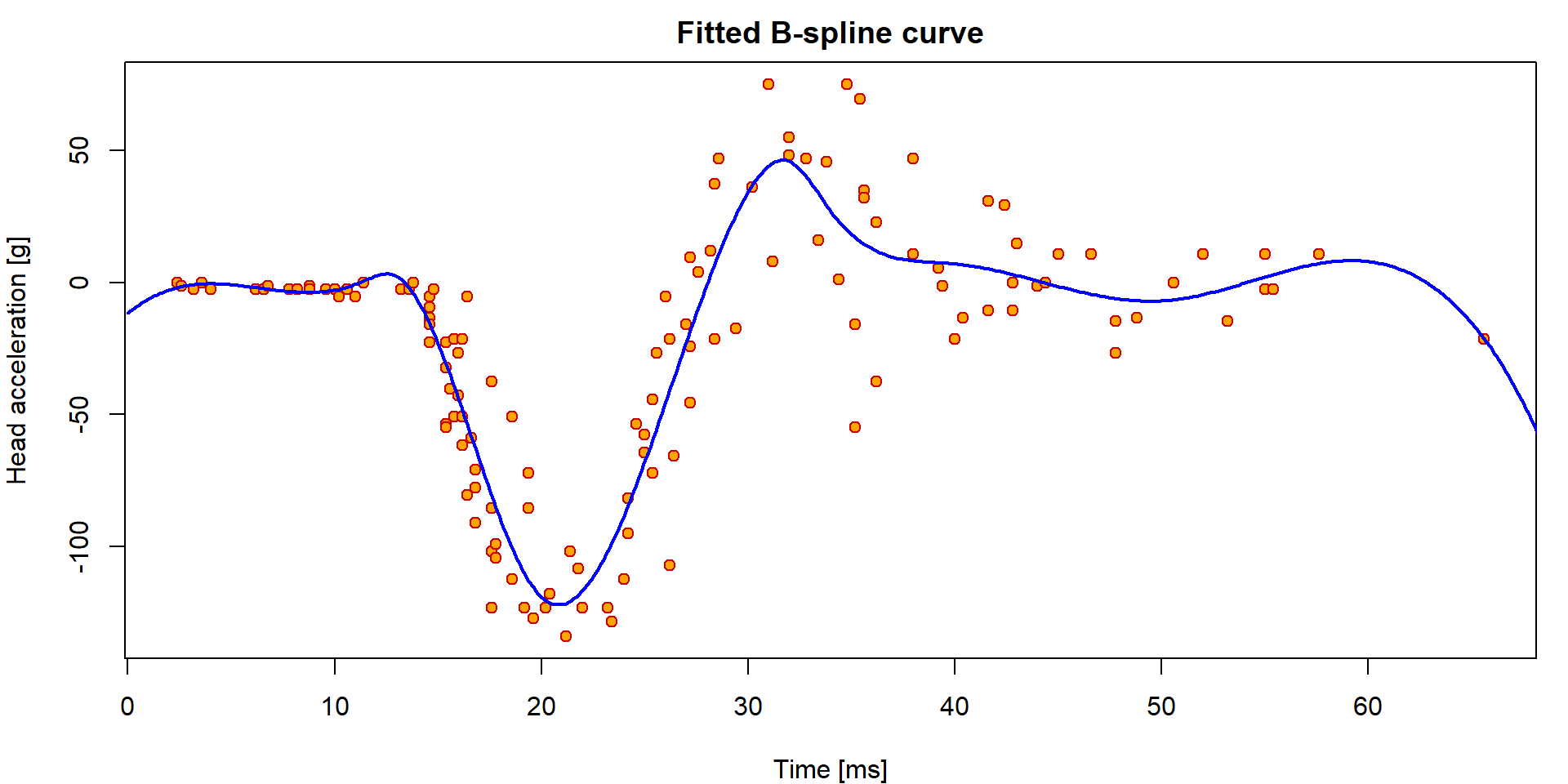
names(m1$coefficients) <- paste("B", 1:ncol(Bgrid))
summary(m1)##
## Call:
## lm(formula = haccel ~ bs(time, knots = inner, Boundary.knots = bound,
## degree = DEGREE, intercept = TRUE) - 1, data = Motorcycle)
##
## Residuals:
## Min 1Q Median 3Q Max
## -71.86 -11.74 -0.27 10.36 55.25
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## B 1 -11.61 83.25 -0.14 0.89
## B 2 12.45 81.28 0.15 0.88
## B 3 -13.99 45.35 -0.31 0.76
## B 4 2.98 18.89 0.16 0.87
## B 5 6.11 12.14 0.50 0.62
## B 6 -237.28 18.85 -12.59 < 2e-16 ***
## B 7 17.35 14.09 1.23 0.22
## B 8 53.25 12.63 4.21 4.9e-05 ***
## B 9 5.10 13.05 0.39 0.70
## B 10 12.61 17.15 0.74 0.46
## B 11 -34.95 38.16 -0.92 0.36
## B 12 58.26 65.05 0.90 0.37
## B 13 -93.07 75.92 -1.23 0.22
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 22.6 on 120 degrees of freedom
## Multiple R-squared: 0.845, Adjusted R-squared: 0.828
## F-statistic: 50.2 on 13 and 120 DF, p-value: <2e-16Since the intercept is included within the B-spline basis
(intercept = TRUE in bs), we omitted it in the
formula with -1. However, this use comes with some issues
deeply rooted within the implementation. For example, neither
Multiple R-squared nor the F-statistic
quantity in the output correspond to correct numbers. Simply put,
summary.lm thinks the intercept is not included despite
still being a linear combination of given columns.
Individual work
Can you explain why the values reported for \(R^2\) and \(R_{adj}^2\) are not appropriate? What is the right meaning of these numbers? Can you manually reconstruct them?
The \(R^2\) value from the model is
summary(m1)$r.squared## [1] 0.8447and the manual calculations will give
1 - deviance(m1)/sum(Motorcycle$haccel^2)## [1] 0.8447sum(fitted(m1)^2)/sum(Motorcycle$haccel^2)## [1] 0.8447Interpretation of the F-test from the summary output above is a test of a submodel
summary(m1)$fstatistic## value numdf dendf
## 50.19 13.00 120.00# the usual F-test (correct)
m2 <- lm(haccel ~ 1, data = Motorcycle)
anova(m2, m1)## Analysis of Variance Table
##
## Model 1: haccel ~ 1
## Model 2: haccel ~ bs(time, knots = inner, Boundary.knots = bound, degree = DEGREE,
## intercept = TRUE) - 1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 132 308223
## 2 120 61362 12 246861 40.2 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# the wrong F-test (in summary m1)
(m0 <- lm(haccel ~ -1, data=Motorcycle))##
## Call:
## lm(formula = haccel ~ -1, data = Motorcycle)
##
## No coefficientsanova(m0 ,m1)## Analysis of Variance Table
##
## Model 1: haccel ~ -1
## Model 2: haccel ~ bs(time, knots = inner, Boundary.knots = bound, degree = DEGREE,
## intercept = TRUE) - 1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 133 395017
## 2 120 61362 13 333655 50.2 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Nevertheless, as the intercept parameter is in the linear span of the columns of \(\mathbb{X}\), it makes sense to calculate the (usual) multiple \(R^2\) value. This can be done ‘manually’ as follows:
var(fitted(m1)) / var(Motorcycle$haccel)## [1] 0.8009cor(Motorcycle$haccel, fitted(m1))^2## [1] 0.80091 - deviance(m1)/deviance(m2)## [1] 0.8009Alternatively, one can use B-splines (the basis without intercept) with an intercept in the model to get some meaningful numbers in the output:
m0 <- lm(haccel ~ bs(time, knots = inner, Boundary.knots = bound,
degree = DEGREE, intercept = FALSE), data = Motorcycle)
names(m0$coefficients) <- c("(Intercept)", paste("B", 1:12))
summary(m0)##
## Call:
## lm(formula = haccel ~ bs(time, knots = inner, Boundary.knots = bound,
## degree = DEGREE, intercept = FALSE), data = Motorcycle)
##
## Residuals:
## Min 1Q Median 3Q Max
## -71.86 -11.74 -0.27 10.36 55.25
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -11.61 83.25 -0.14 0.889
## B 1 24.06 161.97 0.15 0.882
## B 2 -2.37 57.84 -0.04 0.967
## B 3 14.60 93.33 0.16 0.876
## B 4 17.73 80.50 0.22 0.826
## B 5 -225.67 88.70 -2.54 0.012 *
## B 6 28.96 82.78 0.35 0.727
## B 7 64.86 84.77 0.77 0.446
## B 8 16.72 84.00 0.20 0.843
## B 9 24.22 85.17 0.28 0.777
## B 10 -23.33 91.34 -0.26 0.799
## B 11 69.87 105.92 0.66 0.511
## B 12 -81.45 112.46 -0.72 0.470
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 22.6 on 120 degrees of freedom
## Multiple R-squared: 0.801, Adjusted R-squared: 0.781
## F-statistic: 40.2 on 12 and 120 DF, p-value: <2e-16anova(m2,m0)## Analysis of Variance Table
##
## Model 1: haccel ~ 1
## Model 2: haccel ~ bs(time, knots = inner, Boundary.knots = bound, degree = DEGREE,
## intercept = FALSE)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 132 308223
## 2 120 61362 12 246861 40.2 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1What about the interpretation of the classical diagnostic plots for the model fitted with B-splines?
par(mar = c(4,4,3,0.5))
plotLM(m1)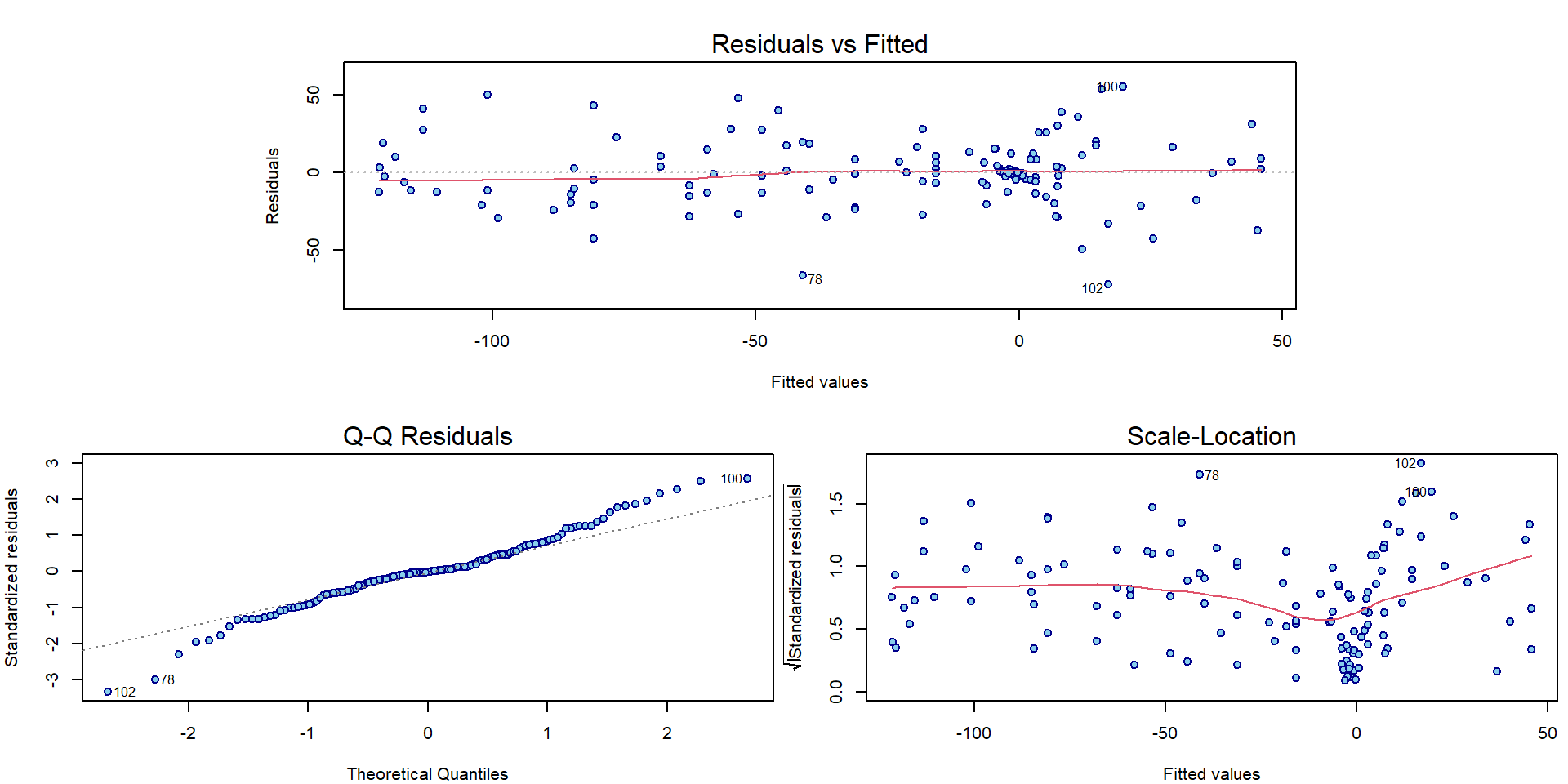
It seems there is some issue with homoscedasticity assumption. Let’s change the x-axis of the third Scale-Location plot to determine how the variability changes:
par(mfrow = c(1,2), mar = c(4,4,2,1))
plot(abs(fitted(m1)), sqrt(abs(stdres(m1))),
main = "Abs(fitted)",
lwd=2, col="blue4", bg="skyblue", pch=21)
lines(lowess(abs(fitted(m1)), sqrt(abs(stdres(m1)))), col="red", lwd=3)
plot(Motorcycle$time, sqrt(abs(stdres(m1))),
main = "Time",
lwd=2, col="blue4", bg="skyblue", pch=21)
lines(lowess(Motorcycle$time, sqrt(abs(stdres(m1)))), col="red", lwd=3)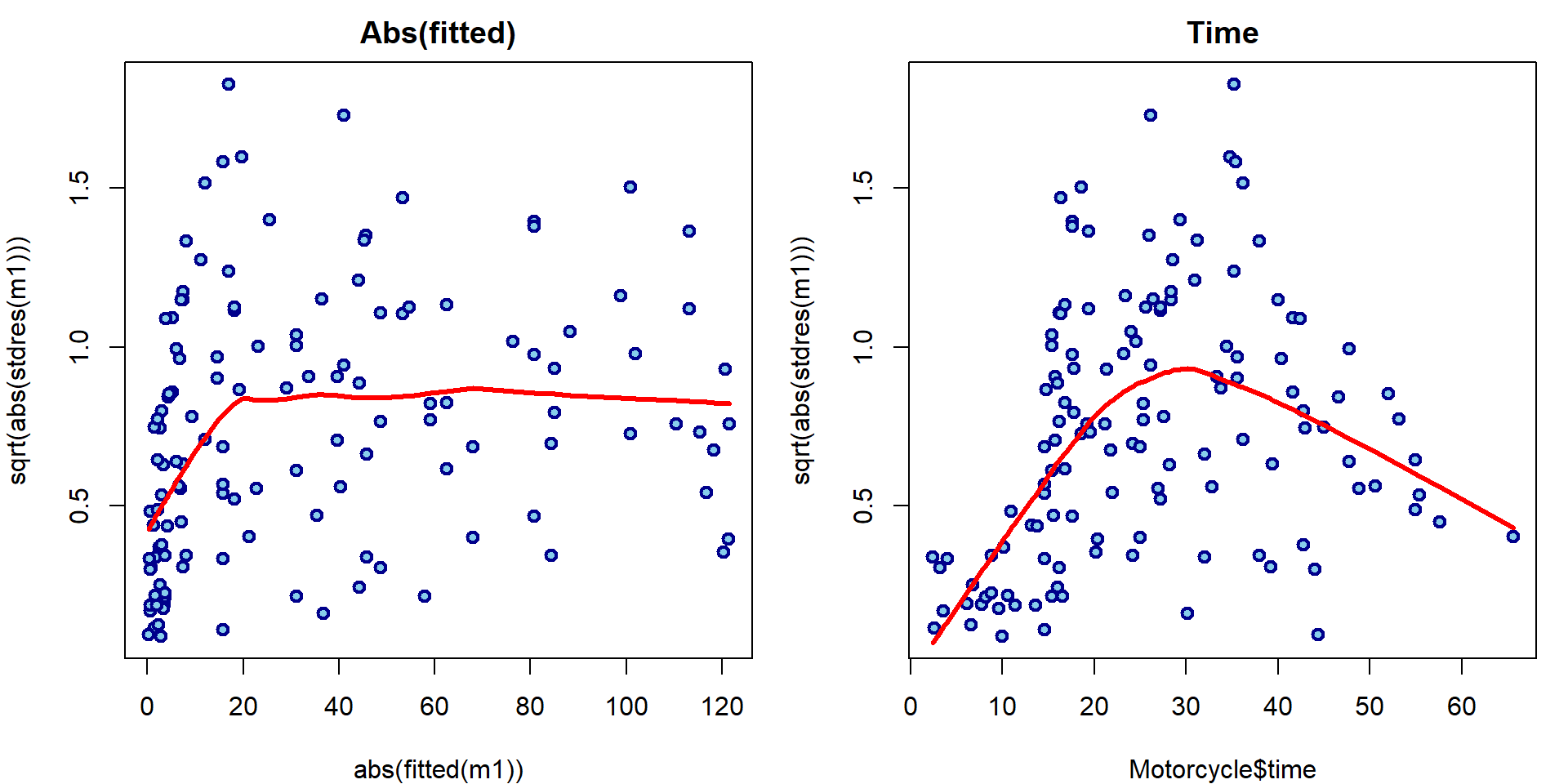
How to adjust the inference for heteroscedastic models will be shown later.