Log-transformation of the response
Jan Vávra
Exercise 9
Download this R markdown as: R, Rmd.
Outline of this lab session:
- Homoscedastic vs. heteroscedastic data/model
- Logarithmic transformation of the response
- Regression planes
Loading the data and libraries
We will use a small dataset (47 observations and 8 different covariates) containing some pieces of information about fires that occurred in Chicago in 1970 while distinguishing for some information provided in the data. Particularly, we will focus on the locality in Chicago (north vs. south) and the proportion of minority citizens. The dataset is loaded from the website and some brief insight is provided below.
library("mffSM") # plotLM()
library("MASS") # stdres()
library("fBasics") # dagoTest()
library("car") # ncvTest()
library("lmtest") # bptest()
chicago <- read.csv("http://www.karlin.mff.cuni.cz/~vavraj/nmfm334/data/chicago.csv",
header=T, stringsAsFactors = TRUE)
chicago <- transform(chicago,
fside = factor(side, levels = 0:1, labels=c("North", "South")))
head(chicago)## minor fire theft old insur income side fside
## 1 10.0 6.2 29 60.4 0.0 11.744 0 North
## 2 22.2 9.5 44 76.5 0.1 9.323 0 North
## 3 19.6 10.5 36 73.5 1.2 9.948 0 North
## 4 17.3 7.7 37 66.9 0.5 10.656 0 North
## 5 24.5 8.6 53 81.4 0.7 9.730 0 North
## 6 54.0 34.1 68 52.6 0.3 8.231 0 Northsummary(chicago)## minor fire theft old insur income
## Min. : 1.00 Min. : 2.00 Min. : 3.0 Min. : 2.0 Min. :0.000 Min. : 5.58
## 1st Qu.: 3.75 1st Qu.: 5.65 1st Qu.: 22.0 1st Qu.:48.6 1st Qu.:0.000 1st Qu.: 8.45
## Median :24.50 Median :10.40 Median : 29.0 Median :65.0 Median :0.400 Median :10.69
## Mean :34.99 Mean :12.28 Mean : 32.4 Mean :60.3 Mean :0.615 Mean :10.70
## 3rd Qu.:57.65 3rd Qu.:16.05 3rd Qu.: 38.0 3rd Qu.:77.3 3rd Qu.:0.900 3rd Qu.:11.99
## Max. :99.70 Max. :39.70 Max. :147.0 Max. :90.1 Max. :2.200 Max. :21.48
## side fside
## Min. :0.000 North:25
## 1st Qu.:0.000 South:22
## Median :0.000
## Mean :0.468
## 3rd Qu.:1.000
## Max. :1.000The data contain information from Chicago insurance redlining in 47 districts in 1970 where
minorstands for the percentage of minority (0 - 100) in a given district,firestands for the number of fires per 100 households during the reference period,theftdenotes the number of reported thefts per 1000 inhabitants,oldgives percentage of residential units built before 1939,insurstates the number of policies per 100 household,incomeis the median income (USD 1000) per household,sidegives the location of the district within Chicago (0 = North, 1 = South).
Individual work
Use the data on fires in Chicago (the dataset loaded above) and
perform some basic explanatory analysis while focusing on the number of
fires (the dependent variable fire and two explanatory
variables the proportion of the minority (minor) and the
location in Chicago (side).
What are you expectations about the form of the regression function when being interested in modeling of the conditional number of fires \(\mathsf{E} [Y |\, \mathtt{minor}, \mathtt{side}]\), while conditioning on the minority proportion and the locality information?
Are there some issues that you should be concern with? What about the assumptions on normal regression model or an ordinary regression model (without the assumption of normality)?
What particular graphical tools can be used to visually verify the assumptions imposed on the model?
1. Expected number of fires given minority and locality
We start by looking for a model of dependence of the number of fires
(fire) on the percentage of minority (minor).
We are also aware of the fact that the form of this dependence may
differ in north and south parts of Chicago.
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
XLAB <- "Minority (%)"
YLAB <- "Fires (#/100 households)"
COLS <- c(North = "darkgreen", South = "red")
BGS <- c(North = "aquamarine", South = "orange")
PCHS <- c(North = 21, South = 23)
plot(fire ~ minor, data = chicago,
xlab = XLAB, ylab = YLAB,
col = COLS[fside], bg = BGS[fside], pch = PCHS[fside])
legend("topleft", legend = c("North", "South"), bty = "n",
pch = PCHS, col = COLS, pt.bg = BGS)
lines(with(subset(chicago, fside == "North"), lowess(minor, fire)),
col = COLS["North"], lwd = 2)
lines(with(subset(chicago, fside == "South"), lowess(minor, fire)),
col = COLS["South"], lwd = 2)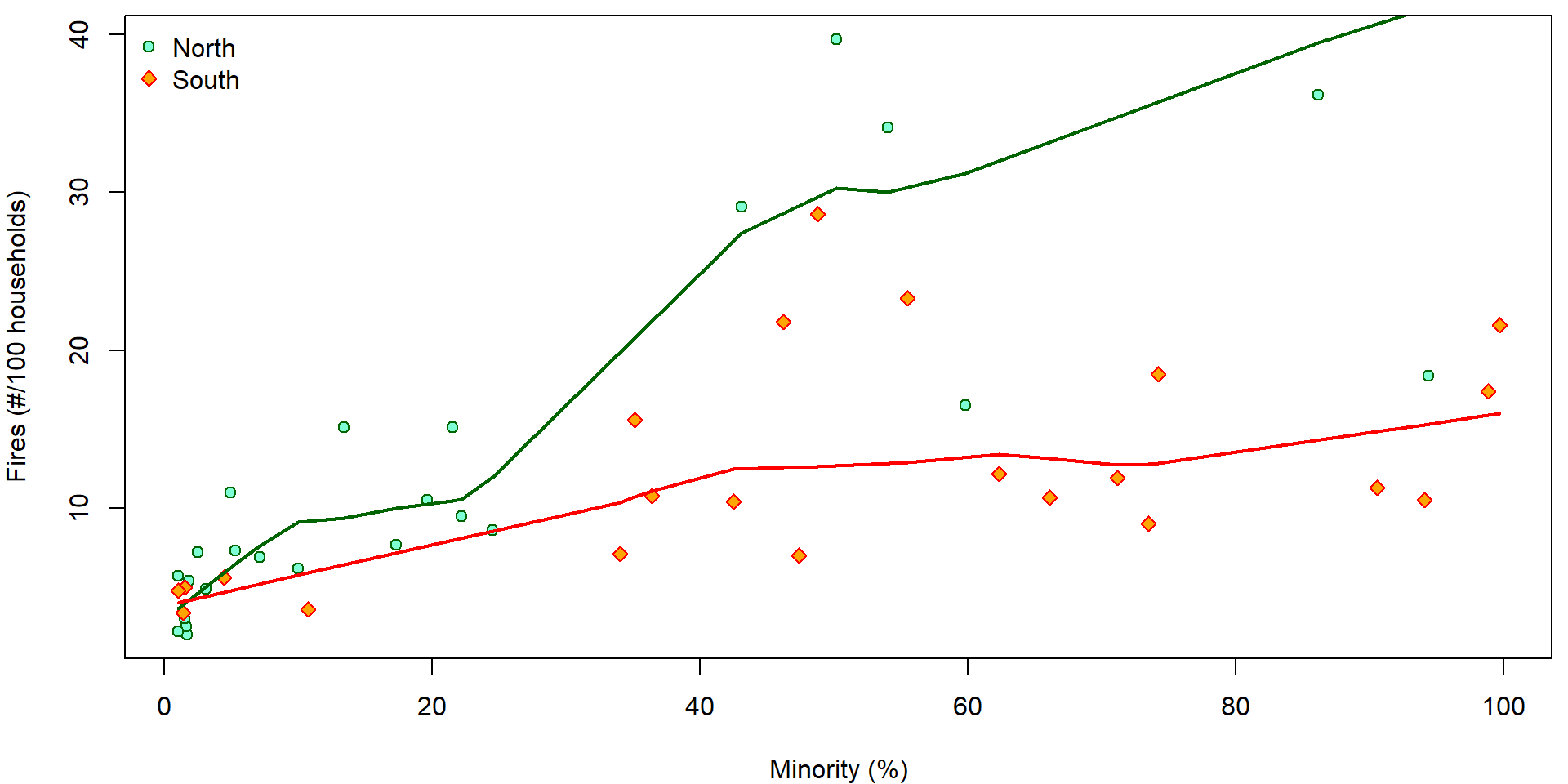
- How would you interpret the plot?
- Do we need interactions in the model?
- Does the side of Chicago modify the relationship between the number of fires and the percentage of minority?
Lets compare the following three models. Based on the output describe the effect of the percentage of minority on the number of fires. Describe also the effect of the side.
m <- list()
m[["Line"]] <- lm(fire ~ minor * fside, data = chicago)
m[["Log2"]] <- lm(fire ~ log2(minor) * fside, data = chicago)
m[["Parab"]] <- lm(fire ~ (minor + I(minor^2)) * fside, data = chicago)
summary(m[["Line"]])##
## Call:
## lm(formula = fire ~ minor * fside, data = chicago)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.26 -3.34 -1.47 3.08 18.30
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.1952 1.6921 3.07 0.0037 **
## minor 0.3227 0.0490 6.59 5e-08 ***
## fsideSouth 1.3745 3.1025 0.44 0.6600
## minor:fsideSouth -0.2081 0.0659 -3.16 0.0029 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.53 on 43 degrees of freedom
## Multiple R-squared: 0.539, Adjusted R-squared: 0.506
## F-statistic: 16.7 on 3 and 43 DF, p-value: 2.38e-07summary(m[["Log2"]])##
## Call:
## lm(formula = fire ~ log2(minor) * fside, data = chicago)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.597 -4.660 -0.875 2.285 17.383
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.173 2.272 -0.08 0.940
## log2(minor) 3.981 0.598 6.65 4.1e-08 ***
## fsideSouth 2.918 4.188 0.70 0.490
## log2(minor):fsideSouth -2.018 0.896 -2.25 0.029 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.44 on 43 degrees of freedom
## Multiple R-squared: 0.552, Adjusted R-squared: 0.521
## F-statistic: 17.6 on 3 and 43 DF, p-value: 1.29e-07summary(m[["Parab"]])##
## Call:
## lm(formula = fire ~ (minor + I(minor^2)) * fside, data = chicago)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.763 -3.918 -0.572 3.096 14.322
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.02190 1.82254 1.11 0.2737
## minor 0.75499 0.14458 5.22 5.5e-06 ***
## I(minor^2) -0.00529 0.00169 -3.14 0.0032 **
## fsideSouth 1.72111 3.41937 0.50 0.6174
## minor:fsideSouth -0.43592 0.19456 -2.24 0.0305 *
## I(minor^2):fsideSouth 0.00317 0.00212 1.50 0.1418
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.86 on 41 degrees of freedom
## Multiple R-squared: 0.647, Adjusted R-squared: 0.604
## F-statistic: 15 on 5 and 41 DF, p-value: 2.23e-08And the corresponding diagnostics:
par(mar = c(4,4,2,0.5))
plotLM(m[["Line"]])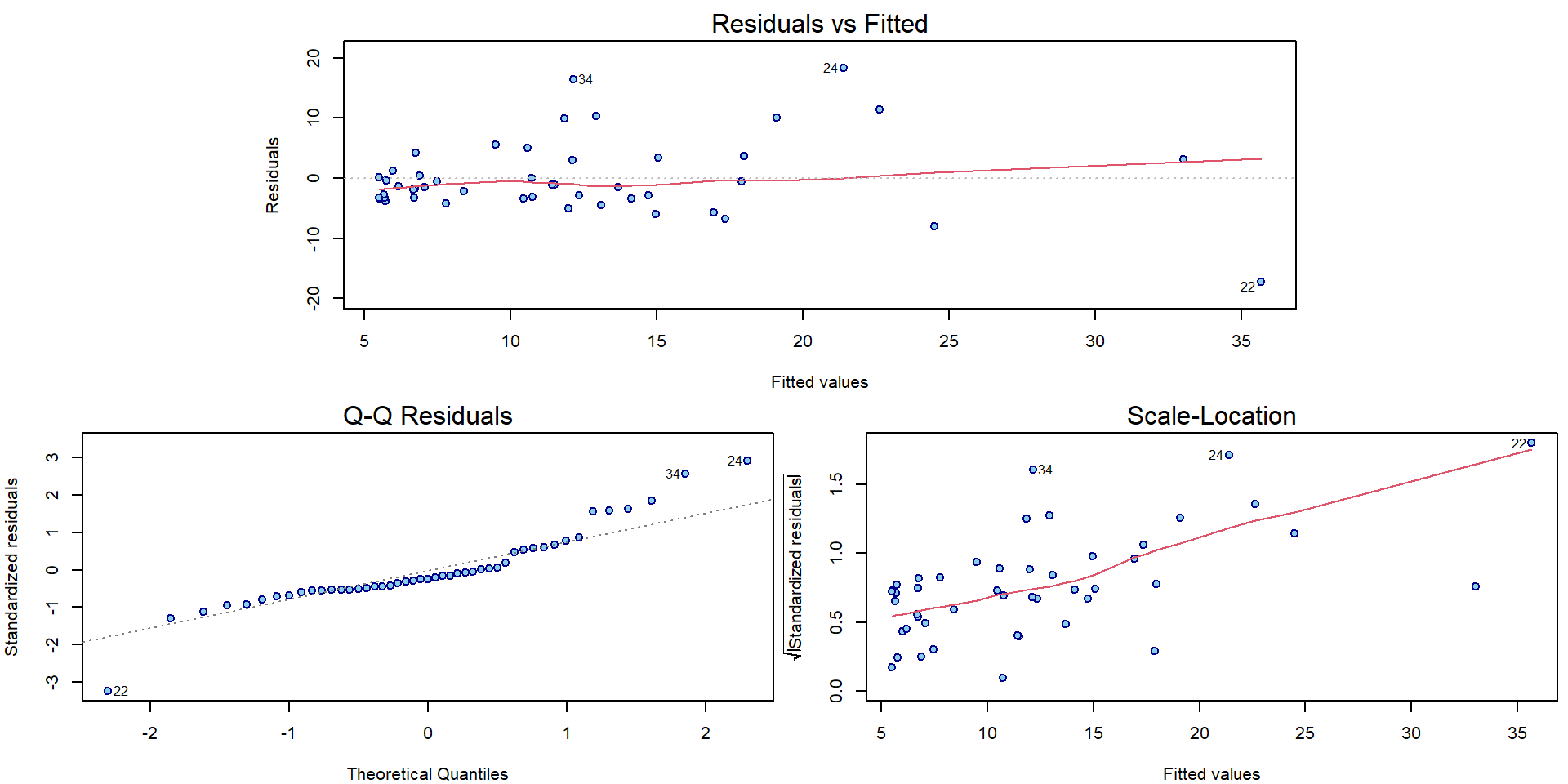
plotLM(m[["Log2"]])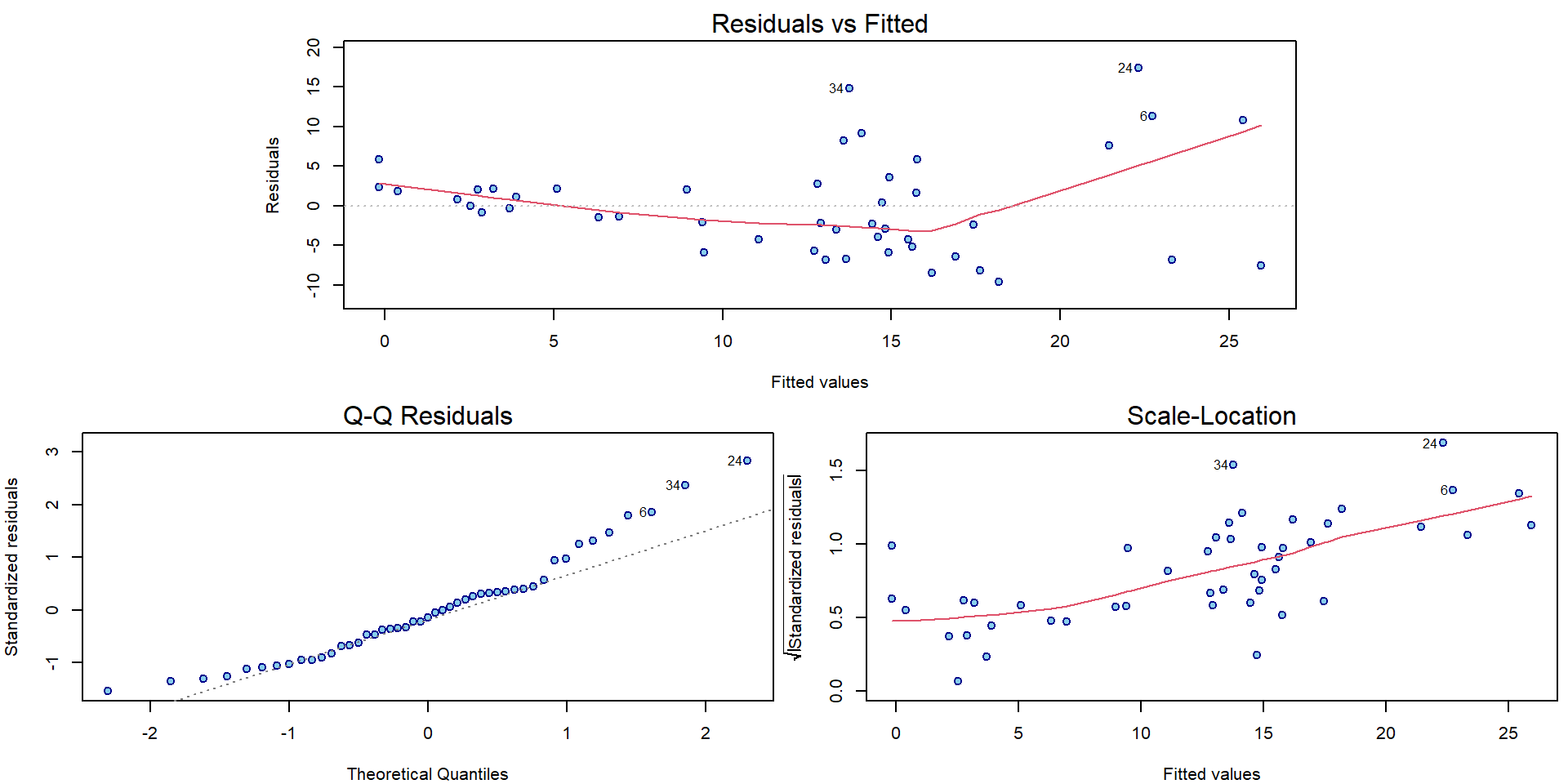
plotLM(m[["Parab"]])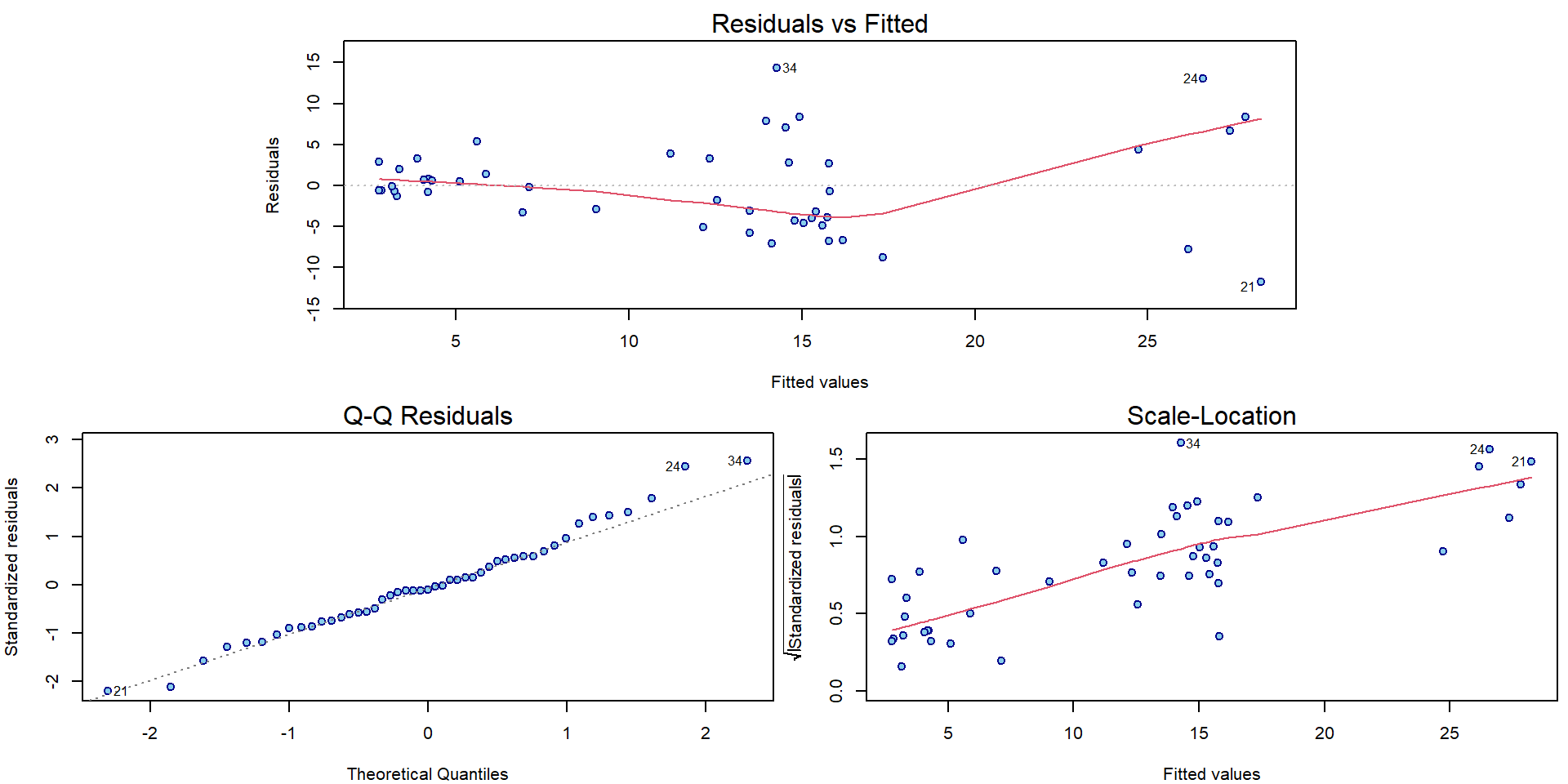
For all three models there can be some issues spotted in the diagnostic plots above (heteroscedasticity, conditional mean specification, maybe normality issues).
Some statistical tests for normality applied to residuals that are heteroscedastic (even in homoscedastic model):
shapiro.test(residuals(m[["Line"]])) ##
## Shapiro-Wilk normality test
##
## data: residuals(m[["Line"]])
## W = 0.9, p-value = 9e-04dagoTest(residuals(m[["Line"]]))##
## Title:
## D'Agostino Normality Test
##
## Test Results:
## STATISTIC:
## Chi2 | Omnibus: 9.4764
## Z3 | Skewness: 2.1817
## Z4 | Kurtosis: 2.1717
## P VALUE:
## Omnibus Test: 0.008754
## Skewness Test: 0.02913
## Kurtosis Test: 0.02987Some statistical tests for normality applied to standardized residuals that are not normal (even in normal linear model):
shapiro.test(stdres(m[["Line"]])) ##
## Shapiro-Wilk normality test
##
## data: stdres(m[["Line"]])
## W = 0.9, p-value = 7e-04dagoTest(stdres(m[["Line"]]))##
## Title:
## D'Agostino Normality Test
##
## Test Results:
## STATISTIC:
## Chi2 | Omnibus: 7.9183
## Z3 | Skewness: 1.3467
## Z4 | Kurtosis: 2.4707
## P VALUE:
## Omnibus Test: 0.01908
## Skewness Test: 0.1781
## Kurtosis Test: 0.01348Statistical test for homoscedasticity (Breusch-Pagan test and Koenker’s studentized version) with alternatives \(\mathsf{var} \left[ Y_i | \mathbf{X}_i\right] = \sigma^2 \exp\left\{\tau \mathsf{E} \left[Y_i | \mathbf{X}_i\right]\right\}\) or in general \(\mathsf{var} \left[ Y_i | \mathbf{X}_i, \mathbf{Z_i}\right] = \sigma^2 \exp\left\{\mathbf{Z}_i^\top \boldsymbol{\tau}\right\}\):
ncvTest(m[["Line"]]) # default is fitted## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 25.24, Df = 1, p = 5.1e-07ncvTest(m[["Line"]], var.formula = ~fitted(m[["Line"]])) # the same as before ## Non-constant Variance Score Test
## Variance formula: ~ fitted(m[["Line"]])
## Chisquare = 25.24, Df = 1, p = 5.1e-07bptest(m[["Line"]], varformula = ~fitted(m[["Line"]])) # Koenker's studentized version (robust to non-normality)##
## studentized Breusch-Pagan test
##
## data: m[["Line"]]
## BP = 14, df = 1, p-value = 2e-04bptest(m[["Line"]]) # default is the same as model formula##
## studentized Breusch-Pagan test
##
## data: m[["Line"]]
## BP = 15, df = 3, p-value = 0.002In addition, there is also a bunch of points scattered around the origin and relatively only a few observations are given for larger proportion of the minority or the larger amount of fires. This suggests that log transformation (of the response and the predictor as well) could help.
2. Response (logarithmic) transformation
Typically, when the residual variance increases with the response expectation, log-transformation of the response often ensures a homoscedastic model (Assumption A3a from the lecture).
Firstly, compare the plot below (on the log scale on \(y\) axes) with the previous plot on the original scale on the \(y\) axes:
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
LYLAB <- "Log(Fires)"
plot(log(fire) ~ minor, data = chicago,
xlab = XLAB, ylab = LYLAB,
col = COLS[fside], bg = BGS[fside], pch = PCHS[fside])
legend("topleft", legend = c("North", "South"), bty = "n",
pch = PCHS, col = COLS, pt.bg = BGS)
lines(with(subset(chicago, fside == "North"), lowess(minor, log(fire))),
col = COLS["North"], lwd = 2)
lines(with(subset(chicago, fside == "South"), lowess(minor, log(fire))),
col = COLS["South"], lwd = 2)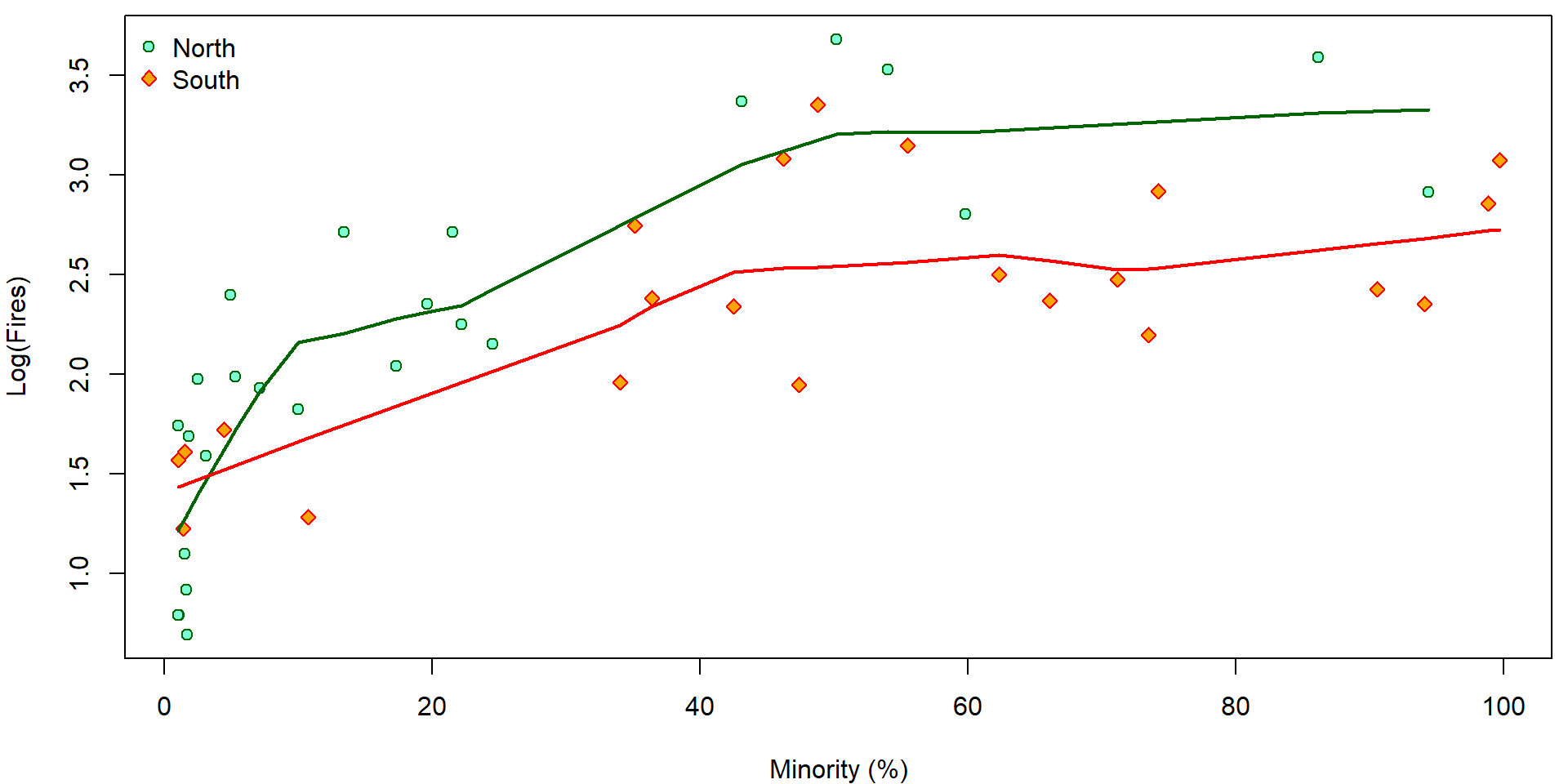
Using the proposed transformation of the response we also change the underlying data. This means, that instead of the model \[ \mathsf{E} [Y_i | \boldsymbol{X}_i] = \boldsymbol{X}_i^\top \boldsymbol{\beta} \] fitted based on the random sample \(\{(Y_i, \boldsymbol{X}_i);\; i = 1, \dots, n\}\) we fit another model of the form \[ \mathsf{E} [\log(Y_i) | \boldsymbol{X}_i] = \boldsymbol{X}_i^\top \widetilde{\boldsymbol{\beta}} \] which is, however, based on the different random sample \(\{(\log(Y_i), \boldsymbol{X}_i);\;i = 1, \dots, n\}\). This also has some crucial consequences. The logarithmic transformation will help to deal with some issues regarding heteroscedastic data but, on the other hand, it will introduce new problems regarding the model interpretability.
The idea is that the final model should be (always) interpreted with
respect to the original data - the information about
the number of fires (fire) - not the logarithm of the
number of fires (log(fire)).
For some better interpretation we will also use the log
transformation of the independent variable – the information about the
proportion of minority – minor. What is the interpretation
of the following model:
summary(m <- lm(log(fire) ~ log2(minor) * fside, data = chicago))##
## Call:
## lm(formula = log(fire) ~ log2(minor) * fside, data = chicago)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.752 -0.340 -0.079 0.346 0.849
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.0162 0.1463 6.94 1.6e-08 ***
## log2(minor) 0.3596 0.0385 9.33 6.7e-12 ***
## fsideSouth 0.2796 0.2698 1.04 0.306
## log2(minor):fsideSouth -0.1441 0.0577 -2.50 0.016 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.415 on 43 degrees of freedom
## Multiple R-squared: 0.728, Adjusted R-squared: 0.709
## F-statistic: 38.3 on 3 and 43 DF, p-value: 3.23e-12The diagnostic plots have improved in terms of mean and variance:
par(mar = c(4,4,2,0.5))
plotLM(m)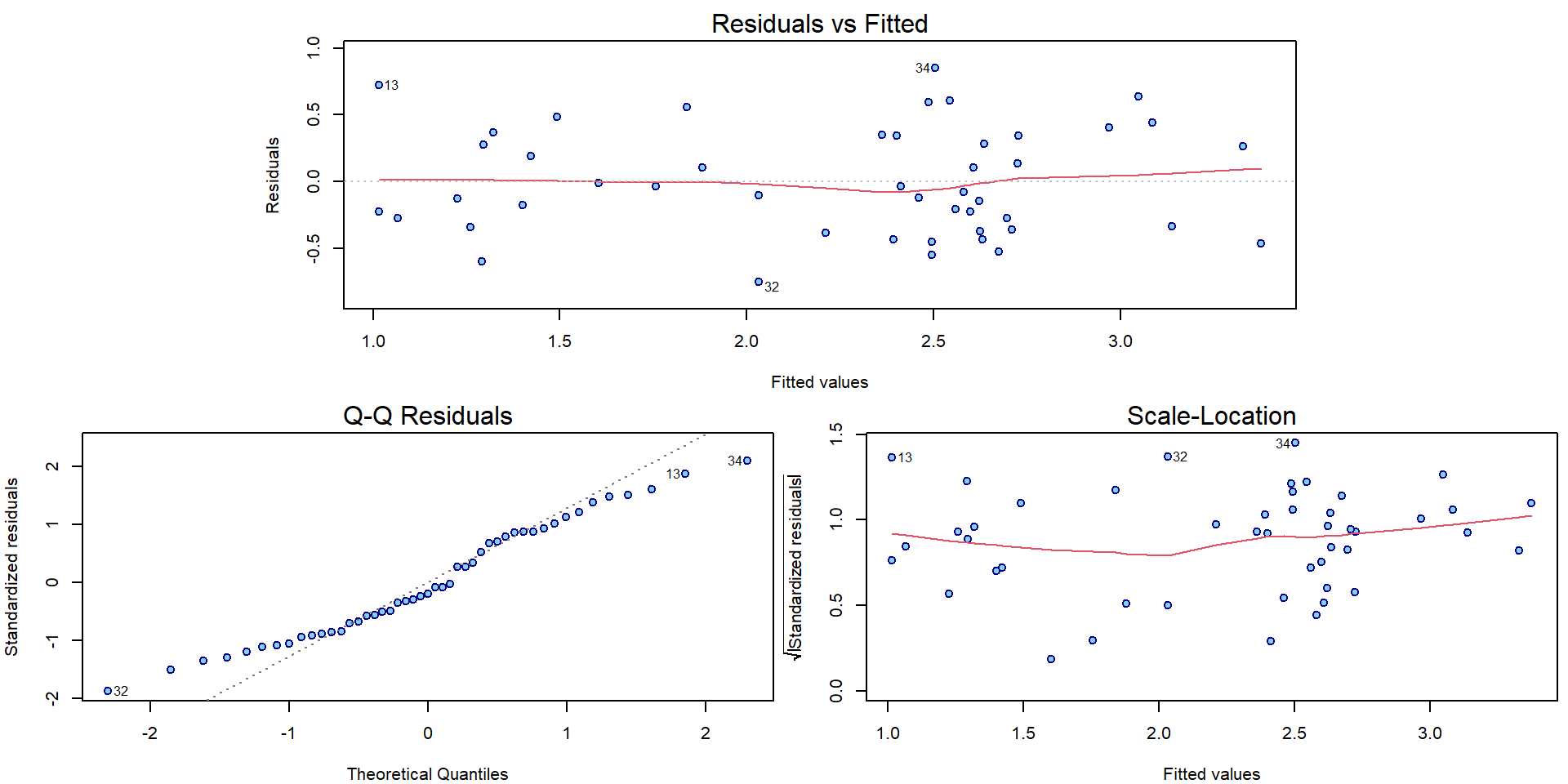
Recall the Jensen inequality and the fact that \[ \mathsf{E} [\log(Y_i) | \boldsymbol{X}_i] \neq \log(\mathsf{E} [Y_i | \boldsymbol{X}_i]) \qquad \text{but rather} \qquad \mathsf{E} [\log(Y_i) | \boldsymbol{X}_i] < \log(\mathsf{E} [Y_i | \boldsymbol{X}_i]). \] And now compare the two models: \[ \begin{aligned} Y_i &= \mathbf{X}_i^\top \boldsymbol{\beta} + \varepsilon_i, \\ \log Y_i = \mathbf{X}_i^\top \widetilde{\boldsymbol{\beta}} + \widetilde{\varepsilon}_i \quad\Longleftrightarrow\quad Y_i &= \exp\left\{\mathbf{X}_i^\top \widetilde{\boldsymbol{\beta}}\right\} \cdot \exp\left\{ \widetilde{\varepsilon}_i \right\}. \end{aligned} \]
What are the consequences with respect to the interpretation of the parameter estimates provided in the summary output above? What would be a suitable interpretation that we can use in this situation?
\[ \dfrac{ \mathsf{E} \left[Y_i | \mathbf{X}_i = \mathbf{x} + \mathbf{e}_j\right] }{ \mathsf{E} \left[Y_i | \mathbf{X}_i = \mathbf{x}\right] } = \dfrac{ \exp \left\{ (\mathbf{x} + \mathbf{e}_j)^\top \widetilde{\boldsymbol{\beta}} \right\} \mathsf{E} \exp\left\{ \widetilde{\varepsilon}_i \right\} }{ \exp \left\{ \mathbf{x}^\top \widetilde{\boldsymbol{\beta}} \right\} \mathsf{E} \exp\left\{ \widetilde{\varepsilon}_i \right\} } = \exp \widetilde{\beta}_j \]
It is easy to visualize the fitted regression function. In addition, we can also add the confidence bands AROUND the regression function and the prediction bands. However, given the previous problems related to the Jensen inequality, only the prediction bands make sense for this model and the confidence (AROUND) bands do not have any good interpretation here.
lpred <- 500
pminor <- seq(1, 100, length = lpred)
pdata <- data.frame(minor = rep(pminor, 2),
fside = factor(rep(c("North", "South"),
each = lpred)))
cifit <- predict(m, newdata = pdata, interval = "confidence", se.fit = TRUE)
pfit <- predict(m, newdata = pdata, interval = "prediction")
YLIM <- range(log(chicago[, "fire"]), pfit)
XLIM <- range(chicago[, "minor"])
par(mfrow = c(1, 2), mar=c(4,4,2,0.5))
for (ss in levels(chicago[, "fside"])){
plot(log(fire) ~ minor, data = subset(chicago, fside == ss), main = ss,
xlab = XLAB, ylab = LYLAB, xlim = XLIM, ylim = YLIM,
col = COLS[fside], bg = BGS[fside], pch = PCHS[fside])
ind <- if (ss == "North") 1:lpred else (lpred + 1):(2 * lpred)
lines(pminor, cifit$fit[ind, "fit"], col = COLS[ss], lwd = 3)
lines(pminor, cifit$fit[ind, "lwr"], col = COLS[ss], lwd = 2, lty = 2)
lines(pminor, cifit$fit[ind, "upr"], col = COLS[ss], lwd = 2, lty = 2)
lines(pminor, pfit[ind, "lwr"], col = COLS[ss], lwd = 2, lty = 3)
lines(pminor, pfit[ind, "upr"], col = COLS[ss], lwd = 2, lty = 3)
legend(x=25, y=1, bty = "n",
legend=c("estim. E[log(Y)|X=x]",
"conf. band around E[log(Y)|X=x]",
"prediction band for log(Y)"),
lwd=c(3,2,2), lty=c(1,2,3), col=COLS[ss])
} 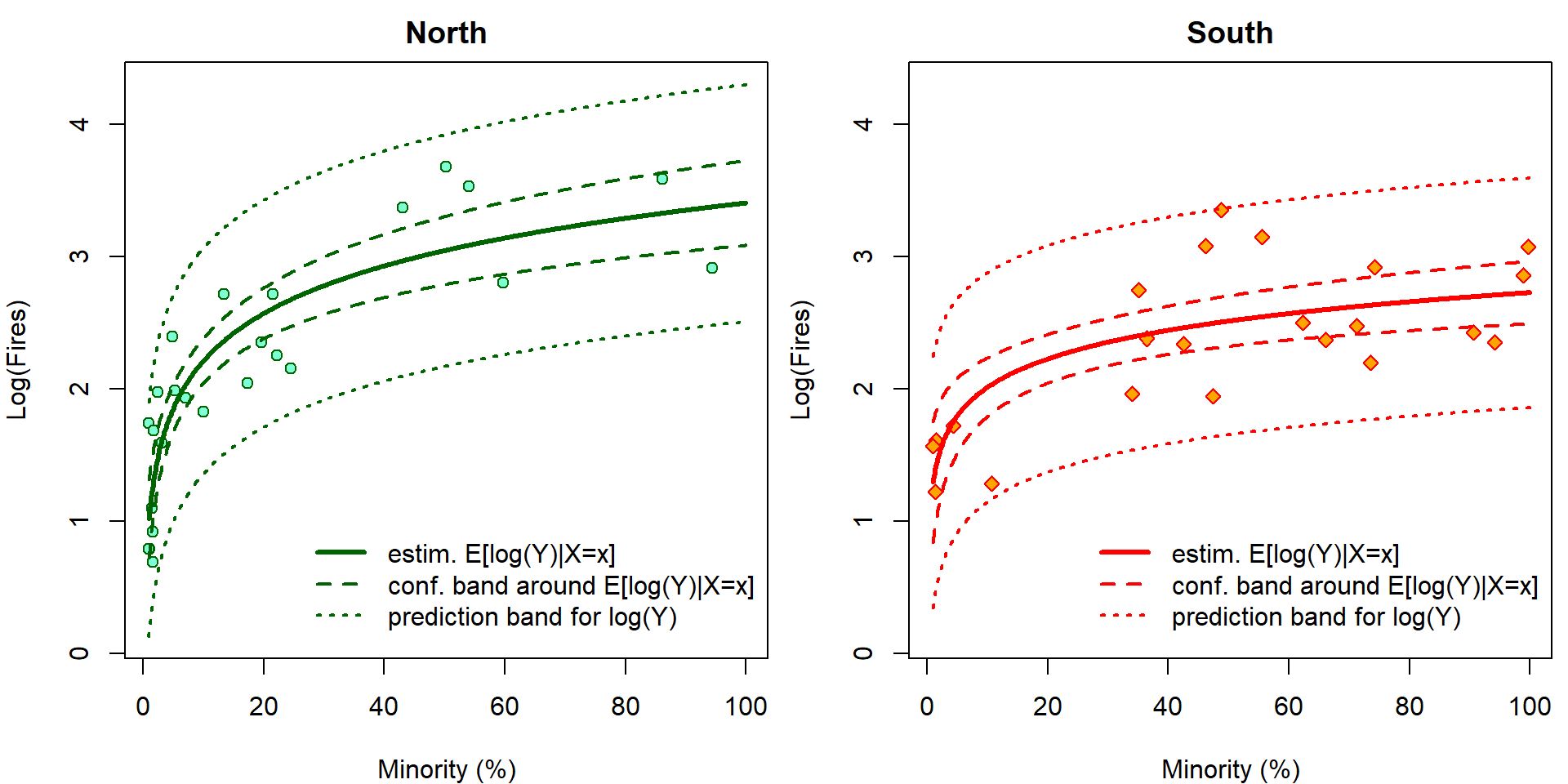
The confidence intervals \[ \mathsf{P} \left( (LCI, UCI)\ni \mathbf{x}^\top \widetilde{\boldsymbol{\beta}} = \mathsf{E}\left[\log Y | \mathbf{X}= \mathbf{x} \right] \right) \] cannot be interpreted with respect to original scale by simple \(\exp\) transformation \[ \mathsf{P} \left( (\exp\{LCI\}, \exp\{UCI\})\ni \exp\{\mathbf{x}^\top \widetilde{\boldsymbol{\beta}}\} = \exp\left\{\mathsf{E}\left[\log Y | \mathbf{X}= \mathbf{x} \right]\right\} < \mathsf{E}\left[Y | \mathbf{X}= \mathbf{x} \right] \right). \] However, it still works for prediction intervals: \[ \mathsf{P} \left( \log Y_{new} \in (LPI, UPI) \right) = \mathsf{P} \left( Y_{new} \in (\exp\{LPI\}, \exp\{UPI\}) \right). \] Now we plot the same outputs but on original scales. Grey colors correspond to incorrect estimates for \(\exp {\mathsf{E} [\log Y | \mathbf{X} ]}\) that are simple \(\exp\) transformation of the estimates for \(\mathsf{E} [\log Y | \mathbf{X} ]\). Using \(\Delta\)-method and knowledge of log-normal distribution, \(\mathsf{E} \exp{ \varepsilon} = \exp \left\{\frac{\sigma^2}{2}\right\}\), we can calculate the true estimates for \(\mathsf{E} \left[ Y | \mathbf{X}\right]\) (colourful).
YLIM <- range(chicago[, "fire"], exp(pfit))
XLIM <- range(chicago[, "minor"])
# True point estimate and CI for E[Y|X] based on log-N distribution
sigma2 <- summary(m)$sigma^2
EYX_fit <- exp(cifit$fit[,"fit"] + sigma2/2)
CIEYX_lwr <- EYX_fit * (1 - qnorm(0.975) * cifit$se.fit)
CIEYX_upr <- EYX_fit * (1 + qnorm(0.975) * cifit$se.fit)
par(mfrow = c(1, 2), mar=c(4,4,2,0.5))
for (ss in levels(chicago[, "fside"])){
plot(fire ~ minor, data = subset(chicago, fside == ss), main = ss,
xlab = XLAB, ylab = "Fires", xlim = XLIM, ylim = YLIM,
col = COLS[fside], bg = BGS[fside], pch = PCHS[fside])
ind <- if (ss == "North") 1:lpred else (lpred + 1):(2 * lpred)
lines(pminor, exp(cifit$fit[ind, "fit"]), col = "grey30", lwd = 3)
lines(pminor, exp(cifit$fit[ind, "lwr"]), col = "grey40", lwd = 2, lty = 2)
lines(pminor, exp(cifit$fit[ind, "upr"]), col = "grey40", lwd = 2, lty = 2)
lines(pminor, EYX_fit[ind], col = COLS[ss], lwd = 3)
lines(pminor, CIEYX_lwr[ind], col = COLS[ss], lwd = 2, lty = 2)
lines(pminor, CIEYX_upr[ind], col = COLS[ss], lwd = 2, lty = 2)
lines(pminor, exp(pfit[ind, "lwr"]), col = COLS[ss], lwd = 2, lty = 3)
lines(pminor, exp(pfit[ind, "upr"]), col = COLS[ss], lwd = 2, lty = 3)
legend("topleft", bty = "n",
legend=c("estim. exp(E[log(Y)|X=x]) < E[Y|X=x]",
"conf. band around exp(E[log(Y)|X=x]) < E[Y|X=x]",
"estim. E[Y|X=x]",
"conf. band around E[Y|X=x]",
"prediction band for Y"),
lwd=c(3,2,3,2,2), lty=c(1,2,1,2,3),
col=c("grey30","grey40",COLS[ss],COLS[ss],COLS[ss]))
} 
3. Regression planes
Now, we will try to improve the model by adding the information about
insurance policies (the independent variable insur). We
will fit the following model:
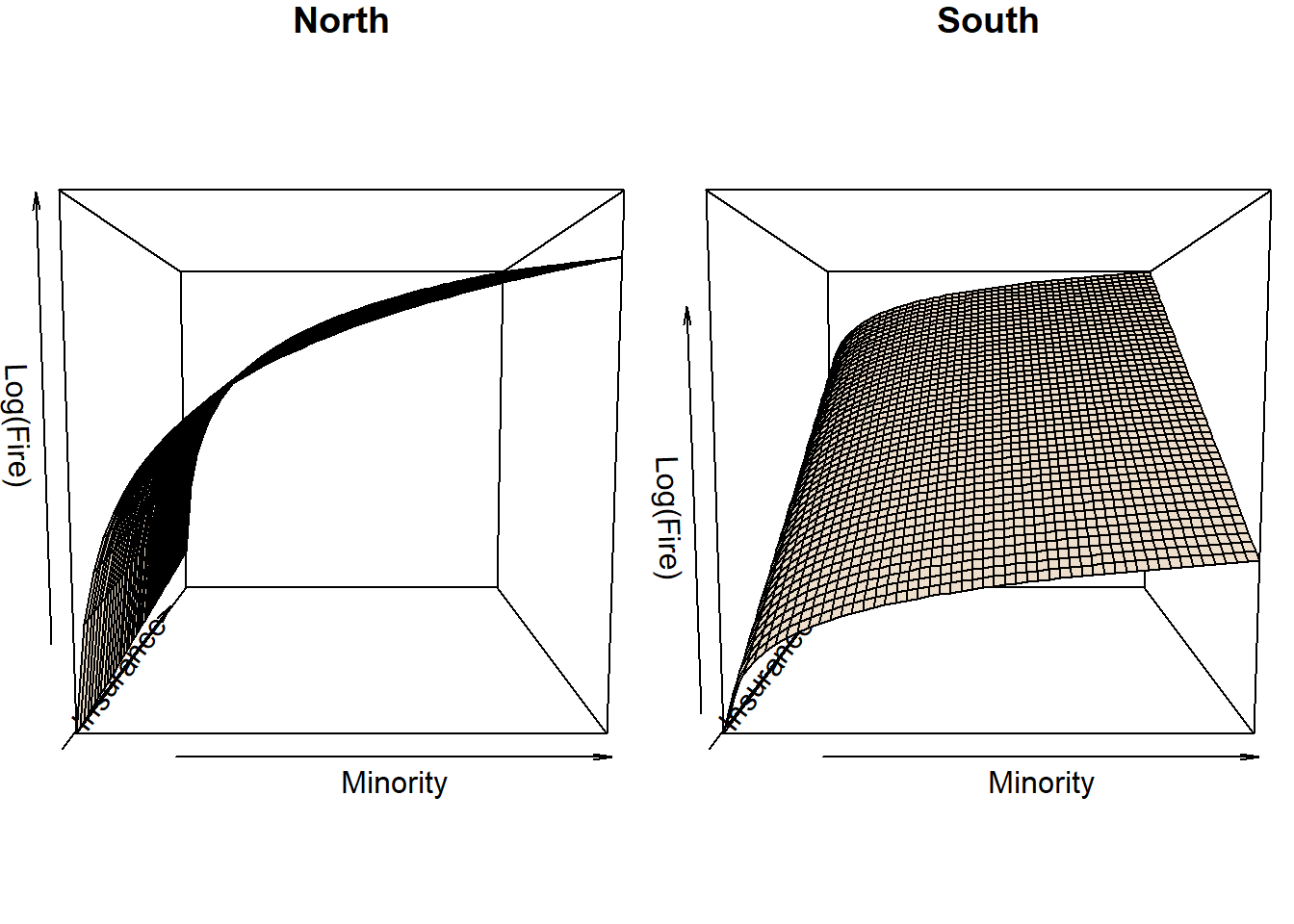
m2 <- lm(log(fire) ~ (log(minor) + insur) * fside, data = chicago)Note, that the fitted regression planes describing the dependence of
log(fire) on log(minor) and insur
based on the m2 model are the same as if the model is
fitted separately in the North and South side of Chicago.
Hence, if we are interested in just a description of those planes -
the conditional mean structure (and are lazy to extract the appropriate
intercepts and slopes from the m2 model), we can fit
separate North/South models and take the coefficients from there.
Compare the output above with the following two models:
m2North <- lm(log(fire) ~ log(minor) + insur, data = chicago,
subset = (fside == "North"))
m2South <- lm(log(fire) ~ log(minor) + insur, data = chicago,
subset = (fside == "South")) Individual work
Consider the model above and try to answer the following questions:
- Can you reconstruct the (mean) parameter estimates from the
m2model above using the two separate models for the north and south sides of Chicago? Can you do it vice versa? - Try some different parametrization of the locality. For instance
summary(lm(log(fire) ~ (log(minor) + insur) * fside, data = chicago,
contrasts = list(fside = contr.sum)))##
## Call:
## lm(formula = log(fire) ~ (log(minor) + insur) * fside, data = chicago,
## contrasts = list(fside = contr.sum))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.6025 -0.2690 -0.0683 0.2337 0.6975
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.2181 0.1211 10.06 1.2e-12 ***
## log(minor) 0.3109 0.0527 5.90 5.9e-07 ***
## insur 0.3732 0.1253 2.98 0.0048 **
## fside1 -0.1751 0.1211 -1.45 0.1556
## log(minor):fside1 0.1652 0.0527 3.14 0.0032 **
## insur:fside1 -0.2419 0.1253 -1.93 0.0604 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.365 on 41 degrees of freedom
## Multiple R-squared: 0.799, Adjusted R-squared: 0.774
## F-statistic: 32.5 on 5 and 41 DF, p-value: 2.96e-13contr.sum(2)## [,1]
## 1 1
## 2 -1What is the interpretation of the estimated parameters in the summary output above?
Plotting the planes:
K <- 50
phi <- 5
minorGrid <- seq(1, 100, length = K)
insurGrid <- seq(0, 2.2, length = K)
xyGrid <- expand.grid(minorGrid, insurGrid)
par(mfrow = c(1, 2), mar = c(1,1,1,0))
newdata <- pred <- conf <- lfire <- list()
for(loc in c("North", "South")){
newdata[[loc]] <- data.frame(minor = rep(minorGrid, K),
insur = rep(insurGrid, each = K),
fside = loc)
conf[[loc]] <- predict(m2, newdata = newdata[[loc]], interval = "confidence")
pred[[loc]] <- predict(m2, newdata = newdata[[loc]], interval = "predict")
lfire[[loc]] <- matrix(conf[[loc]][,"fit"], nrow = K, ncol = K)
persp(minorGrid, insurGrid, lfire[[loc]],
xlab = "Minority", ylab = "Insurance", zlab = "Log(Fire)",
phi = phi, col = "antiquewhite2", main=loc)
}
An interactive plot:
library(rgl)
persp3d(minorGrid, insurGrid, lfire[["North"]],
xlab = "Minority", ylab = "Insurance", zlab = "Log(Fire)", col = "seagreen")
persp3d(minorGrid, insurGrid, matrix(pred[["North"]][,"upr"], nrow = K, ncol = K),
col = "aquamarine", add=T)
persp3d(minorGrid, insurGrid, matrix(pred[["North"]][,"lwr"], nrow = K, ncol = K),
col = "aquamarine", add=T)
persp3d(minorGrid, insurGrid, lfire[["South"]], col = "orange", add=T)
persp3d(minorGrid, insurGrid, matrix(pred[["South"]][,"upr"], nrow = K, ncol = K),
col = "gold", add=T)
persp3d(minorGrid, insurGrid, matrix(pred[["South"]][,"lwr"], nrow = K, ncol = K),
col = "gold", add=T)
with(subset(chicago, fside == "North"),
plot3d(minor, insur, log(fire), add = TRUE, size = 7, col = "darkgreen"))
with(subset(chicago, fside == "South"),
plot3d(minor, insur, log(fire), add = TRUE, size = 7, col = "red"))