Review of statistical methods
Jan Vávra
Exercise 1
Download this R markdown as: R, Rmd.
Loading the data and libraries
If you use your personal computer an additional package
mffSM is needed. The package is not available from CRAN but
can be downloaded from this website. Download the package and use the following
command for the installation:
install.packages("mffSM_1.1.zip", repos = NULL)
# or without necessity to download first
install.packages("https://www2.karlin.mff.cuni.cz/~komarek/vyuka/2021_22/nmsa407/R/mffSM_1.2.tar.gz", repos = NULL)Libraries can be accessed the following way. When in doubt, use
help() or ? to show the documentation:
library("mffSM")
library("colorspace")
help(package="mffSM")This lab session we will work with the data set on car vehicles that were on the market in the U.S. in 2004:
data(Cars2004nh, package = "mffSM")Quick overview and summary of the data:
dim(Cars2004nh)## [1] 425 20str(Cars2004nh)## 'data.frame': 425 obs. of 20 variables:
## $ vname : chr "Chevrolet.Aveo.4dr" "Chevrolet.Aveo.LS.4dr.hatch" "Chevrolet.Cavalier.2dr" "Chevrolet.Cavalier.4dr" ...
## $ type : int 1 1 1 1 1 1 1 1 1 1 ...
## $ drive : int 1 1 1 1 1 1 1 1 1 1 ...
## $ price.retail: int 11690 12585 14610 14810 16385 13670 15040 13270 13730 15460 ...
## $ price.dealer: int 10965 11802 13697 13884 15357 12849 14086 12482 12906 14496 ...
## $ price : num 11328 12194 14154 14347 15871 ...
## $ cons.city : num 8.4 8.4 9 9 9 8.1 8.1 9 8.7 9 ...
## $ cons.highway: num 6.9 6.9 6.4 6.4 6.4 6.5 6.5 7.1 6.5 7.1 ...
## $ consumption : num 7.65 7.65 7.7 7.7 7.7 7.3 7.3 8.05 7.6 8.05 ...
## $ engine.size : num 1.6 1.6 2.2 2.2 2.2 2 2 2 2 2 ...
## $ ncylinder : int 4 4 4 4 4 4 4 4 4 4 ...
## $ horsepower : int 103 103 140 140 140 132 132 130 110 130 ...
## $ weight : int 1075 1065 1187 1214 1187 1171 1191 1185 1182 1182 ...
## $ iweight : num 0.00093 0.000939 0.000842 0.000824 0.000842 ...
## $ lweight : num 6.98 6.97 7.08 7.1 7.08 ...
## $ wheel.base : int 249 249 264 264 264 267 267 262 262 262 ...
## $ length : int 424 389 465 465 465 442 442 427 427 427 ...
## $ width : int 168 168 175 173 175 170 170 170 170 170 ...
## $ ftype : Factor w/ 6 levels "personal","wagon",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ fdrive : Factor w/ 3 levels "front","rear",..: 1 1 1 1 1 1 1 1 1 1 ...head(Cars2004nh)## vname type drive price.retail price.dealer price cons.city cons.highway consumption
## 1 Chevrolet.Aveo.4dr 1 1 11690 10965 11328 8.4 6.9 7.65
## 2 Chevrolet.Aveo.LS.4dr.hatch 1 1 12585 11802 12194 8.4 6.9 7.65
## 3 Chevrolet.Cavalier.2dr 1 1 14610 13697 14154 9.0 6.4 7.70
## 4 Chevrolet.Cavalier.4dr 1 1 14810 13884 14347 9.0 6.4 7.70
## 5 Chevrolet.Cavalier.LS.2dr 1 1 16385 15357 15871 9.0 6.4 7.70
## 6 Dodge.Neon.SE.4dr 1 1 13670 12849 13260 8.1 6.5 7.30
## engine.size ncylinder horsepower weight iweight lweight wheel.base length width ftype fdrive
## 1 1.6 4 103 1075 0.0009302 6.980 249 424 168 personal front
## 2 1.6 4 103 1065 0.0009390 6.971 249 389 168 personal front
## 3 2.2 4 140 1187 0.0008425 7.079 264 465 175 personal front
## 4 2.2 4 140 1214 0.0008237 7.102 264 465 173 personal front
## 5 2.2 4 140 1187 0.0008425 7.079 264 465 175 personal front
## 6 2.0 4 132 1171 0.0008540 7.066 267 442 170 personal frontsummary(Cars2004nh)## vname type drive price.retail price.dealer price
## Length:425 Min. :1.00 Min. :1.00 Min. : 10280 Min. : 9875 Min. : 10078
## Class :character 1st Qu.:1.00 1st Qu.:1.00 1st Qu.: 20370 1st Qu.: 18973 1st Qu.: 19600
## Mode :character Median :1.00 Median :1.00 Median : 27905 Median : 25672 Median : 26656
## Mean :2.22 Mean :1.69 Mean : 32866 Mean : 30096 Mean : 31481
## 3rd Qu.:3.00 3rd Qu.:2.00 3rd Qu.: 39235 3rd Qu.: 35777 3rd Qu.: 37514
## Max. :6.00 Max. :3.00 Max. :192465 Max. :173560 Max. :183012
##
## cons.city cons.highway consumption engine.size ncylinder horsepower weight
## Min. : 6.2 Min. : 5.10 Min. : 5.65 Min. :1.30 Min. :-1.00 Min. :100 Min. : 923
## 1st Qu.:11.2 1st Qu.: 8.10 1st Qu.: 9.65 1st Qu.:2.40 1st Qu.: 4.00 1st Qu.:165 1st Qu.:1412
## Median :12.4 Median : 9.00 Median :10.70 Median :3.00 Median : 6.00 Median :210 Median :1577
## Mean :12.4 Mean : 9.14 Mean :10.75 Mean :3.21 Mean : 5.79 Mean :217 Mean :1626
## 3rd Qu.:13.8 3rd Qu.: 9.80 3rd Qu.:11.65 3rd Qu.:3.90 3rd Qu.: 6.00 3rd Qu.:255 3rd Qu.:1804
## Max. :23.5 Max. :19.60 Max. :21.55 Max. :8.30 Max. :12.00 Max. :500 Max. :3261
## NA's :14 NA's :14 NA's :14 NA's :2
## iweight lweight wheel.base length width ftype fdrive
## Min. :0.0003 Min. :6.83 Min. :226 Min. :363 Min. :163 personal:242 front:223
## 1st Qu.:0.0006 1st Qu.:7.25 1st Qu.:262 1st Qu.:450 1st Qu.:175 wagon : 30 rear :110
## Median :0.0006 Median :7.36 Median :272 Median :472 Median :180 SUV : 60 4x4 : 92
## Mean :0.0006 Mean :7.37 Mean :275 Mean :471 Mean :181 pickup : 24
## 3rd Qu.:0.0007 3rd Qu.:7.50 3rd Qu.:284 3rd Qu.:490 3rd Qu.:185 sport : 49
## Max. :0.0011 Max. :8.09 Max. :366 Max. :577 Max. :206 minivan : 20
## NA's :2 NA's :2 NA's :2 NA's :26 NA's :28Data subsampling and preprocessing
Exclude cars where the consumption is missing:
Cars2004nh <- Cars2004nh[!is.na(Cars2004nh$consumption),] Create a working subsample:
set.seed(20250218)
idx <- c(sample((1:nrow(Cars2004nh))[Cars2004nh$ftype=="personal"], size=100),
sample((1:nrow(Cars2004nh))[Cars2004nh$ftype!="personal"], size=120))
Cars2004nh <- Cars2004nh[idx,]Next, we derive some additional variables. First, binary factor
fdrive2, which distinguishes whether the drive is
front or other (rear or
4x4):
Cars2004nh <- transform(Cars2004nh,
fdrive2 = factor(1*(fdrive == "front") +
2*(fdrive != "front"),
labels = c("front", "other")))
with(Cars2004nh, table(fdrive, fdrive2))## fdrive2
## fdrive front other
## front 106 0
## rear 0 64
## 4x4 0 50Next, we derive binary indicator cons10 of having a
consumption <= 10 l/100 km and then create a factor with
No (0) and Yes (1) labels:
Cars2004nh <- transform(Cars2004nh,
cons10 = 1 * (consumption <= 10), # 0 or 1
fcons10 = factor(1 * (consumption <= 10),
labels = c("No", "Yes")))
summary(Cars2004nh)## vname type drive price.retail price.dealer price
## Length:220 Min. :1.00 Min. :1.00 Min. : 10280 Min. : 9875 Min. : 10078
## Class :character 1st Qu.:1.00 1st Qu.:1.00 1st Qu.: 20334 1st Qu.: 18839 1st Qu.: 19572
## Mode :character Median :2.00 Median :2.00 Median : 27270 Median : 25142 Median : 26147
## Mean :2.62 Mean :1.75 Mean : 32819 Mean : 30012 Mean : 31416
## 3rd Qu.:4.00 3rd Qu.:2.00 3rd Qu.: 40151 3rd Qu.: 35904 3rd Qu.: 38015
## Max. :6.00 Max. :3.00 Max. :126670 Max. :117854 Max. :122262
##
## cons.city cons.highway consumption engine.size ncylinder horsepower weight
## Min. : 6.7 Min. : 5.50 Min. : 6.10 Min. :1.30 Min. :-1.00 Min. :103 Min. : 923
## 1st Qu.:11.2 1st Qu.: 8.10 1st Qu.: 9.65 1st Qu.:2.40 1st Qu.: 4.00 1st Qu.:165 1st Qu.:1384
## Median :12.4 Median : 9.00 Median :10.70 Median :3.20 Median : 6.00 Median :210 Median :1584
## Mean :12.5 Mean : 9.28 Mean :10.88 Mean :3.21 Mean : 5.76 Mean :215 Mean :1625
## 3rd Qu.:13.8 3rd Qu.: 9.80 3rd Qu.:11.80 3rd Qu.:3.90 3rd Qu.: 6.00 3rd Qu.:250 3rd Qu.:1810
## Max. :19.6 Max. :16.80 Max. :17.45 Max. :6.00 Max. :12.00 Max. :493 Max. :2782
##
## iweight lweight wheel.base length width ftype fdrive
## Min. :0.000360 Min. :6.83 Min. :226 Min. :363 Min. :165 personal:100 front:106
## 1st Qu.:0.000552 1st Qu.:7.23 1st Qu.:259 1st Qu.:444 1st Qu.:175 wagon : 17 rear : 64
## Median :0.000631 Median :7.37 Median :272 Median :466 Median :180 SUV : 36 4x4 : 50
## Mean :0.000643 Mean :7.37 Mean :274 Mean :467 Mean :181 pickup : 16
## 3rd Qu.:0.000722 3rd Qu.:7.50 3rd Qu.:287 3rd Qu.:493 3rd Qu.:185 sport : 36
## Max. :0.001083 Max. :7.93 Max. :366 Max. :556 Max. :203 minivan : 15
## NA's :16 NA's :18
## fdrive2 cons10 fcons10
## front:106 Min. :0.00 No :143
## other:114 1st Qu.:0.00 Yes: 77
## Median :0.00
## Mean :0.35
## 3rd Qu.:1.00
## Max. :1.00
## Two sample problem
In this section, we review the methods for two-sample problems, i.e. exploring the relationship between continuous variable and binary variable. In particular, we are going to explore the following question:
Does the consumption depend on the drive while distinguishing only two categories: front and other?
Exploration
We start with an exploration phase. The most straightforward
visualization tool for this problem is boxplot, the default
plot for numeric ~ factor:
plot(consumption ~ fdrive2, data = Cars2004nh)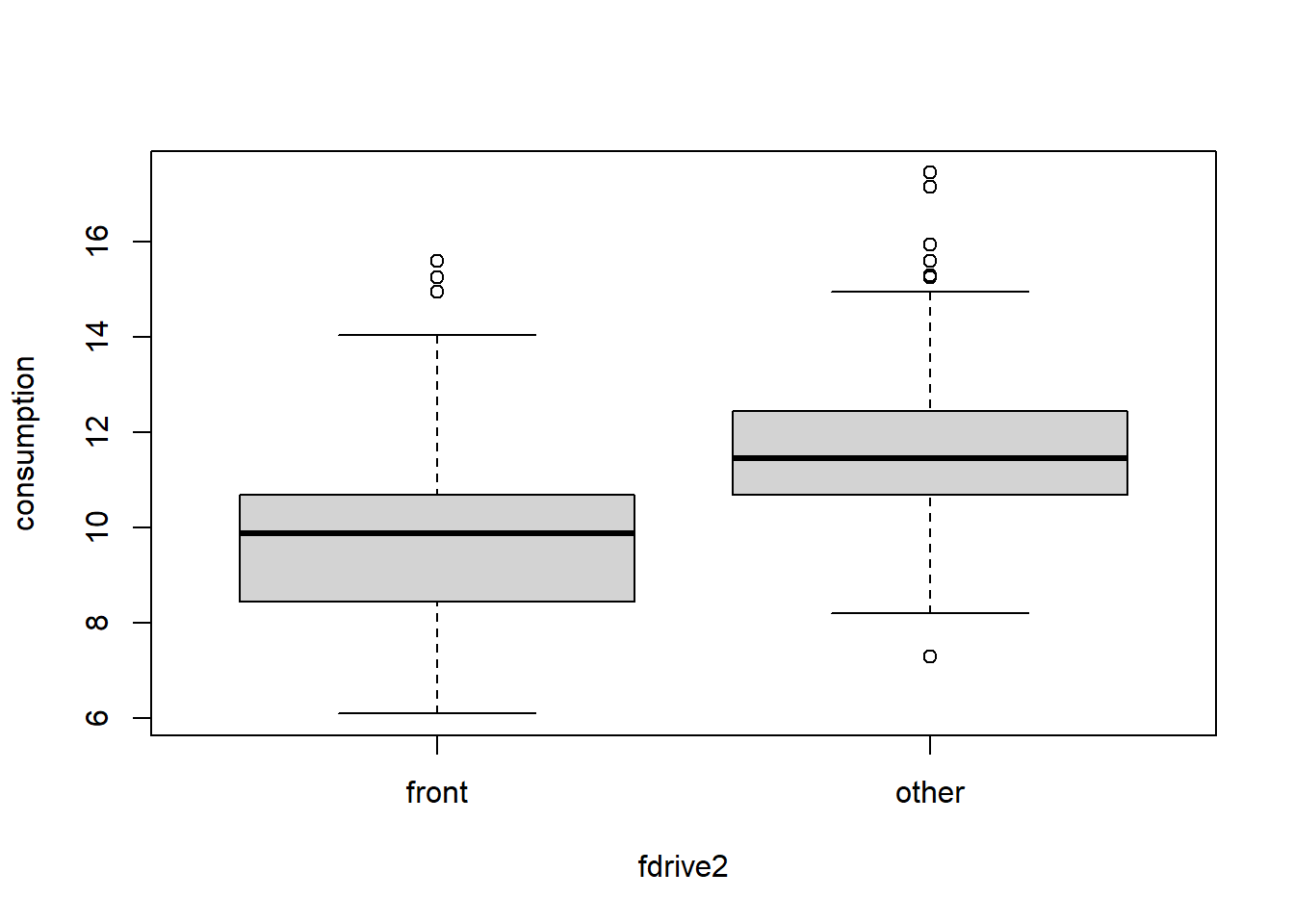
With some effort you can make this plot more compelling:
COL <- c("yellowgreen", "goldenrod")
names(COL) <- levels(Cars2004nh$fdrive2)
par(mfrow = c(1,1), mar = c(4,4,1.5,0.5))
plot(consumption ~ fdrive2, data = Cars2004nh, col = COL,
xlab = "Drive of the vehicle", ylab = "Consumption [l/100 km]",
main = "Consumption vs. Front drive",
cex.main = 1.0,
xaxt = "n")
axis(1, at = 1:nlevels(Cars2004nh$fdrive2), labels = c("Front drive", "Other"))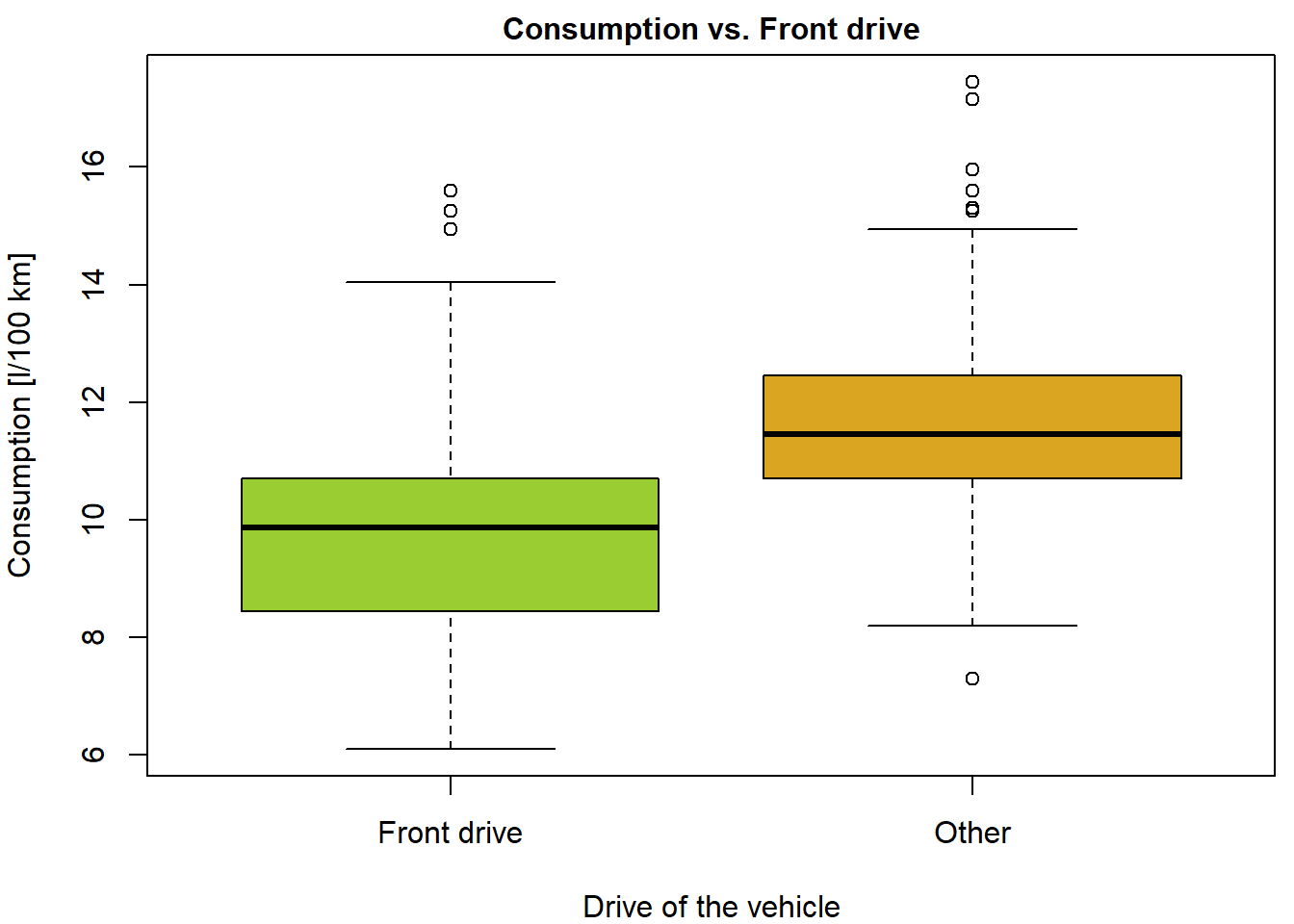
Boxplots of consumption for two categories of drive.
Think about other ways of displaying the two different distributions. Here are the sample characteristics:
with(Cars2004nh, tapply(consumption, fdrive2, summary))## $front
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 6.10 8.45 9.88 9.86 10.70 15.60
##
## $other
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 7.3 10.7 11.4 11.8 12.4 17.4with(Cars2004nh, tapply(consumption, fdrive2, sd, na.rm = TRUE))## front other
## 1.849 1.961X = subset(Cars2004nh, fdrive2 == "front")$consumption
Y = subset(Cars2004nh, fdrive2 == "other")$consumptionFormal statistical test(s)
For each test refresh the following:
- What is the underlying model in each test?
- What are the assumptions?
Standard two-sample t-test (assuming equal variances and normality)
t.test(consumption ~ fdrive2, data = Cars2004nh, var.equal = TRUE)##
## Two Sample t-test
##
## data: consumption by fdrive2
## t = -7.6, df = 218, p-value = 8e-13
## alternative hypothesis: true difference in means between group front and group other is not equal to 0
## 95 percent confidence interval:
## -2.469 -1.454
## sample estimates:
## mean in group front mean in group other
## 9.863 11.825mean(X) - mean(Y)## [1] -1.961Welch two-sample t-test (not assuming equal variances)
t.test(consumption ~ fdrive2, data = Cars2004nh) ##
## Welch Two Sample t-test
##
## data: consumption by fdrive2
## t = -7.6, df = 218, p-value = 7e-13
## alternative hypothesis: true difference in means between group front and group other is not equal to 0
## 95 percent confidence interval:
## -2.468 -1.455
## sample estimates:
## mean in group front mean in group other
## 9.863 11.825Wilcoxon two-sample rank test
wilcox.test(consumption ~ fdrive2, data = Cars2004nh, conf.int = TRUE)##
## Wilcoxon rank sum test with continuity correction
##
## data: consumption by fdrive2
## W = 2548, p-value = 1e-13
## alternative hypothesis: true location shift is not equal to 0
## 95 percent confidence interval:
## -2.30 -1.35
## sample estimates:
## difference in location
## -1.8median(X) - median(Y)## [1] -1.575XYdiff = outer(X, Y, FUN="-")
median(XYdiff)## [1] -1.8Kolmogorov-Smirnov test
ks.test(consumption ~ fdrive2, data = Cars2004nh)##
## Asymptotic two-sample Kolmogorov-Smirnov test
##
## data: consumption by fdrive2
## D = 0.52, p-value = 2e-13
## alternative hypothesis: two-sidedpar(mfrow = c(1,1), mar = c(4,4,1.5,0.5))
plot(ecdf(X), main="ECDF")
plot(ecdf(Y), col=2, add=TRUE)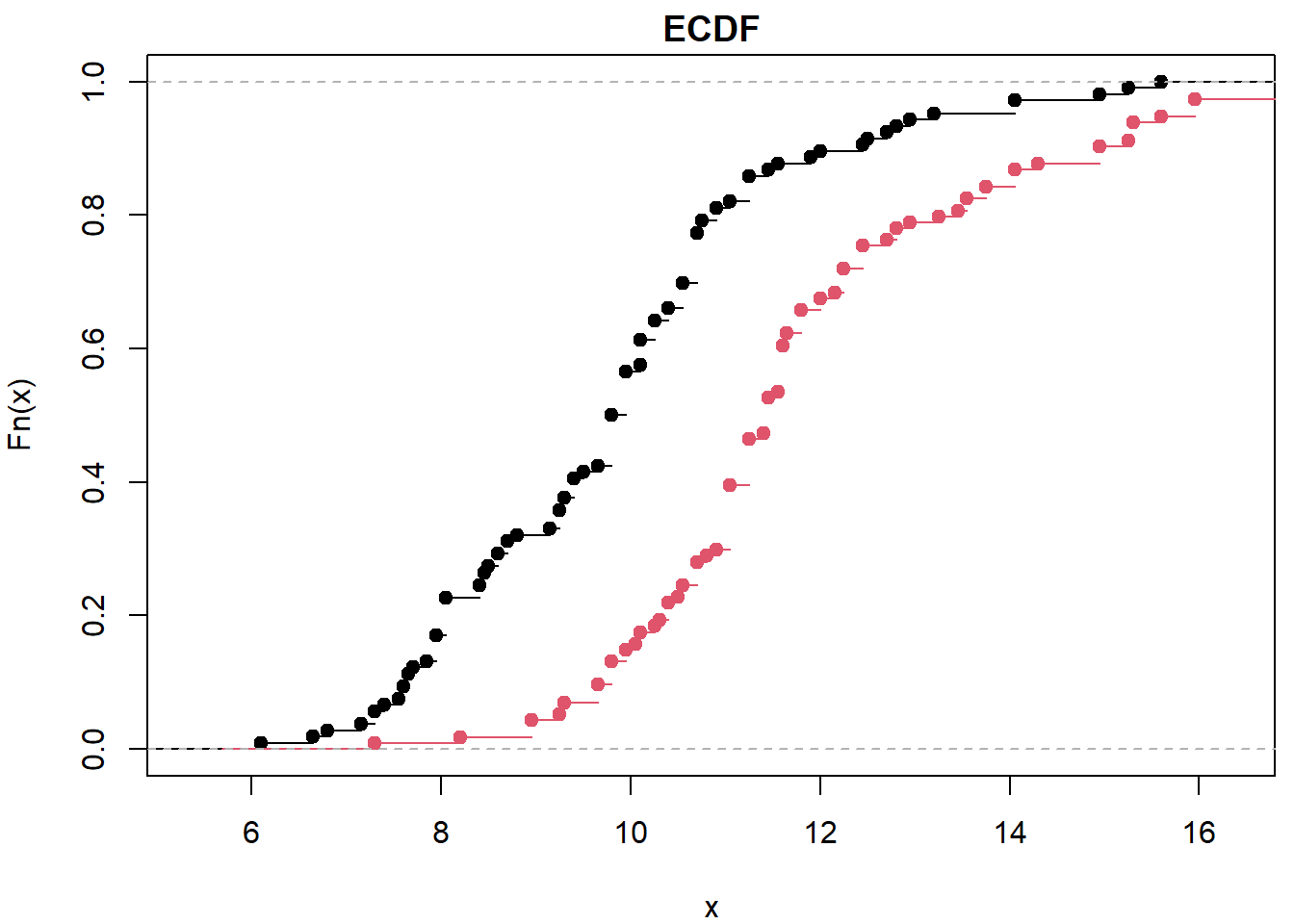
More sample problem
What if there are more than two groups?
Does the consumption depend on the drive (distinguishing front/rear/4x4)?
Exploration
Let’s start with boxplots:
plot(consumption ~ fdrive, data = Cars2004nh)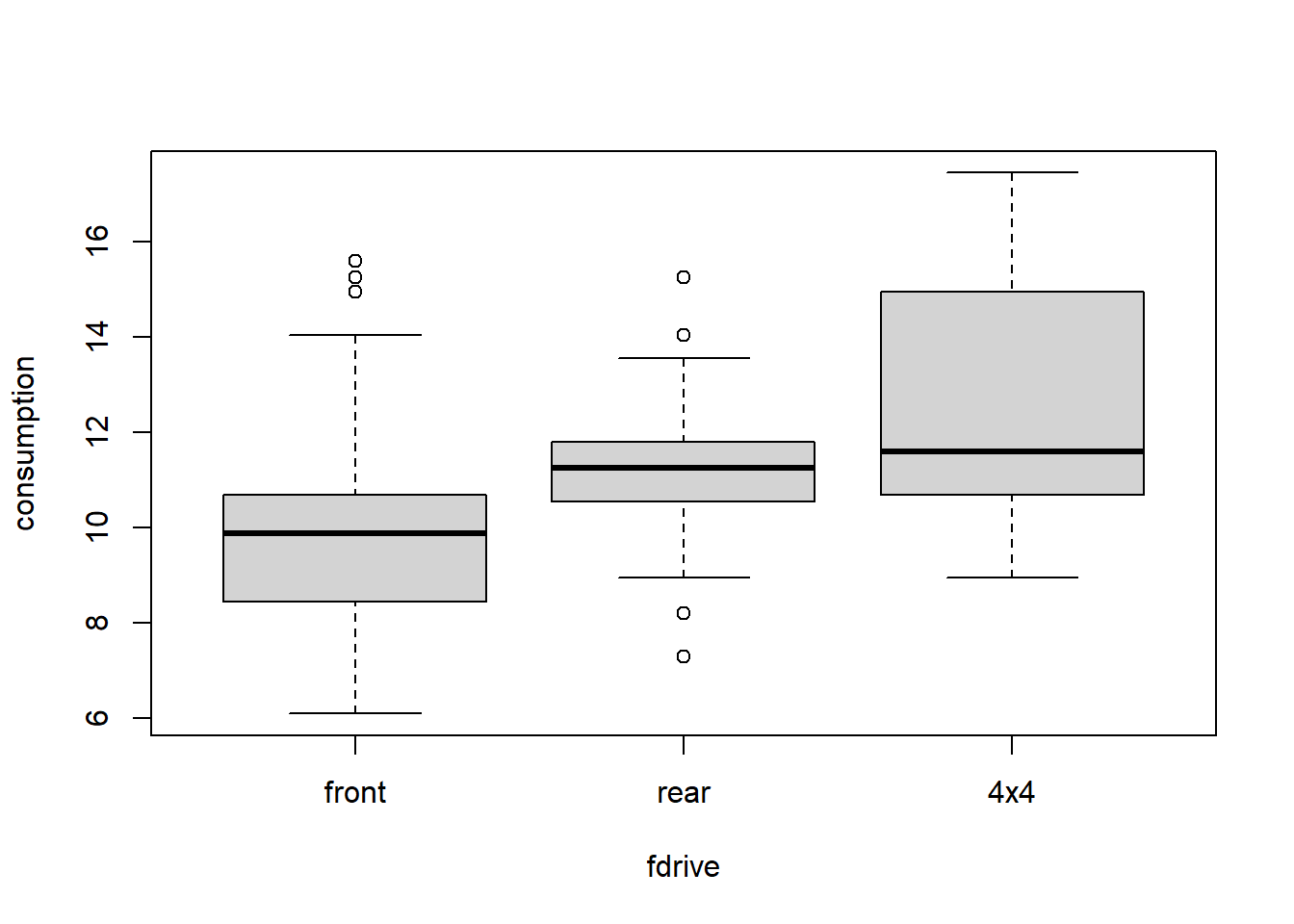
with(Cars2004nh, tapply(consumption, fdrive, summary))## $front
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 6.10 8.45 9.88 9.86 10.70 15.60
##
## $rear
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 7.3 10.6 11.2 11.2 11.8 15.2
##
## $`4x4`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 8.95 10.70 11.60 12.56 14.79 17.45with(Cars2004nh, tapply(consumption, fdrive, sd, na.rm = TRUE))## front rear 4x4
## 1.849 1.360 2.345Formal statistical test(s)
For each test refresh the following:
- What is the underlying model in each test?
- What are the assumptions?
Standard ANOVA
summary(aov(consumption ~ fdrive, data = Cars2004nh)) ## Df Sum Sq Mean Sq F value Pr(>F)
## fdrive 2 260 129.9 37.9 7.9e-15 ***
## Residuals 217 745 3.4
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ANOVA without assuming equal variances
oneway.test(consumption ~ fdrive, data = Cars2004nh) ##
## One-way analysis of means (not assuming equal variances)
##
## data: consumption and fdrive
## F = 31, num df = 2, denom df = 113, p-value = 2e-11Kruskal-Wallis Rank Sum Test
kruskal.test(consumption ~ fdrive, data = Cars2004nh) ##
## Kruskal-Wallis rank sum test
##
## data: consumption by fdrive
## Kruskal-Wallis chi-squared = 58, df = 2, p-value = 2e-13Alternatively: the same test statistics all in the standard ANOVA above
summary(m0 <- lm(consumption ~ fdrive, data=Cars2004nh))##
## Call:
## lm(formula = consumption ~ fdrive, data = Cars2004nh)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.948 -1.313 -0.063 0.912 5.737
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.863 0.180 54.81 < 2e-16 ***
## fdriverear 1.384 0.293 4.72 4.2e-06 ***
## fdrive4x4 2.700 0.318 8.49 3.2e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.85 on 217 degrees of freedom
## Multiple R-squared: 0.259, Adjusted R-squared: 0.252
## F-statistic: 37.9 on 2 and 217 DF, p-value: 7.88e-15anova(m0)## Analysis of Variance Table
##
## Response: consumption
## Df Sum Sq Mean Sq F value Pr(>F)
## fdrive 2 260 129.9 37.9 7.9e-15 ***
## Residuals 217 745 3.4
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1oneway.test(consumption ~ fdrive, data = Cars2004nh, var.equal=TRUE) ##
## One-way analysis of means
##
## data: consumption and fdrive
## F = 38, num df = 2, denom df = 217, p-value = 8e-15Follow these steps to compute the sum of squares and degrees of freedom needed for ANOVA with equal variances:
X = subset(Cars2004nh, fdrive == "front")$consumption
Y = subset(Cars2004nh, fdrive == "rear")$consumption
Z = subset(Cars2004nh, fdrive == "4x4")$consumption
nX = length(X)
nY = length(Y)
nZ = length(Z)
mX = mean(X)
mY = mean(Y)
mZ = mean(Z)
m = mean(c(X,Y,Z))
nX*(m - mX)^2+nY*(m-mY)^2+nZ*(m-mZ)^2## [1] 259.9sum((X - mX)^2)+sum((Y-mY)^2)+sum((Z-mZ)^2)## [1] 744.8sum((c(X,Y,Z)-m)^2)## [1] 1005nX+nY+nZ## [1] 220Conditional mean / Regression
Now we review the basic methods for describing the relationship between two continuous variables.
- Does the consumption depend on the length?
Exploration
Why are boxplots not reasonable choice? Use scatterplot instead,
default for plot between numeric and
numeric variable.
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(consumption ~ length, data = Cars2004nh, col = "red3", bg = "orange", pch = 23)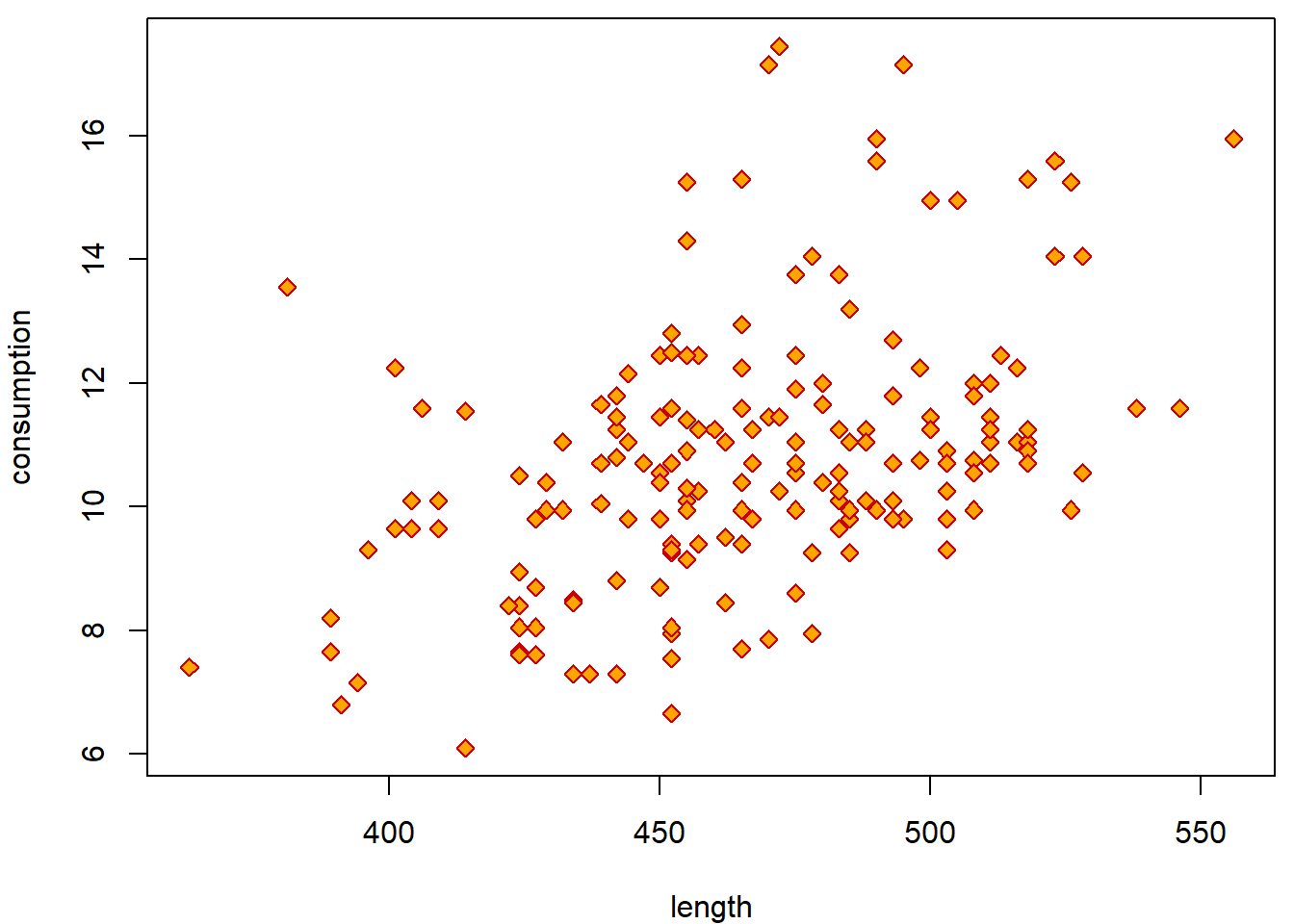
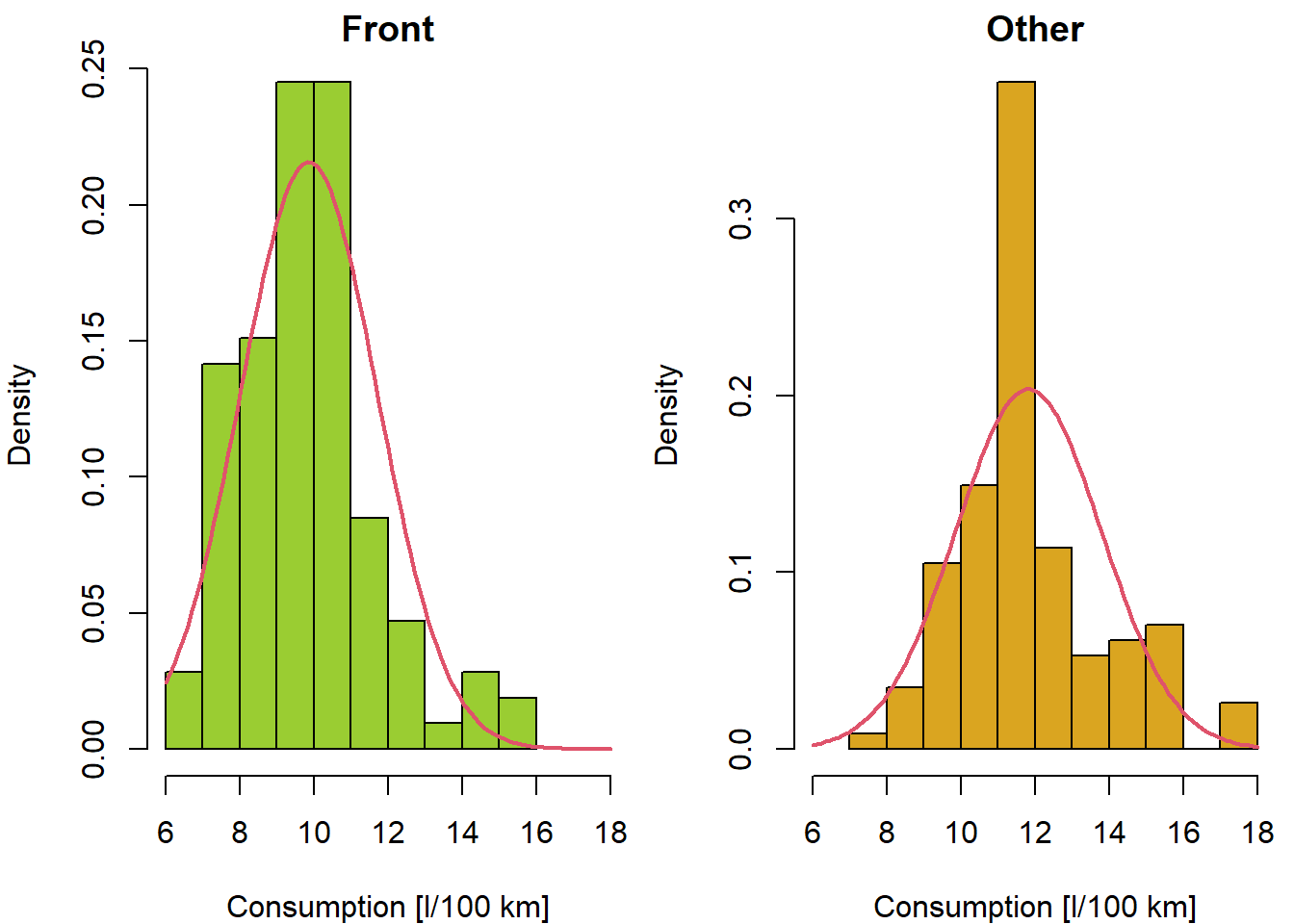
Histograms to inspect the shape of marginal distributions:
### Histograms
par(mfrow = c(1, 2), mar = c(4,4,0.5,0.5))
hist(Cars2004nh$consumption, prob = TRUE, main = "", col = "seagreen",
xlab = "Consumption [l/100 km]")
hist(Cars2004nh$length, prob = TRUE, main = "", col = "seagreen",
xlab = "Length [cm]")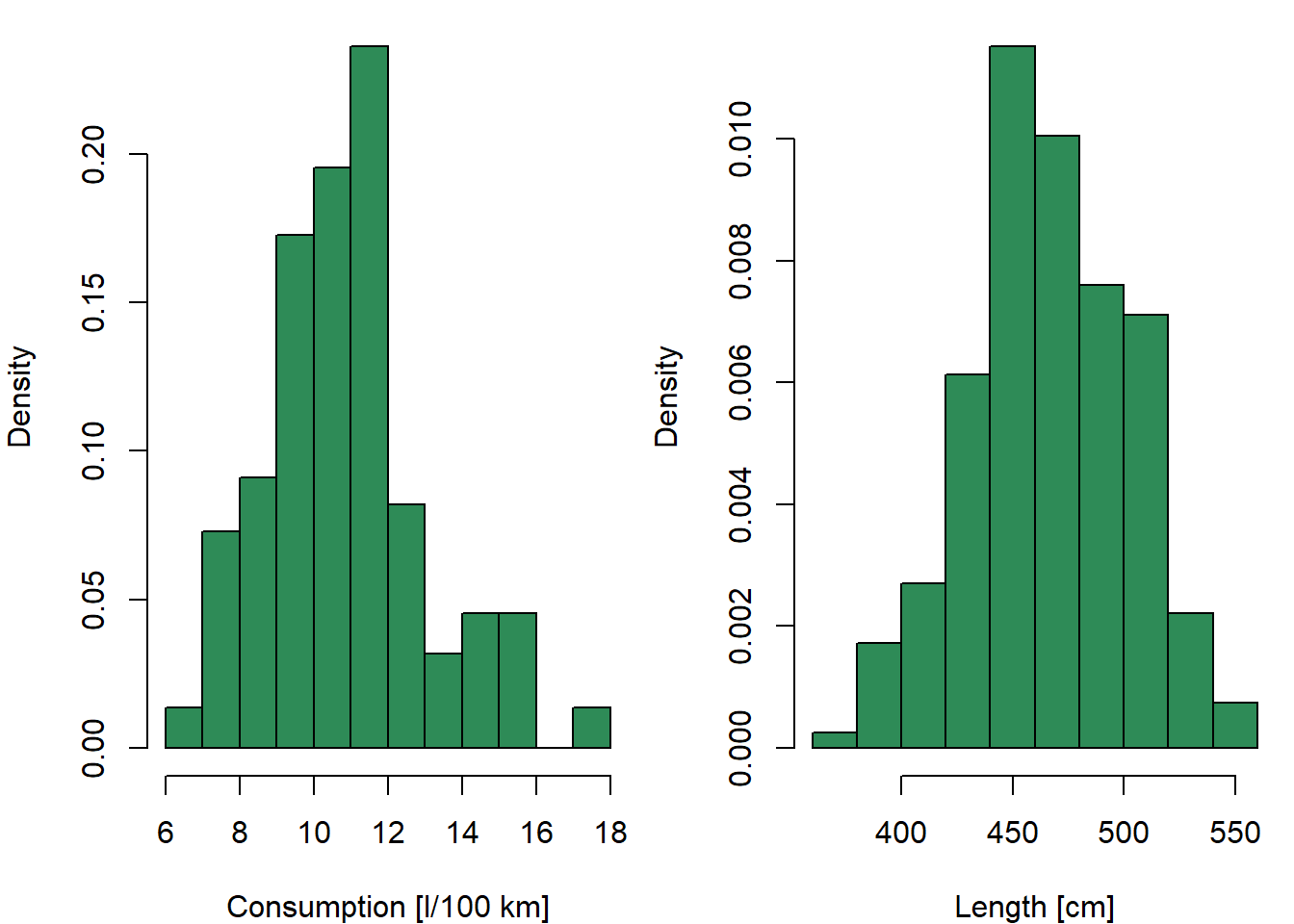
with(Cars2004nh, cor(consumption, length))## [1] NAwith(Cars2004nh, cor(consumption, length, use = "complete.obs"))## [1] 0.438with(Cars2004nh, cor(consumption, length, method = "spearman", use = "complete.obs"))## [1] 0.444Formal statistical test(s)
For each test refresh the following:
- What is the underlying model in each test?
- What are the assumptions?
Test based on Pearson’s correlation coefficient
with(Cars2004nh, cor.test(consumption, length))##
## Pearson's product-moment correlation
##
## data: consumption and length
## t = 6.9, df = 202, p-value = 6e-11
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.3198 0.5427
## sample estimates:
## cor
## 0.438Test based on Spearman’s correlation coefficient
with(Cars2004nh, cor.test(consumption, length, method = "spearman"))##
## Spearman's rank correlation rho
##
## data: consumption and length
## S = 786671, p-value = 3e-11
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.444How would you assess the relationship between the dependent variable and independent covariates?
Here are some graphical tools to examine the (non)linearity of the relationship:
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(consumption ~ length, data = Cars2004nh, col = "red3", bg = "orange", pch = 23)
grid <- quantile(Cars2004nh$length, seq(0, 1, length = 20), na.rm = T)
xGrid <- NULL
yMean <- NULL
for(i in 2:length(grid)){
tempData <- Cars2004nh$consumption[Cars2004nh$length >= grid[i - 1] & Cars2004nh$length < grid[i]]
lines(rep(mean(tempData, na.rm = T), 2) ~ c(grid[i - 1], grid[i]), col = "red")
points((grid[i - 1] + grid[i])/2, mean(tempData, na.rm = T),
pch = 23, bg = "red", cex = 1.2)
xGrid <- c(xGrid, (grid[i - 1] + grid[i])/2)
yMean <- c(yMean, mean(tempData, na.rm = T))
lines(rep(grid[i], 2), c(min(Cars2004nh$consumption), max(Cars2004nh$consumption)), lty = 3)
}
### which interpolates as:
lines(yMean ~ xGrid, col = "darkred", lwd = 3)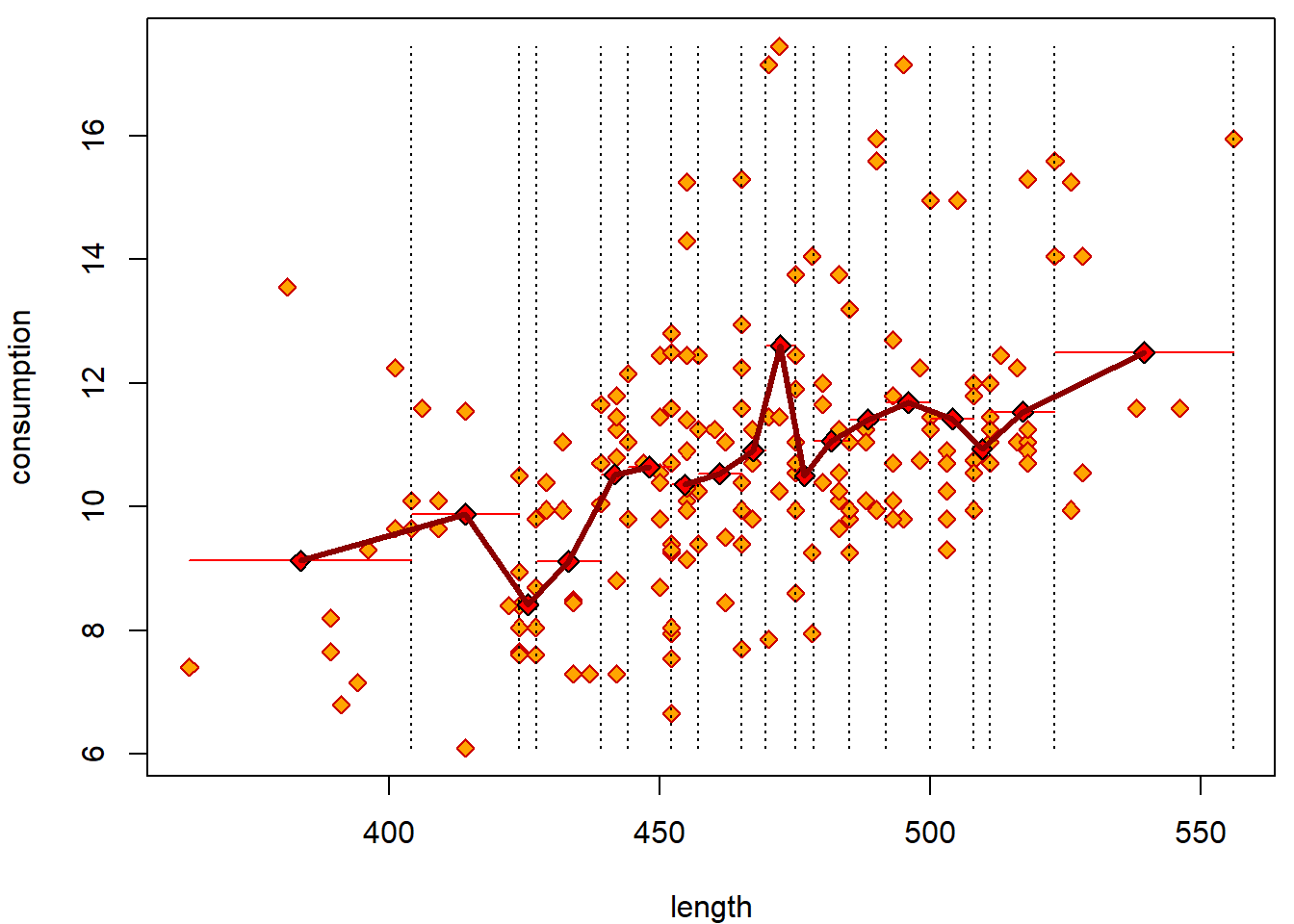
Less groups without for cycle:
grid <- quantile(Cars2004nh$length, seq(0, 1, length = 11), na.rm = T)
Cars2004nh$flength <- cut(Cars2004nh$length, breaks = grid, right = FALSE)
xGrid <- (grid[-1] + grid[-length(grid)]) / 2
yMean <- tapply(Cars2004nh$consumption, Cars2004nh$flength, mean)
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(consumption ~ length, data = Cars2004nh, type = "n")
segments(x0 = grid, y0 = min(Cars2004nh$consumption), y1 = max(Cars2004nh$consumption), lty = 3)
points(consumption ~ length, data = Cars2004nh, col = "red3", bg = "orange", pch = 23)
segments(x0 = grid[-length(grid)], x1 = grid[-1], y0 = yMean, col = "red")
lines(x = xGrid, y = yMean, col = "darkred", lwd = 3)
points(x = xGrid, y = yMean, pch = 23, bg = "red", cex = 1.2)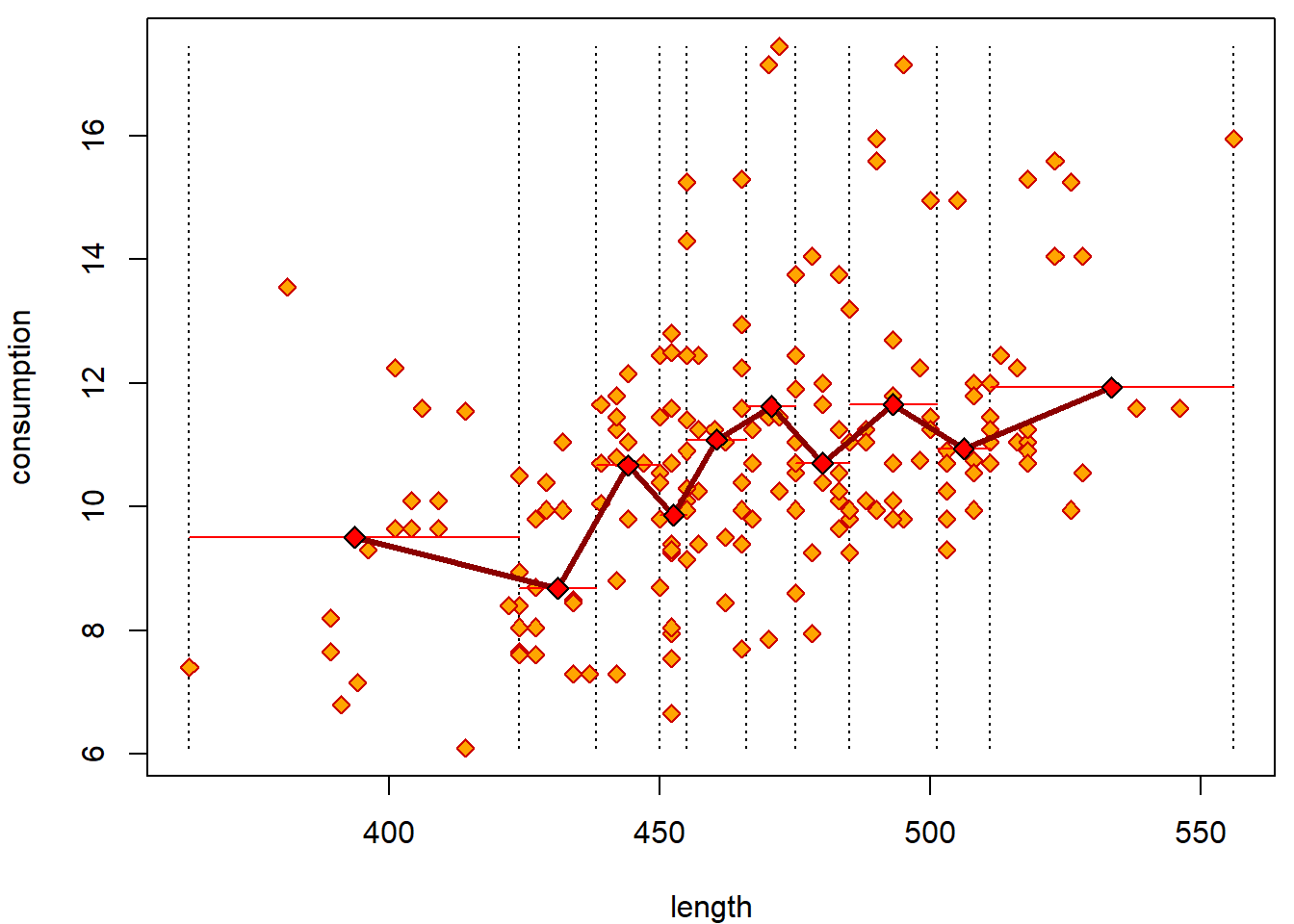
Category for every value of length that appears in the
data:
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(consumption ~ length, data = Cars2004nh, col = "red3", bg = "orange", pch = 23)
grid <- as.numeric(names(table(Cars2004nh$length)))
xGrid <- NULL
yMean <- NULL
for (i in 2:(length(grid) - 1)){
tempData <- Cars2004nh$consumption[Cars2004nh$length >= grid[i - 1] & Cars2004nh$length <= grid[i + 1]]
points(grid[i], mean(tempData, na.rm = T), pch = 23, bg = "red", cex = 1.2)
xGrid <- c(xGrid, grid[i])
yMean <- c(yMean, mean(tempData, na.rm = T))
}
### which now interpolates as:
lines(yMean ~ xGrid, col = "darkred", lwd = 3)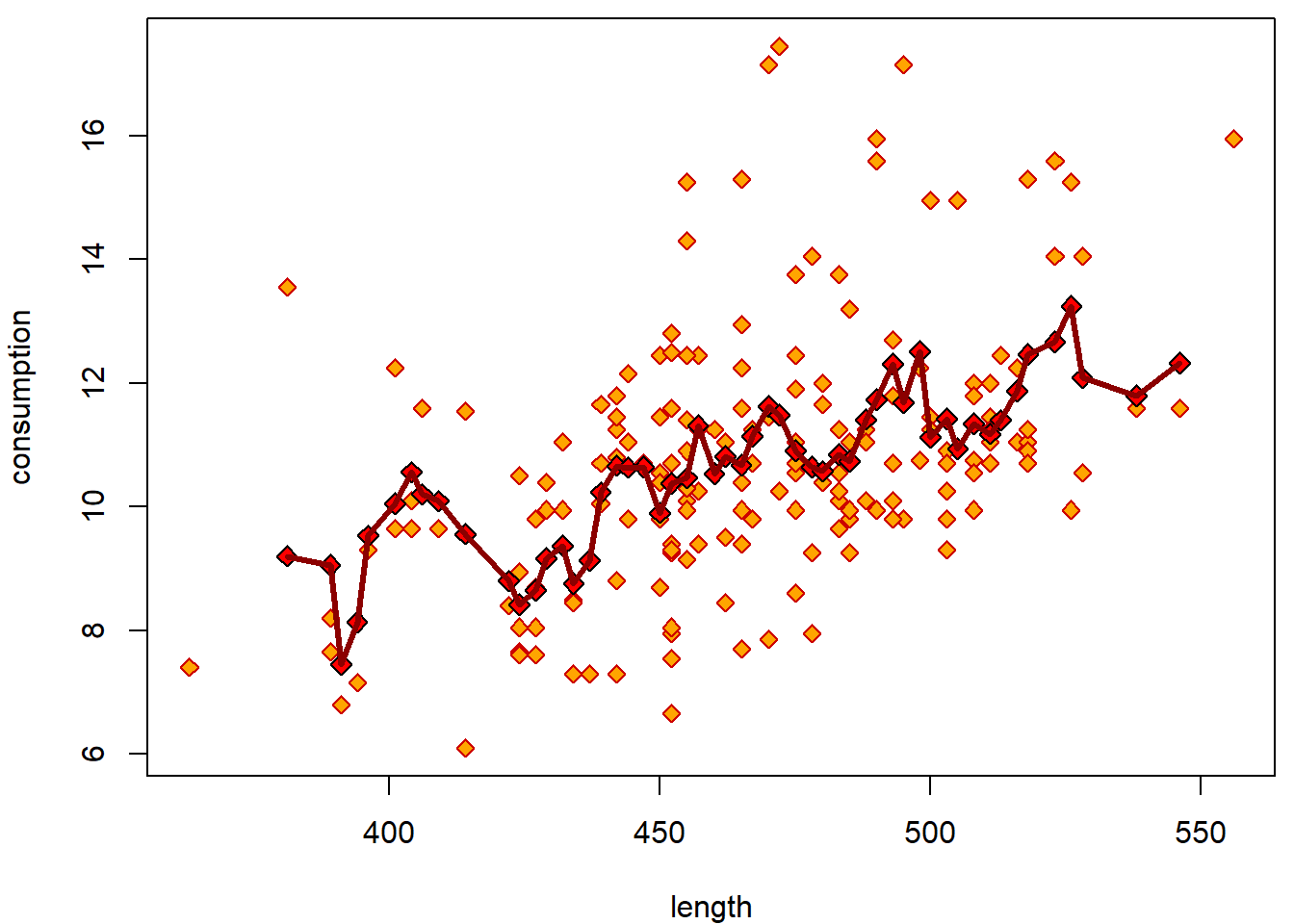
Local trend by lowess curve:
par(mfrow = c(1,3), mar = c(4,4,1.5,0.5))
for(f in c(1/10, 1/5, 1/2)){
plot(consumption ~ length, data = Cars2004nh, col = "red3", bg = "orange",
pch = 23, main = paste0("f = ", f))
tempData <- Cars2004nh[!is.na(Cars2004nh$length),]
lines(lowess(tempData$consumption ~ tempData$length, f = f), col = "red3", lwd = 3)
}
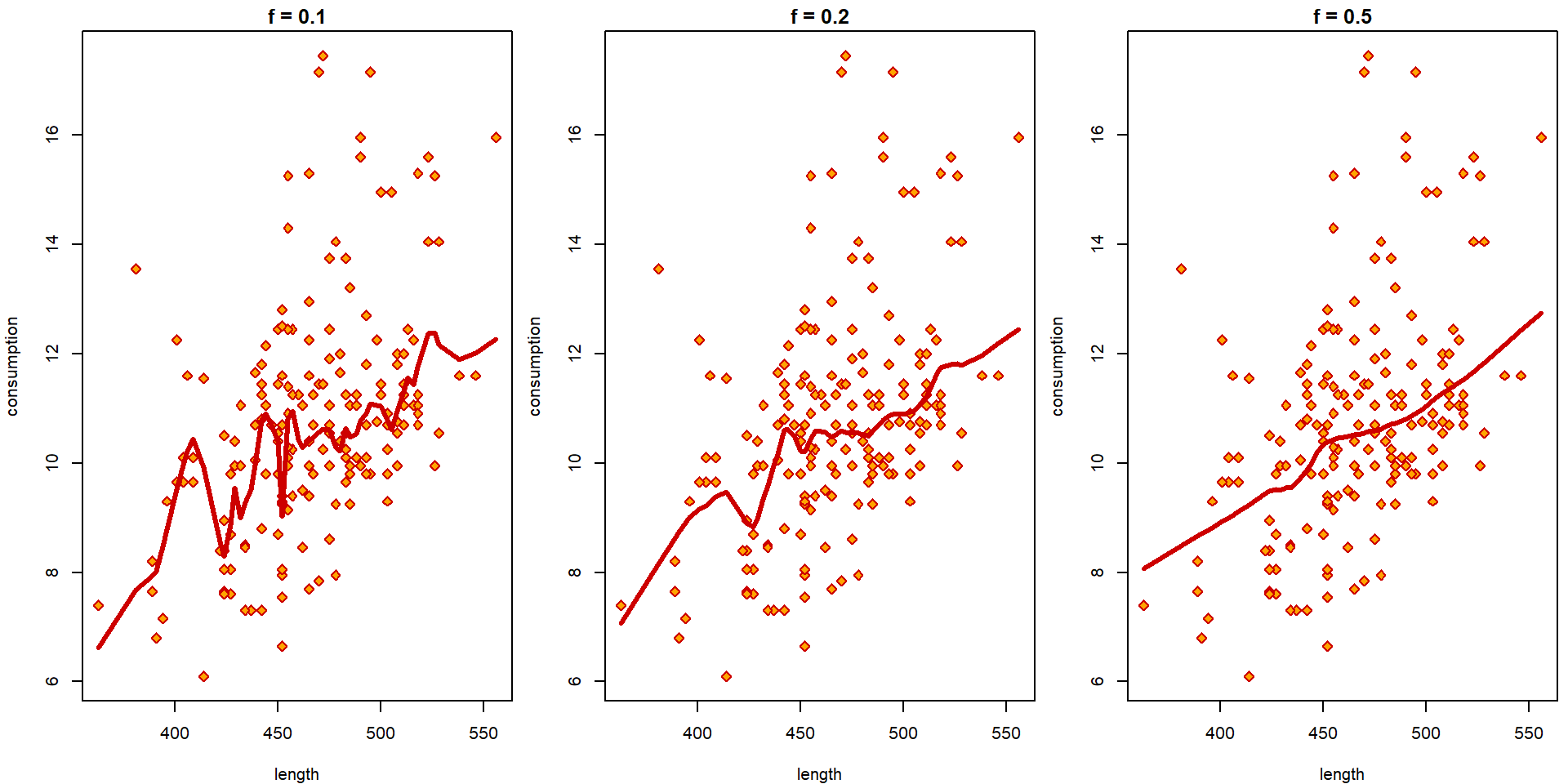How a straight line should be fitted into the data?
Contingency table
We use them to capture the relationship between two categorical variables.
Does the fact that the car is economical (in the U.S. sense,
consumption <= 10) depend on the drive (distinguishing
only front and other)?
Exploration
The default plot for factor ~ factor is the spineplot
that compares the proportions of the first factor within each category
of the second factor separately:
par(mfrow = c(1,1), mar = c(4,4,1,2.5))
plot(fcons10 ~ fdrive2, data = Cars2004nh, col = diverge_hcl(2))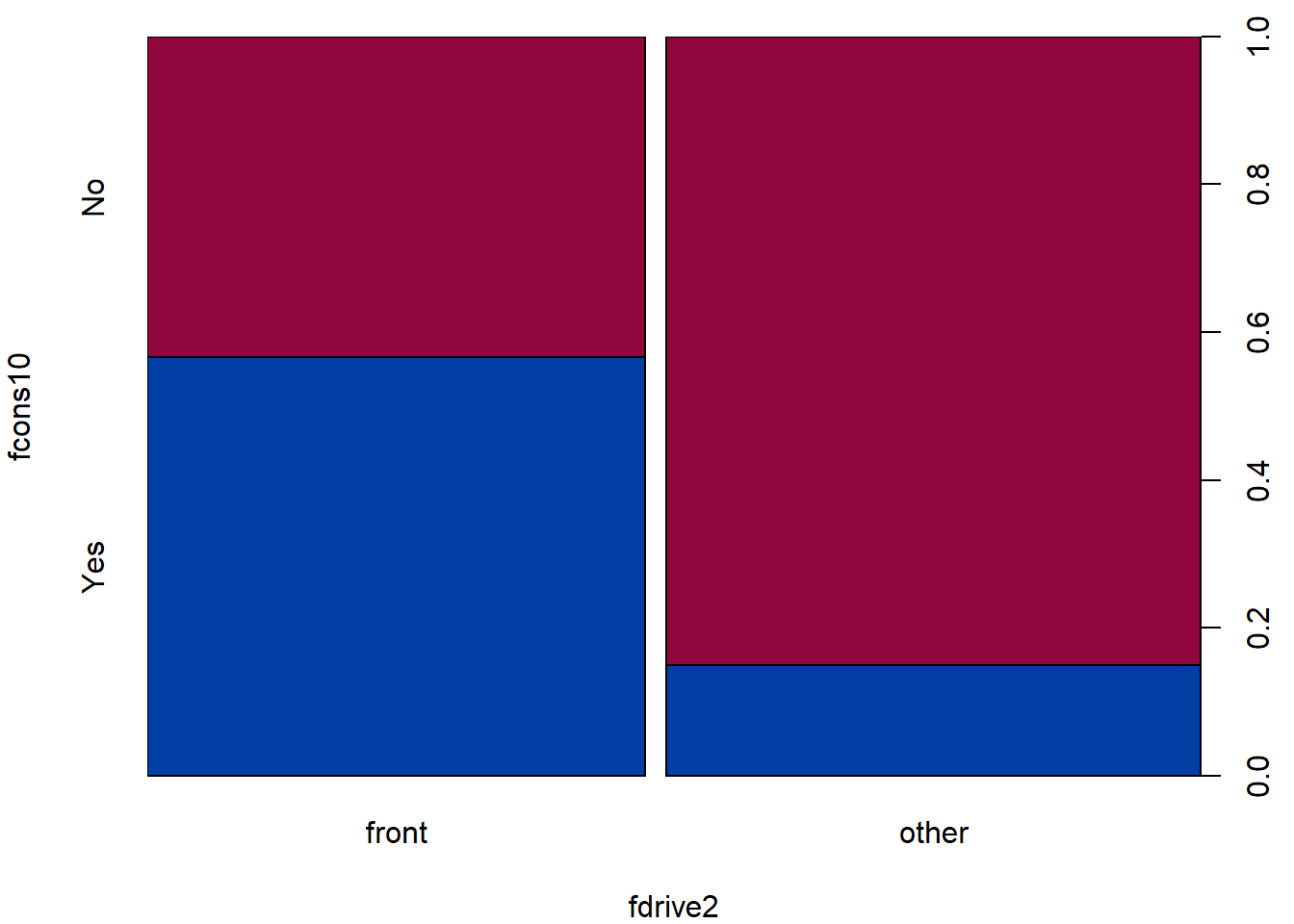
Contingency table:
(TAB2 <- with(Cars2004nh, table(fdrive2, fcons10)))## fcons10
## fdrive2 No Yes
## front 46 60
## other 97 17Proportion table:
round(prop.table(TAB2, margin = 1), 2)## fcons10
## fdrive2 No Yes
## front 0.43 0.57
## other 0.85 0.15Formal statistical test(s)
For each test refresh the following:
- What is the underlying model in each test?
- What are the assumptions?
Chi-square test using continuity correction to be more conservative
chisq.test(TAB2)##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: TAB2
## X-squared = 40, df = 1, p-value = 2e-10Chi-square test without continuity correction
(chi = chisq.test(TAB2, correct = FALSE))##
## Pearson's Chi-squared test
##
## data: TAB2
## X-squared = 42, df = 1, p-value = 9e-11How to obtain the test results manually:
# Expected observed counts under the null hypothesis
print(chi$expected) ## fcons10
## fdrive2 No Yes
## front 68.9 37.1
## other 74.1 39.9n = sum(TAB2) # number of observations
R = rowSums(TAB2)/n # observed proportion in rows
C = colSums(TAB2)/n # observed proportion in columns
R%*%t(C)*n # expected counts under independence## No Yes
## [1,] 68.9 37.1
## [2,] 74.1 39.9(chi$observed - chi$expected)/sqrt(chi$expected) # residuals## fcons10
## fdrive2 No Yes
## front -2.759 3.760
## other 2.660 -3.625chi$residuals## fcons10
## fdrive2 No Yes
## front -2.759 3.760
## other 2.660 -3.625(ts<-sum(chi$res^2)) # test statistic## [1] 41.97pchisq(ts, df=1, lower.tail=FALSE) # p-value## [1] 9.286e-11Test based on difference between proportions. Notice the equivalency
to chisq.test. What can you learn from the output?
(x <- TAB2[, "Yes"])## front other
## 60 17(n <- apply(TAB2, 1, sum))## front other
## 106 114prop.test(x, n)##
## 2-sample test for equality of proportions with continuity correction
##
## data: x out of n
## X-squared = 40, df = 1, p-value = 2e-10
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## 0.2930 0.5408
## sample estimates:
## prop 1 prop 2
## 0.5660 0.1491prop.test(x, n, correct = FALSE)##
## 2-sample test for equality of proportions without continuity correction
##
## data: x out of n
## X-squared = 42, df = 1, p-value = 9e-11
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## 0.3021 0.5317
## sample estimates:
## prop 1 prop 2
## 0.5660 0.1491Reconstruction of the test statistic:
p2 = x/n # proportion estimates in groups
p = sum(x) / sum(n) # common proportion estimate
(ts <- (diff(p2) / sqrt(p*(1-p)*sum(1/n)))^2) # test statistic## other
## 41.97pchisq(ts, df=1, lower.tail=FALSE)## other
## 9.286e-11What is tested here?
prop.test(x, n, alternative = "greater")##
## 2-sample test for equality of proportions with continuity correction
##
## data: x out of n
## X-squared = 40, df = 1, p-value = 1e-10
## alternative hypothesis: greater
## 95 percent confidence interval:
## 0.3115 1.0000
## sample estimates:
## prop 1 prop 2
## 0.5660 0.1491Individual work
Two sample problem
- Verify the assumptions for each two-sample test.
- For instance, a formal test for equal variances in two groups or visual assessment of normality of the two samples.
- How would you visualize the sample means and medians which are tested in the two-sample problems?
More sample problem
- Instead of using three group specific means, consider a reformulation by using the conditional mean given the groups. What is the analogy with the regression formulation?
Contingency tables
- Try also for categorical variables with more than 2 groups.
- Explore the following pairs: (
fcons10,fdrive) and (fdrive,ftype).
For practical purposes one sided alternative can be tested instead. Which alternative makes more sense? What exactly do we test here? Reconstruct the test statistics and the corresponding p-values.
t.test(consumption ~ fdrive2, data = Cars2004nh, alternative = "less", mu = -2)##
## Welch Two Sample t-test
##
## data: consumption by fdrive2
## t = 0.15, df = 218, p-value = 0.6
## alternative hypothesis: true difference in means between group front and group other is less than -2
## 95 percent confidence interval:
## -Inf -1.537
## sample estimates:
## mean in group front mean in group other
## 9.863 11.825t.test(consumption ~ fdrive2, data = Cars2004nh, alternative = "less", mu = -2,
var.equal = TRUE)##
## Two Sample t-test
##
## data: consumption by fdrive2
## t = 0.15, df = 218, p-value = 0.6
## alternative hypothesis: true difference in means between group front and group other is less than -2
## 95 percent confidence interval:
## -Inf -1.536
## sample estimates:
## mean in group front mean in group other
## 9.863 11.825wilcox.test(consumption ~ fdrive2, data = Cars2004nh, alternative = "less",
mu = -2, conf.int = TRUE)##
## Wilcoxon rank sum test with continuity correction
##
## data: consumption by fdrive2
## W = 6410, p-value = 0.8
## alternative hypothesis: true location shift is less than -2
## 95 percent confidence interval:
## -Inf -1.45
## sample estimates:
## difference in location
## -1.8Does the fact that the car is economical (in the U.S. sense,
consumption<=10) depend on the drive (while
distinguishing front, rear or
4x4)?
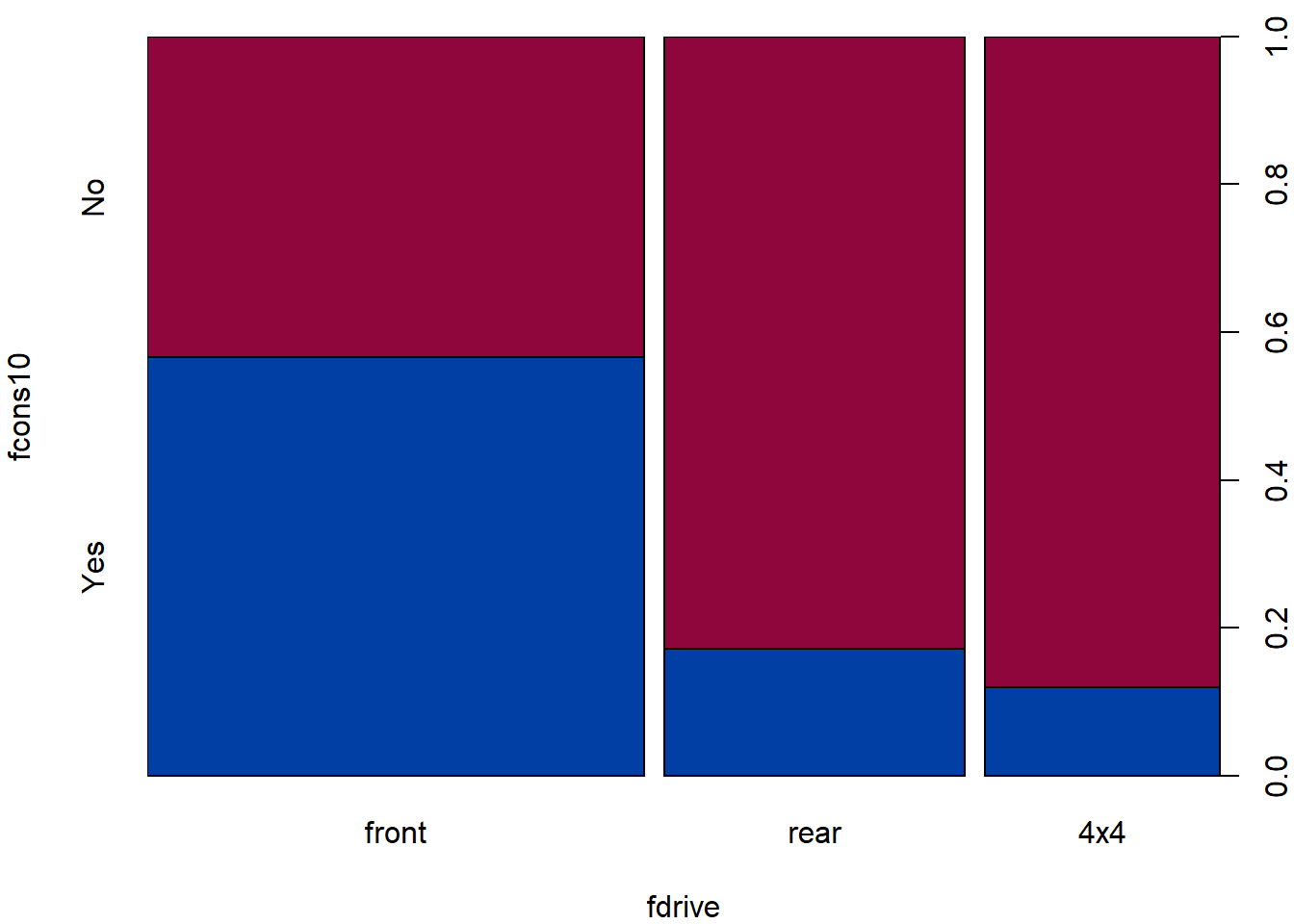
- What are we testing by the following test?
- What is the model behind this test?
- Does the model seem to be good enough to be useful?
- Which artefacts of the model might be relatively safely ignored and why?
- What is the conclusion?
chisq.test(TAB3)##
## Pearson's Chi-squared test
##
## data: TAB3
## X-squared = 42, df = 2, p-value = 7e-10print(chisq.test(TAB3)$expected)## fcons10
## fdrive No Yes
## front 68.9 37.1
## rear 41.6 22.4
## 4x4 32.5 17.5print(chisq.test(TAB3)$residuals)## fcons10
## fdrive No Yes
## front -2.759 3.760
## rear 1.767 -2.409
## 4x4 2.017 -2.749print(chisq.test(TAB3)$stdres)## fcons10
## fdrive No Yes
## front -6.478 6.478
## rear 3.548 -3.548
## 4x4 3.879 -3.879Does the drive (front/rear/4x4) depend on the type of the car (personal/wagon/SUV/pickup/sport/minivan)?
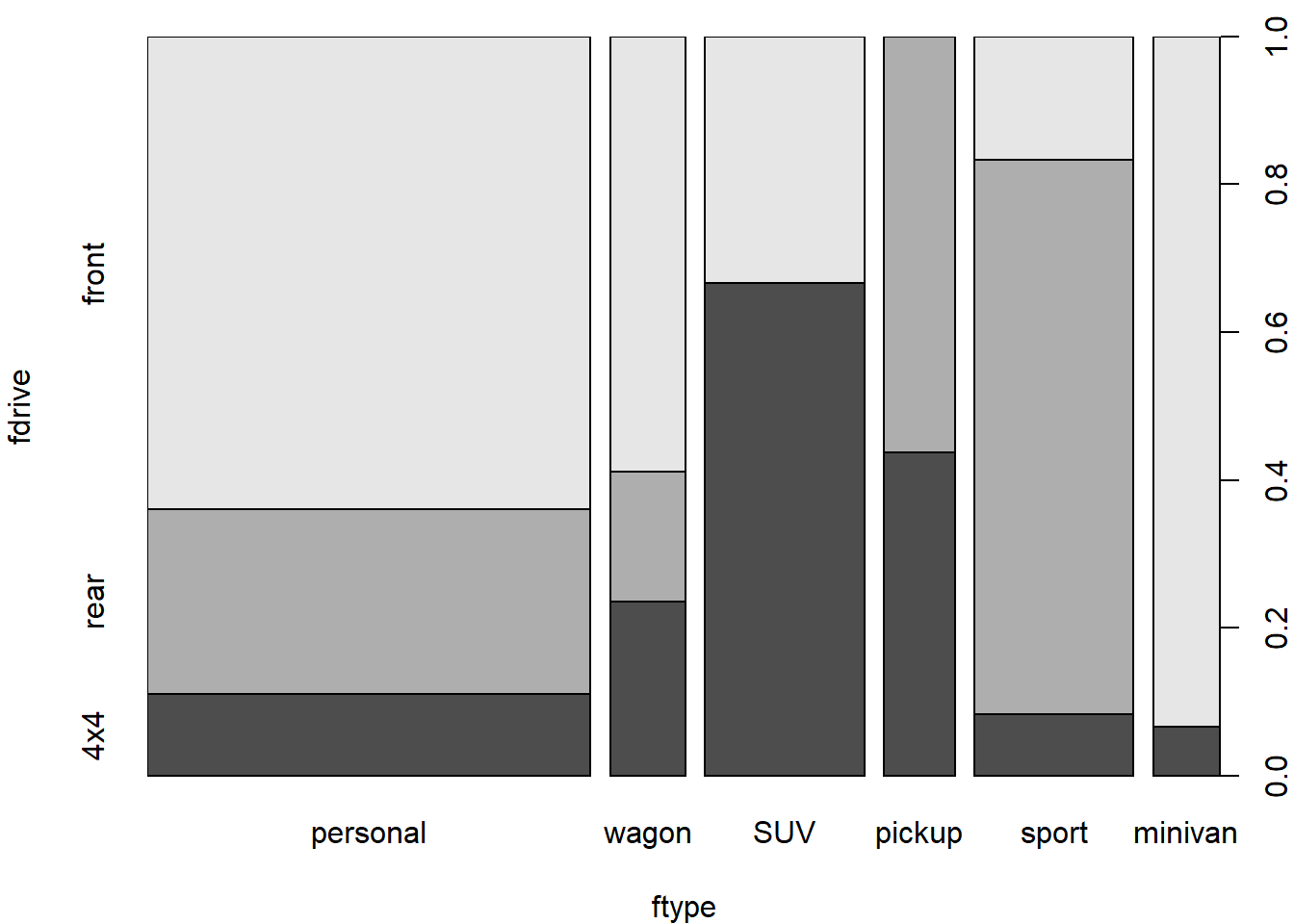
- What are we testing by the following test?
- What is the model behind this test?
- Does the model seem to be good enough to be useful?
- Which artefacts of the model might be relatively safely ignored and why?
- What is the conclusion?
- Why did we get the warning message? What can be done about it?
chisq.test(TAB4)##
## Pearson's Chi-squared test
##
## data: TAB4
## X-squared = 120, df = 10, p-value <2e-16print(chisq.test(TAB4)$expected)## fdrive
## ftype front rear 4x4
## personal 48.182 29.091 22.727
## wagon 8.191 4.945 3.864
## SUV 17.345 10.473 8.182
## pickup 7.709 4.655 3.636
## sport 17.345 10.473 8.182
## minivan 7.227 4.364 3.409