Download this R markdown as: R, Rmd.

Outline of the lab session

Loading the data and libraries

The dataset mtcars (available under the standard R installation) will be used for the purposes of this lab session. Some insight about the data can be taken from the help session (command ?mtcars) or from some outputs provided below.

library(colorspace)
head(mtcars)
##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1
str(mtcars)
## 'data.frame':    32 obs. of  11 variables:
##  $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
##  $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
##  $ disp: num  160 160 108 258 360 ...
##  $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
##  $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
##  $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
##  $ qsec: num  16.5 17 18.6 19.4 17 ...
##  $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
##  $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
##  $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
##  $ carb: num  4 4 1 1 2 1 4 2 2 4 ...
summary(mtcars)
##       mpg            cyl            disp             hp             drat            wt            qsec     
##  Min.   :10.4   Min.   :4.00   Min.   : 71.1   Min.   : 52.0   Min.   :2.76   Min.   :1.51   Min.   :14.5  
##  1st Qu.:15.4   1st Qu.:4.00   1st Qu.:120.8   1st Qu.: 96.5   1st Qu.:3.08   1st Qu.:2.58   1st Qu.:16.9  
##  Median :19.2   Median :6.00   Median :196.3   Median :123.0   Median :3.69   Median :3.33   Median :17.7  
##  Mean   :20.1   Mean   :6.19   Mean   :230.7   Mean   :146.7   Mean   :3.60   Mean   :3.22   Mean   :17.8  
##  3rd Qu.:22.8   3rd Qu.:8.00   3rd Qu.:326.0   3rd Qu.:180.0   3rd Qu.:3.92   3rd Qu.:3.61   3rd Qu.:18.9  
##  Max.   :33.9   Max.   :8.00   Max.   :472.0   Max.   :335.0   Max.   :4.93   Max.   :5.42   Max.   :22.9  
##        vs              am             gear           carb     
##  Min.   :0.000   Min.   :0.000   Min.   :3.00   Min.   :1.00  
##  1st Qu.:0.000   1st Qu.:0.000   1st Qu.:3.00   1st Qu.:2.00  
##  Median :0.000   Median :0.000   Median :4.00   Median :2.00  
##  Mean   :0.438   Mean   :0.406   Mean   :3.69   Mean   :2.81  
##  3rd Qu.:1.000   3rd Qu.:1.000   3rd Qu.:4.00   3rd Qu.:4.00  
##  Max.   :1.000   Max.   :1.000   Max.   :5.00   Max.   :8.00

1. Multiple linear regression model

For simplicity, we will only consider three explanatory (continuous) variables from the whole mtcars dataset, i.e. \(\boldsymbol{x} \in \mathbb{R}^3\). Any generalization for general \(\boldsymbol{X} \in \mathbb{R}^p\) for some \(p \in \mathbb{N}\) is straightforward. In particular, the (continuous) dependent variable \(Y \in \mathbb{R}\) is the car consumption (variable in the dataset denoted as mpg – miles per gallon) and three independent variables will be the car’s displacement (disp), horse powers (hp), and the rear axle ratio information (drat).

Three simple scatterplots showing the dependent variable \(Y\) against one independent variable (based on the random sample \(\{(Y_i, \boldsymbol{X}_i^\top)^\top;~i = 1, \dots, 32\}\)) are shown below. Only a limited information about the whole multivariate structure of the underlying data can be, howver, taken from the series of two-dimensional scatterplots.

par(mfrow = c(1,3), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", 
     ylab = "Miles per gallon", xlab = "Displacement [cubic inches]")
lines(lowess(mtcars$mpg ~ mtcars$disp), col = "red", lwd = 2)
plot(mpg ~ hp, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", 
     ylab = "", xlab = "Horse Power")
lines(lowess(mtcars$mpg ~ mtcars$hp), col = "red", lwd = 2)
plot(mpg ~ drat, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", 
     ylab = "", xlab = "Rear axle ratio")
lines(lowess(mtcars$mpg ~ mtcars$drat), col = "red", lwd = 2)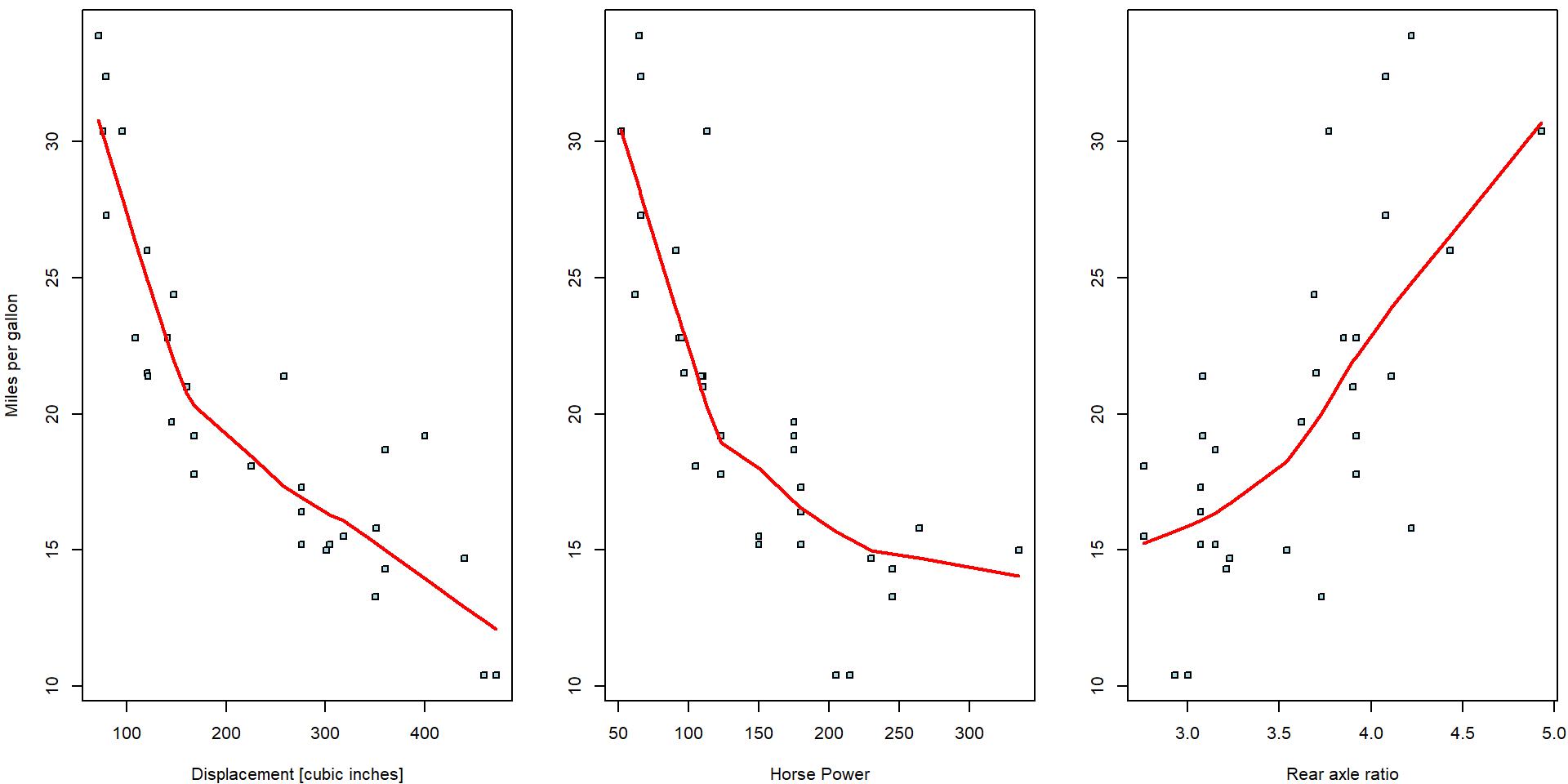

The red curves are non-parametric estimates of the conditional mean—these estimates offer a useful insight that the dependence of the consumptions is very likely negative (regressive) wrt. the displacement and horsepower while it seems to positive (progressive) for the rear axle ratio.

A simple multiple regression model of the form \[ Y = \beta_0 + \beta_1 \mathtt{disp} + \beta_2\mathtt{hp} + \beta_3 \mathtt{drat} + \varepsilon \] or mathematically (the model for the empirical data, for \(i = 1, \dots, 32\)) \[ Y_i = \boldsymbol{X}_i^\top\boldsymbol{\beta} + \varepsilon_i \] where \(\boldsymbol{X} = (1, \mathtt{disp}, \mathtt{hp}, \mathtt{drat})^\top\) and \(\boldsymbol{\beta} \in \mathbb{R}^4\) will be considered. In the R software, the model can be fitted using the following R code:

fit1 <- lm(mpg ~ disp + hp + drat, data = mtcars)
print(fit1)
## 
## Call:
## lm(formula = mpg ~ disp + hp + drat, data = mtcars)
## 
## Coefficients:
## (Intercept)         disp           hp         drat  
##     19.3443      -0.0192      -0.0312       2.7150

The information in the output above gives values for four estimated parameters – elements of the parameter vector \(\boldsymbol{\beta} \in \mathbb{R}^4\). The estimated parameters are not the same as estimated three independent simple linear regression model. Compare the output above with the following outputs:

fit_disp <- lm(mpg ~ disp, data = mtcars)
fit_hp <- lm(mpg ~ hp, data = mtcars)
fit_drat <- lm(mpg ~ drat, data = mtcars)

print(fit_disp)
## 
## Call:
## lm(formula = mpg ~ disp, data = mtcars)
## 
## Coefficients:
## (Intercept)         disp  
##     29.5999      -0.0412
print(fit_hp)
## 
## Call:
## lm(formula = mpg ~ hp, data = mtcars)
## 
## Coefficients:
## (Intercept)           hp  
##     30.0989      -0.0682
print(fit_drat)
## 
## Call:
## lm(formula = mpg ~ drat, data = mtcars)
## 
## Coefficients:
## (Intercept)         drat  
##       -7.52         7.68

Indeed, while the signs of the estimated parameters correspond, the magnitudes are substantially different. The ordinary regressions can be directly plotted into the corresponding scatterplots:

par(mfrow = c(1,3), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", ylab = "Miles per gallon", xlab = "Displacement [cubic inches]")
lines(lowess(mtcars$mpg ~ mtcars$disp), col = "red", lwd = 2)
abline(fit_disp, col = "blue")
plot(mpg ~ hp, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", ylab = "", xlab = "Horse Power")
lines(lowess(mtcars$mpg ~ mtcars$hp), col = "red", lwd = 2)
abline(fit_hp, col = "blue")
plot(mpg ~ drat, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", ylab = "", xlab = "Rear axle ratio")
lines(lowess(mtcars$mpg ~ mtcars$drat), col = "red", lwd = 2)
abline(fit_drat, col = "blue")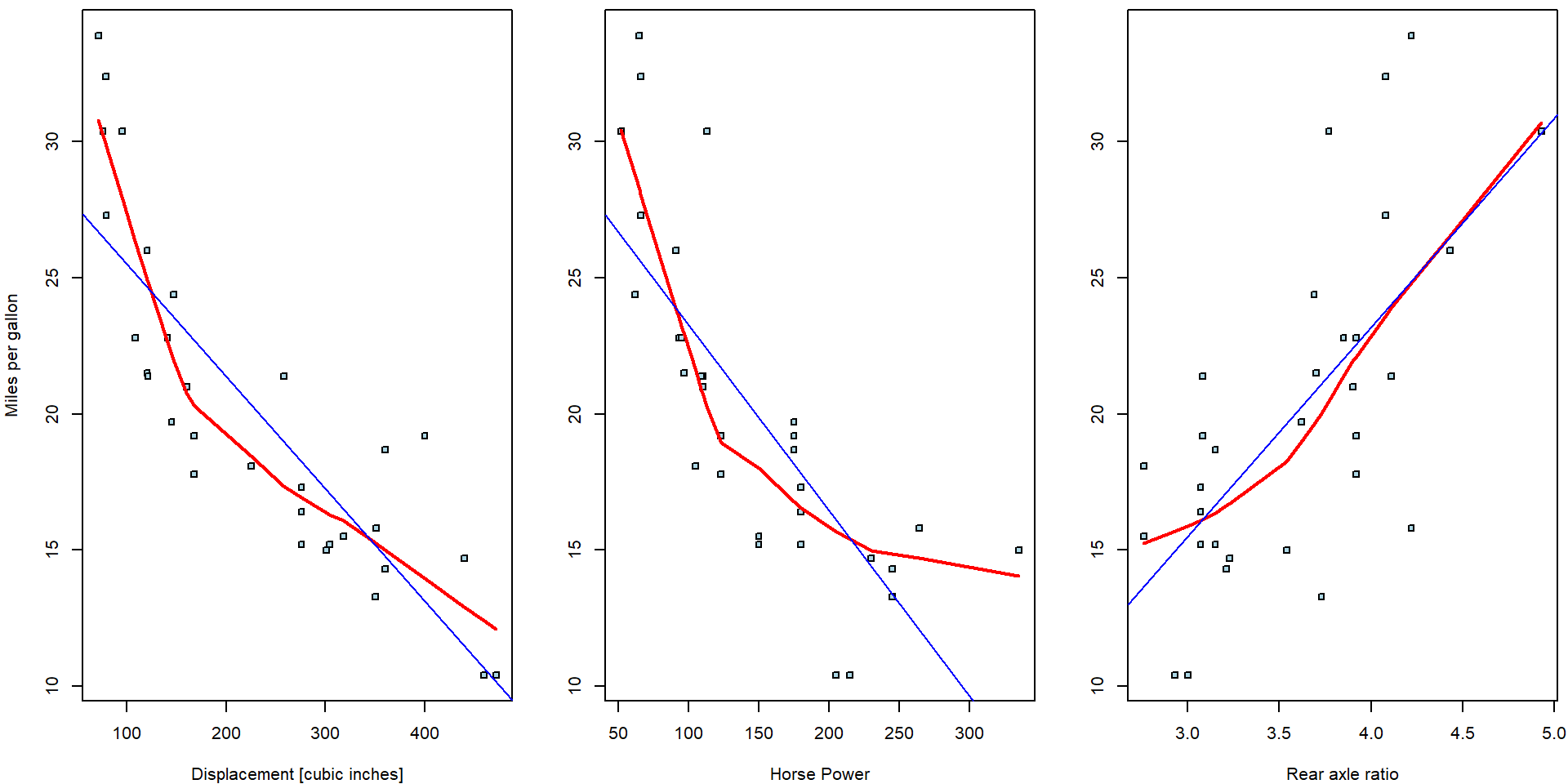

However, the multiple regression model does not estimate a line but a three dimensional subspace. For instance, the intercept value \(\widehat{\beta}_0 = 29.6\) from the simple regression model fit_disp stands for the expected driven miles per one gallon if the displacement of the engine is equal to zero cubic inches (i.e., an unrealistic scenario).

Nevertheless, the intercept estimate \(\widehat{\beta}_0 = 19.34\) stands for the expected driven miles per one gallon but if all three regressors – the information about the displacement, the horse powers, and, also, the rear to axel ratio – are all equal to zero. Therefore, to draw simple line for two-dimensional scatterplot, it is needed to pre-select some reasonable information (realistic case) for all other covariates in the model.

For instance, consider the multiple model from above and, in particular, the scatterplot of the consumption against the displacement. Various regression lines can be considered:

par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", 
     xlab = "Displacement [cubic inches]", ylab = "Miles per gallon")

xGrid <- seq(min(mtcars$disp), max(mtcars$disp, 100))
mCoeff <- fit1$coeff

yMeanMean <- mCoeff[1] + mCoeff[2] * xGrid + mCoeff[3] * mean(mtcars$hp) + mCoeff[4] * mean(mtcars$drat) 
lines(yMeanMean ~ xGrid, col = "red", lwd = 2)

yMinMin <- mCoeff[1] + mCoeff[2] * xGrid + mCoeff[3] * min(mtcars$hp) + mCoeff[4] * min(mtcars$drat) 
yMaxMax<- mCoeff[1] + mCoeff[2] * xGrid + mCoeff[3] * max(mtcars$hp) + mCoeff[4] * max(mtcars$drat) 
lines(yMinMin ~ xGrid, col = "blue", lwd = 2, lty = 2)
lines(yMaxMax ~ xGrid, col = "darkgreen", lwd = 2, lty = 2)

legend("topright", 
       legend = c("Average HP & average rear axle ratio", 
                  "Min HP & min rear axle ratio", 
                  "Max HP & max rear axle ratio"), 
       col =c("red", "blue", "darkgreen"), lwd = c(3,3,3), lty = c(1,2,2))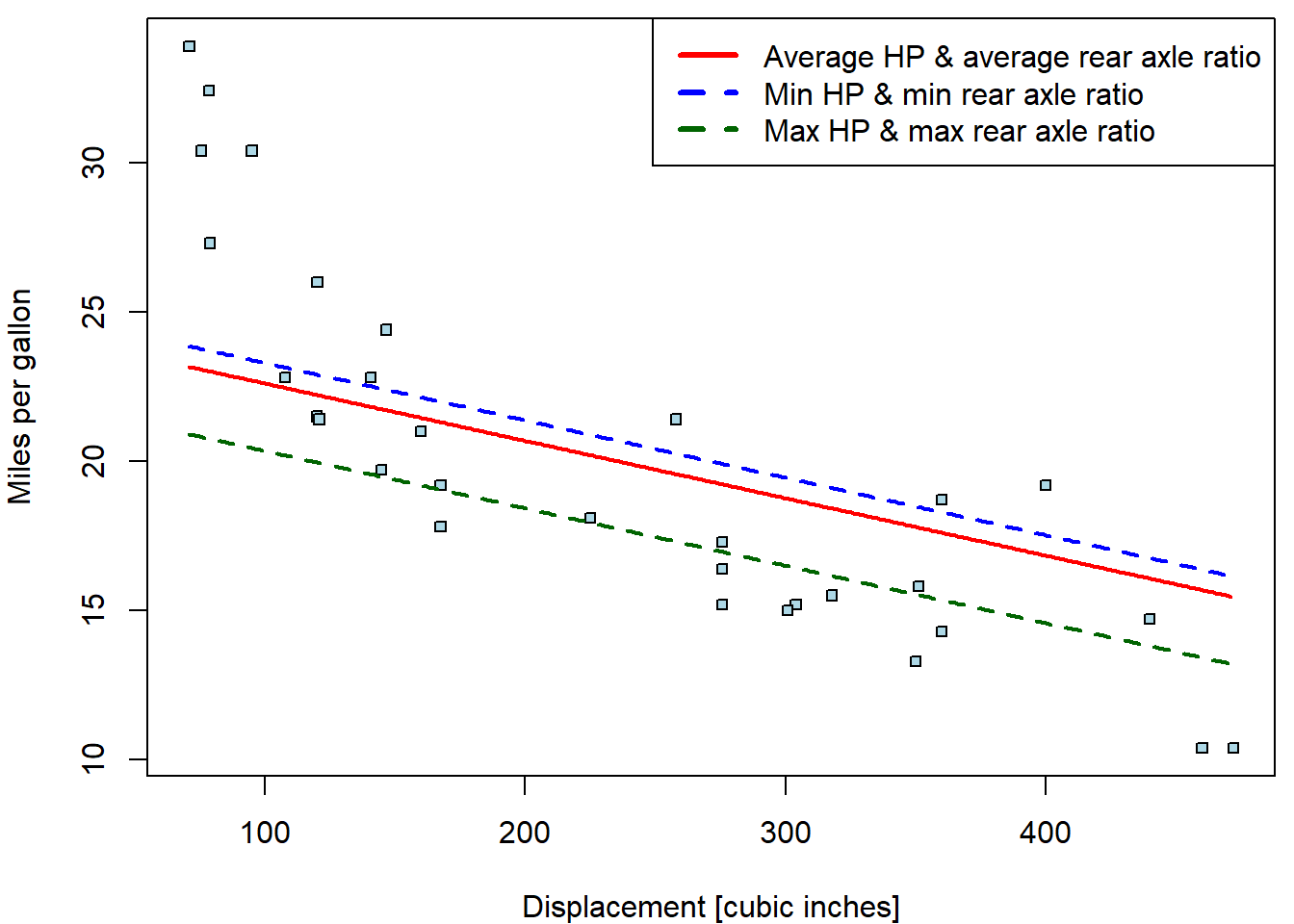

Individual work

2. Basic inference on \(\boldsymbol{\beta} \in \mathbb{R}^p\)

The main purpose of statistic is to do inference – i.e., to say something relevant about the whole (unknown) population (from which we have a small random sample \(\{(Y_i, \boldsymbol{X}_i^\top)^\top;~i = 1, \dots, 32\}\)) using only the information (data) in the sample and the techniques of statistical inference. There are two main tools for the statistical inference – confidence intervals for the unknown parameters and the hypothesis tests.

While the confidence intervals must be calculated manually – however, using just the standard output from the regression model – some statistical tests are provided automatically. A statistical output of the multiple linear regression model fitted above can be obtained by the command summary():

summary(fit1)
## 
## Call:
## lm(formula = mpg ~ disp + hp + drat, data = mtcars)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -5.122 -1.845 -0.446  1.134  6.496 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept) 19.34429    6.37088    3.04   0.0051 **
## disp        -0.01923    0.00937   -2.05   0.0496 * 
## hp          -0.03123    0.01334   -2.34   0.0266 * 
## drat         2.71498    1.48737    1.83   0.0786 . 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.01 on 28 degrees of freedom
## Multiple R-squared:  0.775,  Adjusted R-squared:  0.751 
## F-statistic: 32.2 on 3 and 28 DF,  p-value: 3.28e-09

Four (the number of estimated parameters) statistical tests – \(p\)-values of the tests are provided in the output (the fourth column of the table) by default. In each case, the corresponding null hypothesis states that the estimated parameter (not the estimate, but the unknown true value) is equal to zero, i.e.,

\[ H_0: \beta_j = 0 \] against a general alternative \[ H_A: \beta_j \neq 0 \] where \(j \in \{1, 2, 3, 4\}\) corresponds to the line in the output table, respectively the element of the estimated parameter vector \(\boldsymbol{\beta} \in \mathbb{R}^4\).

Individual work

3. K-variate parametrizations of a numeric covariate

On previous exercise class we considered transformations that changed a single covariate into another single covariate. These are typically:

But one covariate could be parametrized by more than 1 column! Typical examples:

Consider again the relationship between consumption and displacement:

par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, pch = 22, cex = 0.8, bg = "lightblue", ylab = "Miles per gallon", xlab = "Displacement [cubic inches]")
lines(lowess(mtcars$mpg ~ mtcars$disp), col = "red", lwd = 2)
abline(fit_disp, col = "blue")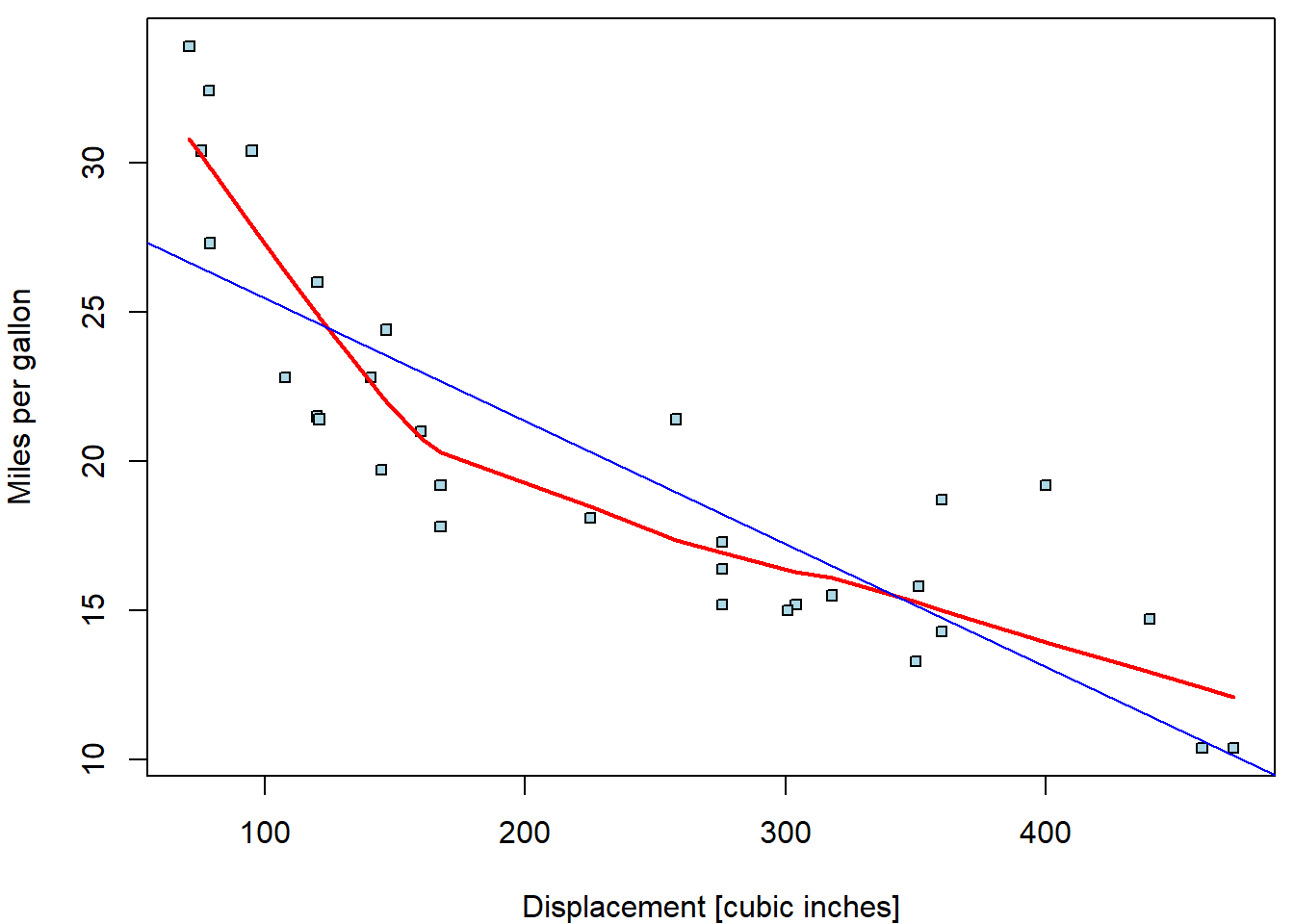

Apparently, linear trend describes the relationship poorly. The lowess curve suggests more concave behaviour. Let us consider other possible parametrizations (square root, quadratic polynomial, cubic polynomial, piecewise-linear function with break in 170):

fit_disp <- list()
fit_disp[["line"]] <- lm(mpg ~ disp, data = mtcars)
fit_disp[["sqrt"]] <- lm(mpg ~ sqrt(disp), data = mtcars)
fit_disp[["log2"]] <- lm(mpg ~ log2(disp), data = mtcars)
fit_disp[["quad"]] <- lm(mpg ~ disp + disp^2, data = mtcars)                   # wrong!!!
fit_disp[["quad"]] <- lm(mpg ~ disp + I(disp^2), data = mtcars)                # this is correct!
fit_disp[["cube"]] <- lm(mpg ~ disp + I(disp^2) + I(disp^3), data = mtcars)
fit_disp[["hoc1"]] <- lm(mpg ~ pmin(disp-170, 0) + pmax(170, disp), data = mtcars)
fit_disp[["hoc2"]] <- lm(mpg ~ disp + pmax(170, disp), data = mtcars)
fit_disp[["flat"]] <- lm(mpg ~ pmin(170, disp), data = mtcars)

sum_disp <- lapply(fit_disp, summary) # summary for each model in the list

Notice that the additional power terms of disp have to be wrapped by I(). The reason is that ^2 has different meaning in formula notation (interactions).

Functions min and max return always only one number - minimum or maximum from all given numbers. However, we wish to compute minimum or maximum in vectorized form, always from two numbers. This is done with pmin and pmax.

The models fit_disp_hoc1 and fit_disp_hoc2 are two equivalent parametrizations of the same function. In the first one, beta coefficients (besides intercept) correspond to the slopes in different intervals. \[ f(x) = \left\{ \begin{aligned} a_1 + b_1 x, & \quad \text{for}\; x \in (-\infty, 170], \\ a_2 + b_2 x, & \quad \text{for}\; x \in [170, \infty). \end{aligned} \right. \quad \Longrightarrow \quad f(x) = a_2 + b_1 \min (x-170, 0) + b_2 \max(170, x) \] The second parametrization, the second coefficient is the slope in the first interval \((-\infty, 170]\) and the third coefficient describes the change from this slope to the slope in the other interval \([170, \infty)\). \[ f(x) = \left\{ \begin{aligned} a_1 + b x, & \quad \text{for}\; x \in (-\infty, 170], \\ a_2 + (b + \delta) x, & \quad \text{for}\; x \in [170, \infty). \end{aligned} \right. \quad \Longrightarrow \quad f(x) = a_2 + b x + \delta \max(170, x) \] The intercept is the same in both cases as it corresponds to the intercept on the second interval. Compare:

sum_disp[["hoc1"]]
## 
## Call:
## lm(formula = mpg ~ pmin(disp - 170, 0) + pmax(170, disp), data = mtcars)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -3.595 -1.680  0.067  1.115  4.866 
## 
## Coefficients:
##                     Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         22.17664    1.66970   13.28  7.4e-14 ***
## pmin(disp - 170, 0) -0.12180    0.01569   -7.77  1.5e-08 ***
## pmax(170, disp)     -0.01961    0.00535   -3.67  0.00098 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.36 on 29 degrees of freedom
## Multiple R-squared:  0.856,  Adjusted R-squared:  0.846 
## F-statistic: 86.2 on 2 and 29 DF,  p-value: 6.26e-13
sum_disp[["hoc2"]]
## 
## Call:
## lm(formula = mpg ~ disp + pmax(170, disp), data = mtcars)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -3.595 -1.680  0.067  1.115  4.866 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      22.1766     1.6697   13.28  7.4e-14 ***
## disp             -0.1218     0.0157   -7.77  1.5e-08 ***
## pmax(170, disp)   0.1022     0.0194    5.26  1.2e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.36 on 29 degrees of freedom
## Multiple R-squared:  0.856,  Adjusted R-squared:  0.846 
## F-statistic: 86.2 on 2 and 29 DF,  p-value: 6.26e-13

See? Intercept rows are both \(22.17664\). Next, \(-0.1218 + 0.10219 = -0.019607\)

The last model fit_disp_flat has some slope in the first interval, but after 170 there is no trend only constant.

In order to plot the fitted curves we define the functions:

fun <- list()
fun[["line"]] <- function(beta, x){beta[1] + beta[2] * x}
fun[["sqrt"]] <- function(beta, x){beta[1] + beta[2] * sqrt(x)}
fun[["log2"]] <- function(beta, x){beta[1] + beta[2] * log2(x)}
fun[["quad"]] <- function(beta, x){beta[1] + beta[2] * x + beta[3] * x^2}
fun[["cube"]] <- function(beta, x){beta[1] + beta[2] * x + beta[3] * x^2 + beta[4] * x^3}
fun[["hoc1"]] <- function(beta, x){beta[1] + beta[2] * pmin(x-170, 0) + beta[3] * pmax(170, x)}
fun[["hoc2"]] <- function(beta, x){beta[1] + beta[2] * x + beta[3] * pmax(170, x)}
fun[["flat"]] <- function(beta, x){beta[1] + beta[2] * pmin(170, x)}

Now we plot all the fitted curves into one plot:

xgrid <- seq(min(mtcars$disp), max(mtcars$disp), length.out = 201)
COL <- c("blue", "purple", "orchid", "green", "darkgreen", "orange", "red", "peru")
names(COL) <- names(fit_disp)
nice_labels <- c("line", "square root", expression(log[2]), 
                 "quadratic", "cubic", 
                 "hockey 1", "hockey 2", "flat hockey")

par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, 
     xlab = "Displacement [cubic inches]", ylab = "Miles per gallon", 
     pch = 22, cex = 0.8, bg = "lightblue")
abline(v = 170, col = "grey", lty = 3)
# now add the estimated curves 
for(curve in names(fit_disp)){
  lines(xgrid, fun[[curve]](coef(fit_disp[[curve]]), xgrid), 
        col = COL[curve], lwd = 2, lty = ifelse(curve == "hoc2", 2, 1))
}
legend("topright", legend = nice_labels, bty = "n",
       col = COL, lty = c(1,1,1,1,1,2,1), lwd = 2)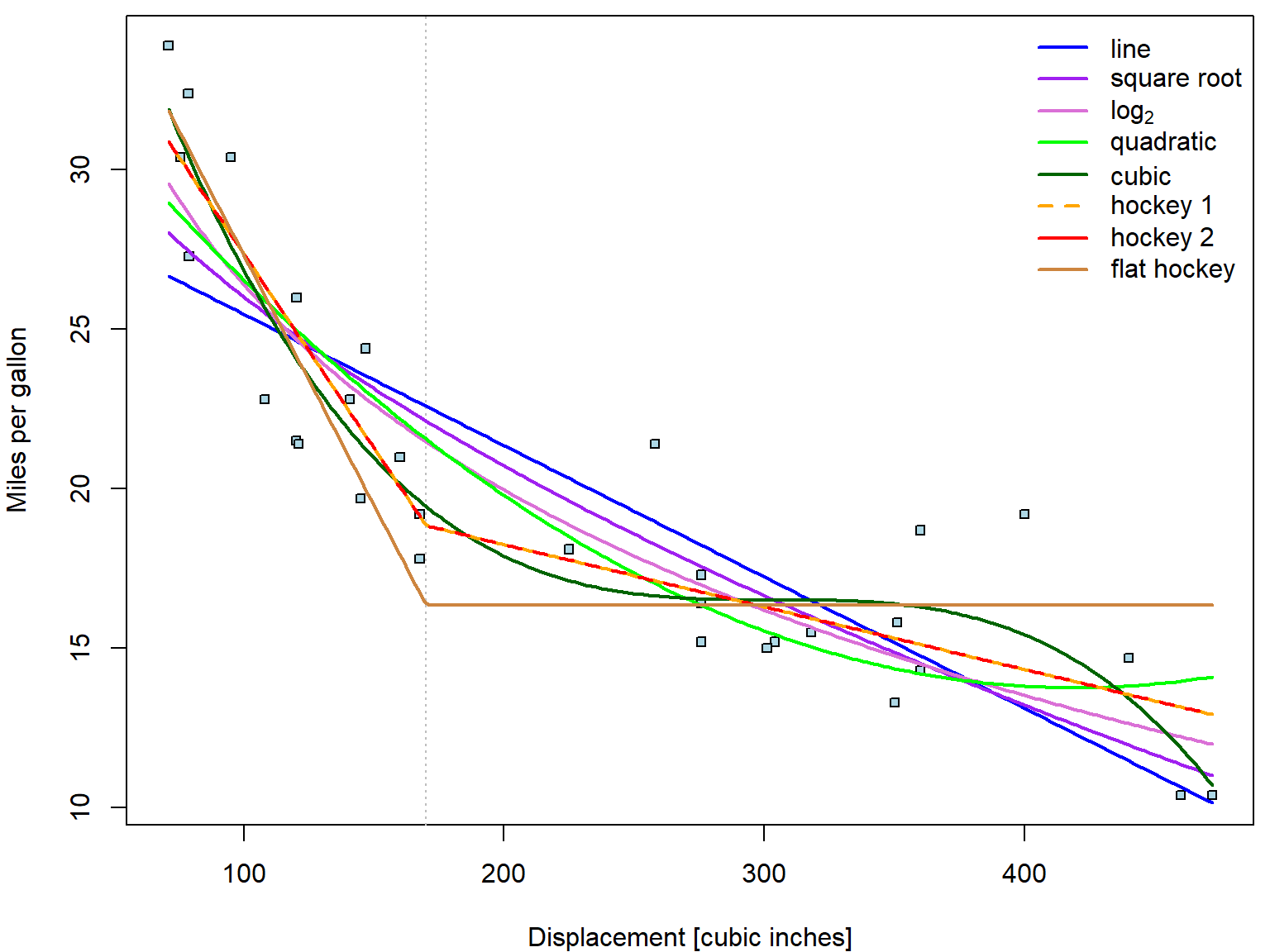

You actually do not have to define the functions on your own. There is always an option to use predict function to estimate the fitted value fit given grid of newdata covariates.

pred_disp <- lapply(fit_disp, predict, newdata = data.frame(disp = xgrid))

The predict function will work this way as long as disp is transformed directly within the model formula. If you would define disp2 = disp^2, then your newdata need to contain disp2 as well. See? The results are the same:

par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
plot(mpg ~ disp, data = mtcars, 
     xlab = "Displacement [cubic inches]", ylab = "Miles per gallon", 
     pch = 22, cex = 0.8, bg = "lightblue")
abline(v = 170, col = "grey", lty = 3)
# now add the estimated curves 
for(curve in names(fit_disp)){
  lines(xgrid, pred_disp[[curve]], 
        col = COL[curve], lwd = 2, lty = ifelse(curve == "hoc2", 2, 1))
}
legend("topright", legend = nice_labels, bty = "n",
       col = COL, lty = c(1,1,1,1,1,2,1), lwd = 2)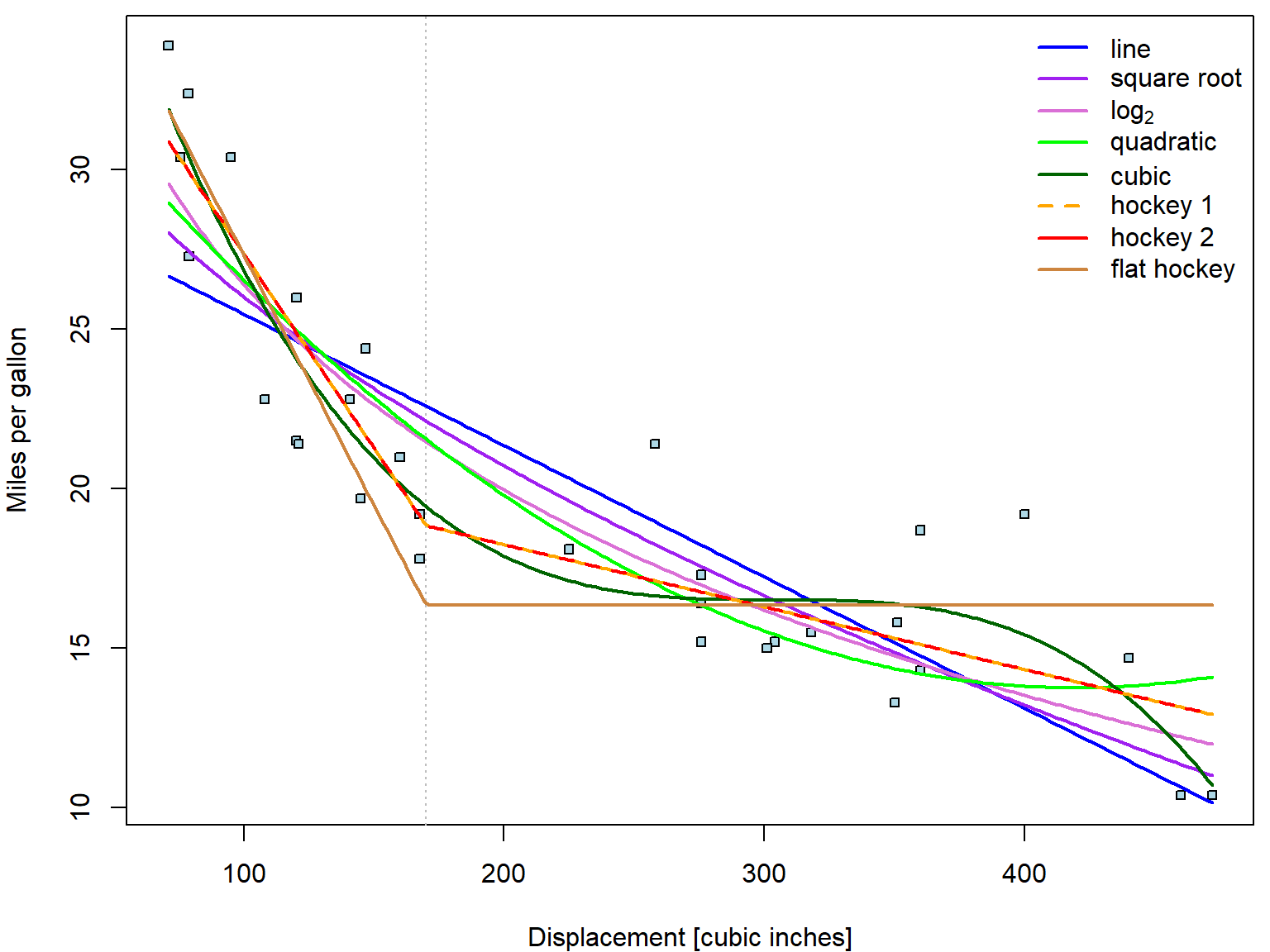

How do we choose suitable transformation?

table <- data.frame(R2 = unlist(lapply(sum_disp, function(s){s$r.squared})),
                    adjR2 = unlist(lapply(sum_disp, function(s){s$adj.r.squared})),
                    Fpval = unlist(lapply(sum_disp, function(s){
                      pf(s$fstatistic["value"], df1 = s$fstatistic["numdf"],
                         df2 = s$fstatistic["dendf"], lower.tail = FALSE
                         )})),
                    AIC = unlist(lapply(fit_disp, AIC)))

library(knitr)
kable(table, digits = 15)
R2 adjR2 Fpval AIC
line 0.7183 0.7090 9.380e-10 170.2
sqrt 0.7756 0.7681 2.993e-11 162.9
log2 0.8229 0.8169 8.400e-13 155.4
quad 0.7927 0.7784 1.229e-10 162.4
cube 0.8771 0.8639 7.350e-13 147.7
hoc1 0.8560 0.8461 6.260e-13 150.7
hoc2 0.8560 0.8461 6.260e-13 150.7
flat 0.7892 0.7822 1.162e-11 160.9 
par(mfrow = c(2,4), mar = c(4,4,2,0.5))
for(curve in names(fit_disp)){
  plot(fit_disp[[curve]], which = 1)
  legend("topright", legend = curve)
}

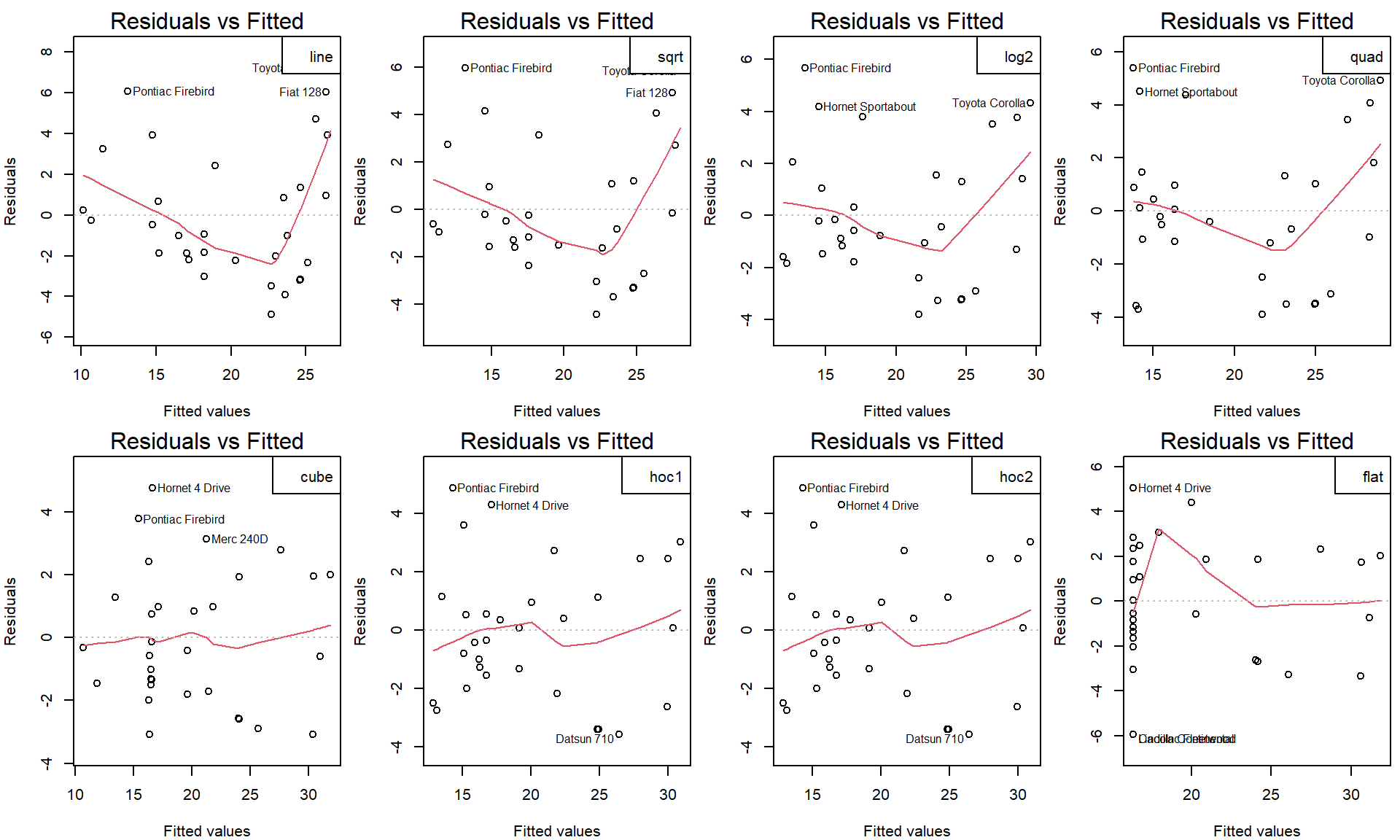
Individual work