Je dána krychle \(ABCDEFGH\), kde \(|AB|=4 \mbox{ cm}\), a bod \(M\), který je průsečíkem úhlopříček stěny \(ABF\). Určete vzdálenost bodů \(C\), \(M\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení

Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4 \mbox{ cm}\). Dále jsou dány body \(K\), \(L\). Bod \(K\) náleží hraně \(DV\) a platí \(|KV|=\frac{1}{4}|DV|.\) Bod \(L\) je středem hrany \(BV\). Určete vzdálenost bodů \(K\), \(L\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Ze zadání víme, že: \(|S_{DV}K|=|KV|=\frac{1}{4}|DV|\) K určení délky \(|S_{DV}K|\) tedy využijeme trojúhelník \(DSV\): \[|S_{DV}K|=\frac{1}{4}\sqrt{\Bigl(2\sqrt{2}\Bigr)^2+4^2}=\frac{1}{4}\sqrt{24} = \frac{\sqrt{6}}{2}\] Abychom mohli určit délku úsečky \(KL\) pomocí kosinové věty, potřebujeme zjistit velikost úhlu \(\varphi=|\angle SDV|=|\angle S'S_{DV}V|\) v trojúhelníku \(DSV\): \[\tan\varphi=\frac{|VS|}{|DS|}=\frac{4}{2\sqrt{2}}=\sqrt{2}\Rightarrow\varphi\doteq 54^\circ 44'\] Nyní již pomocí kosinové věty v \(\triangle S_{DV}LK\) určíme délku \(KL\): \[|KL|^2=|S_{DV}K|^2+|S_{DV}L|^2-2|S_{DV}K||S_{DV}L|\cos\varphi\] \[|KL|^2=\Bigl(\frac{\sqrt{6}}{2}\Bigr)^2+\Bigl(2\sqrt{2}\Bigr)^2-2\frac{\sqrt{6}}{2}2\sqrt{2}\cos(54^\circ 44')\] \[|KL|\doteq 2,35 \mbox{ cm}\]
Syntetické konstrukční řešení
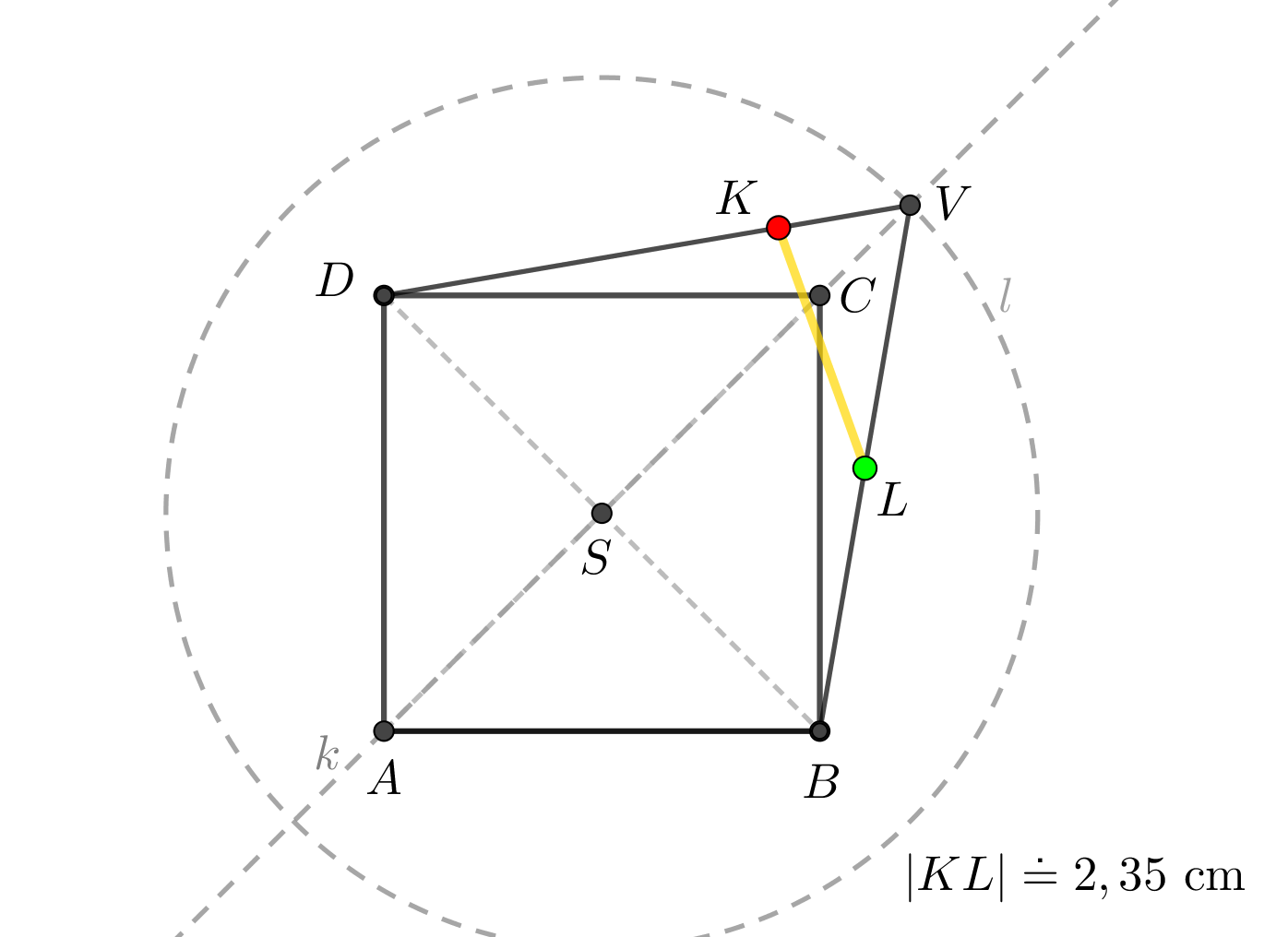
Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 6\mbox{ cm}\). Určete vzdálenost bodů \(S_{AV}\), \(C\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Nyní za jednotlivé souřadnice bodů \(S_{AV}\) a \(C\) dosadíme hodnoty dle vhodného umístění do kartézské soustavy souřadnic: \[|S_{AV}C|=\sqrt{(4-1)^2+(4-1)^2+(0-3)^2}=\sqrt{3^2+3^2+(-3)^2}=\sqrt{27}=3\sqrt{3}\doteq 5,2\mbox{ cm}\]
Syntetické početní řešení

Syntetické konstrukční řešení

Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost bodu \(S_{FH}\) od roviny \(ABC\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
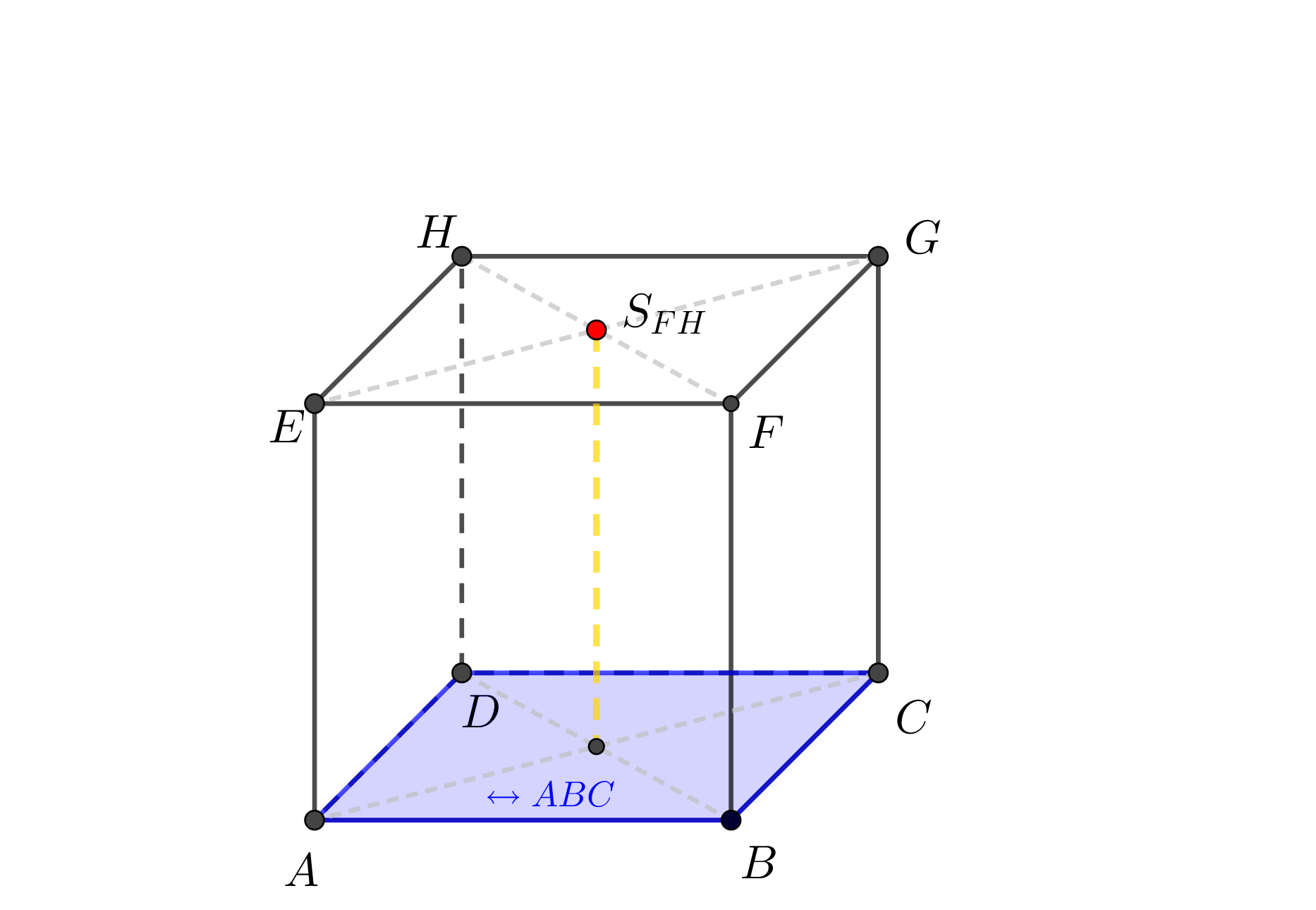
Syntetické konstrukční řešení

Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost bodu \(F\) od roviny \(BGE\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
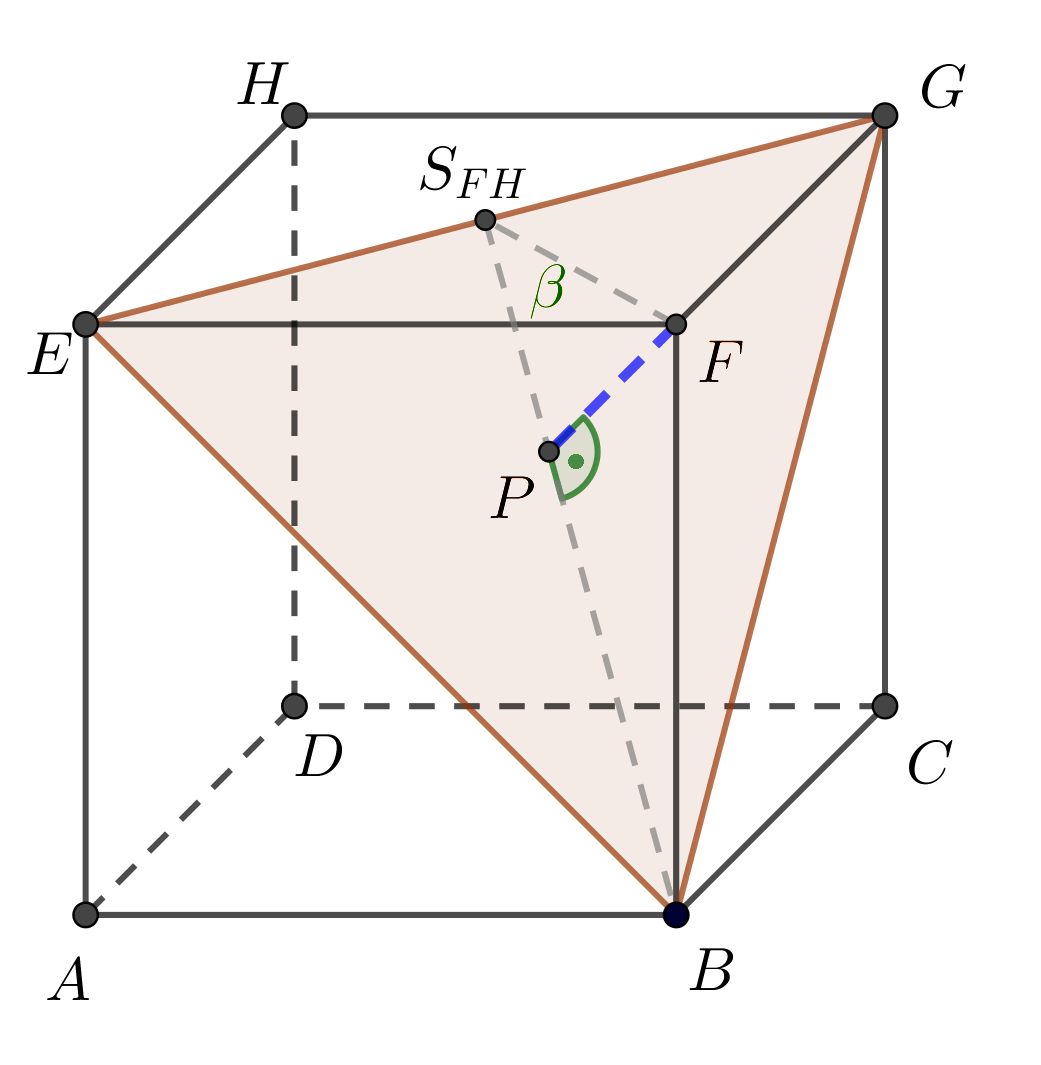
Syntetické konstrukční řešení
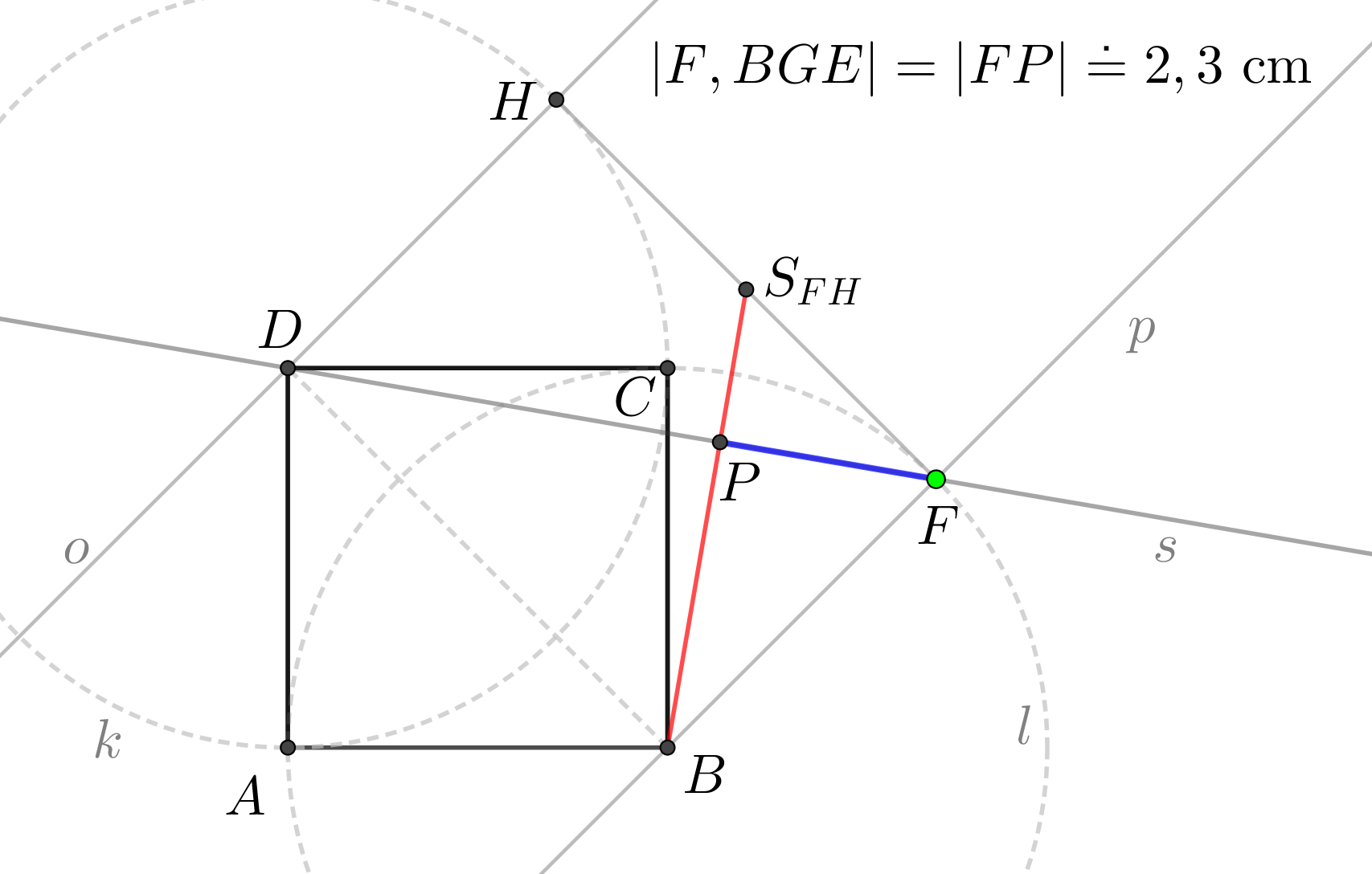
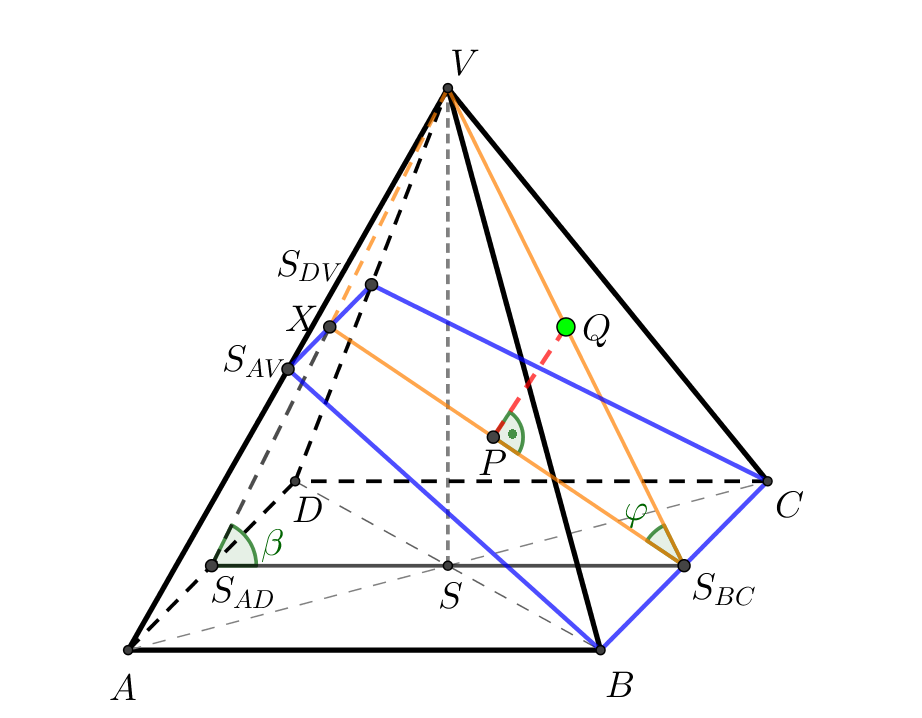
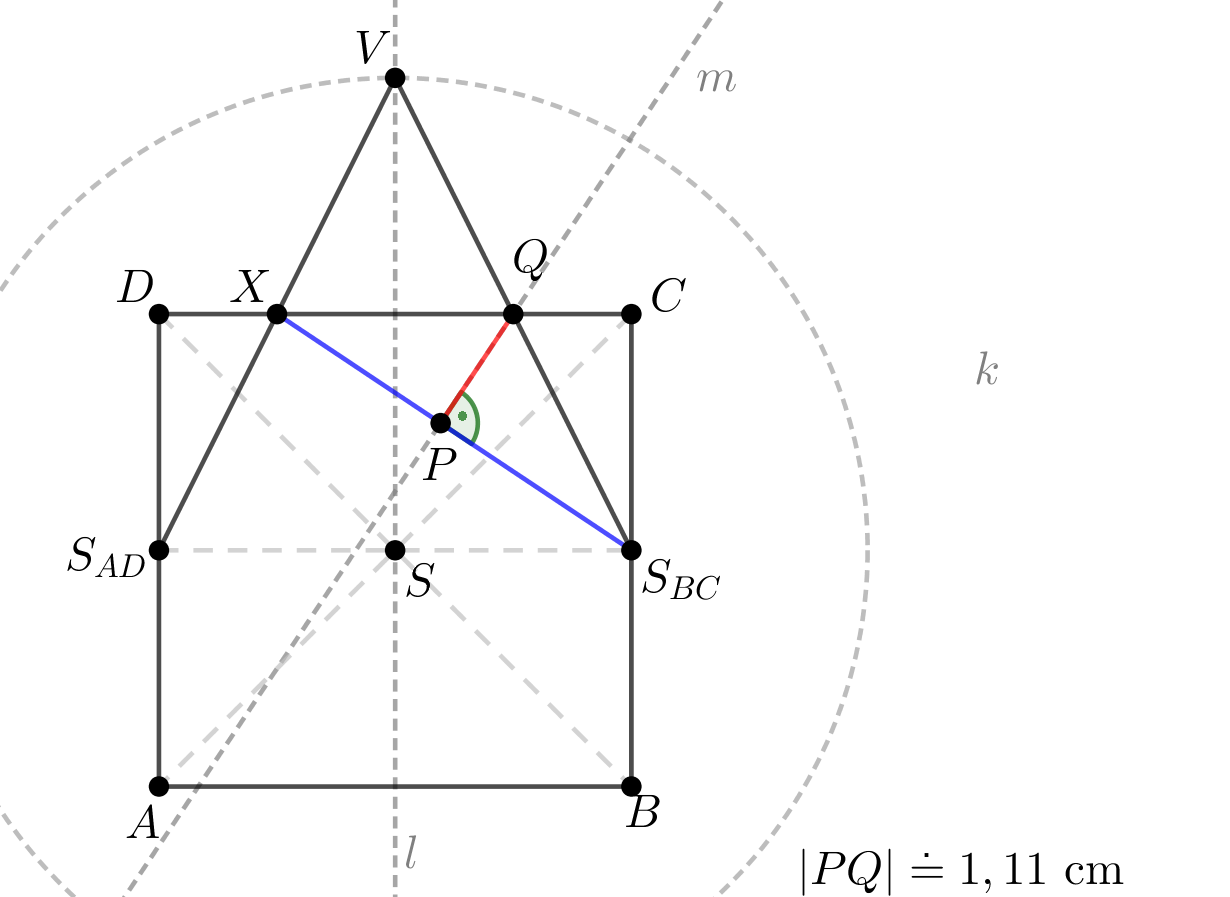
Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4\mbox{ cm}\). Dále je dán bod \(Q\), který je středem úsečky \(S_{BC}V\). Určete vzdálenost bodu \(Q\) od roviny \(BCS_{DV}\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
Syntetické konstrukční řešení
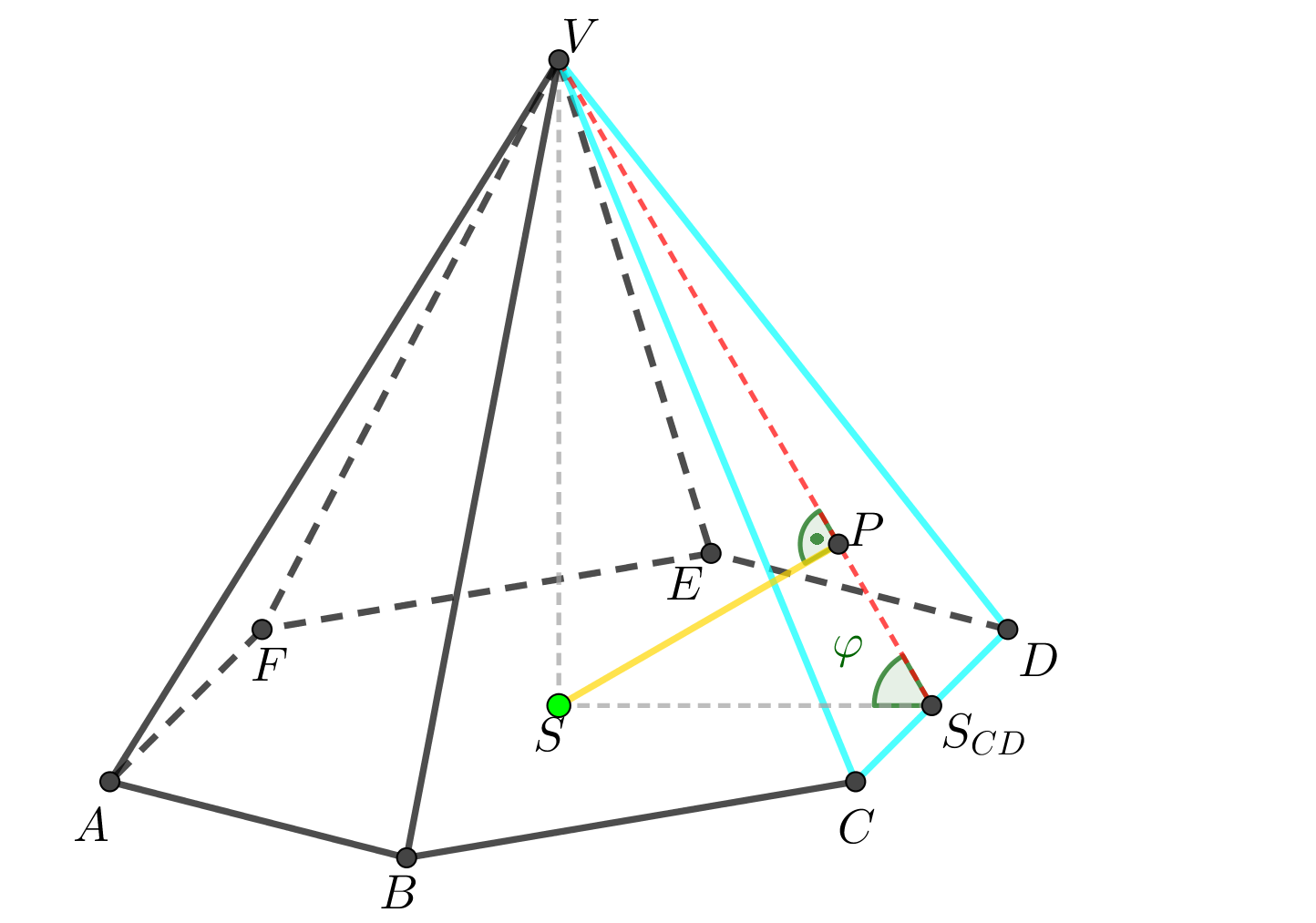
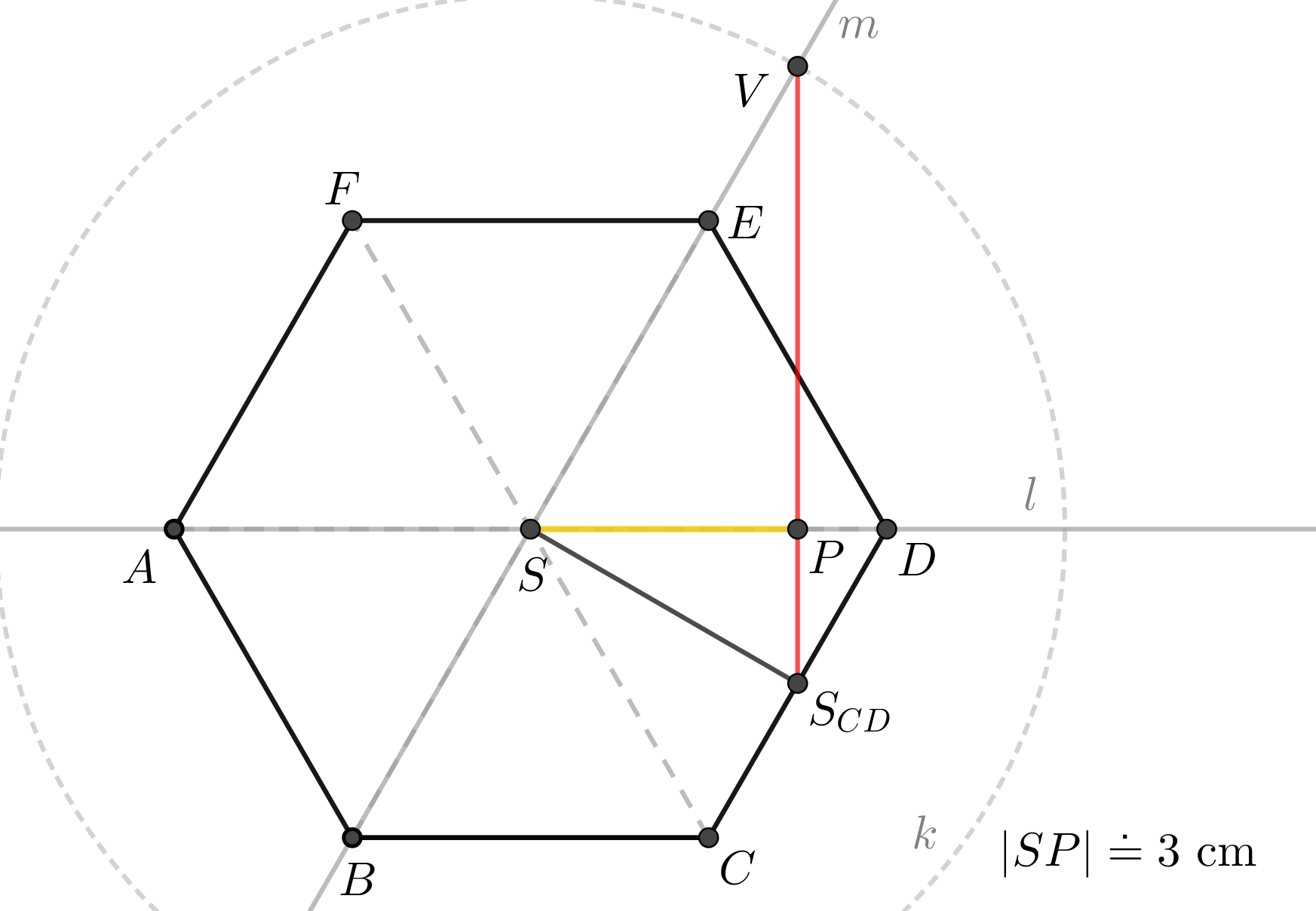
Je dán pravidelný šestiboký jehlan \(ABCDEFV\) s podstavou \(ABCDEF\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 6\mbox{ cm}\). Určete vzdálenost bodu \(S\) od roviny boční stěny jehlanu.
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
Syntetické konstrukční řešení
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost přímky \(S_{DH}F\) od roviny \(AS_{BF}D\).
Znázornění situace
Analytické řešení
Zadanou krychli jsem vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
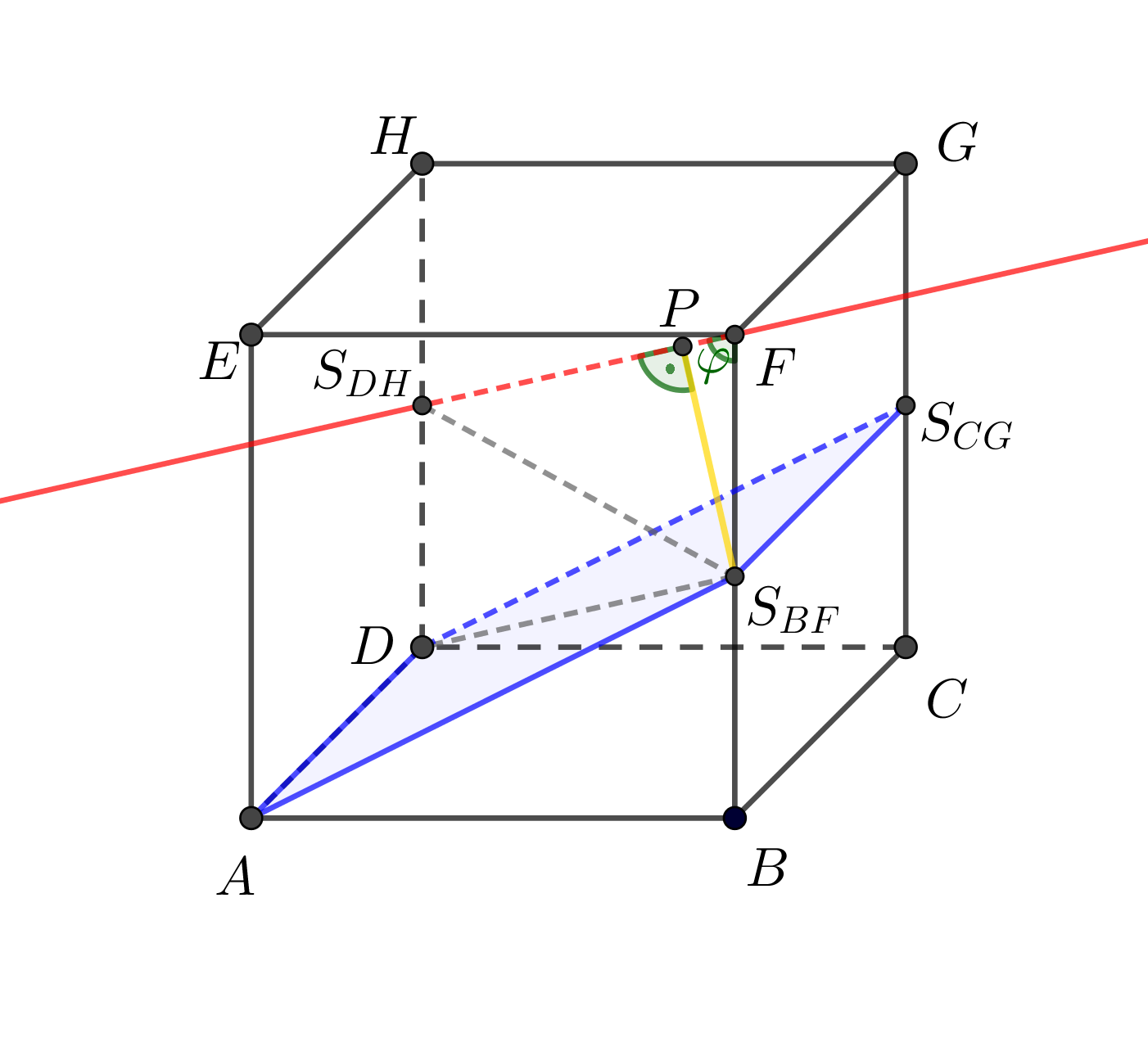
Syntetické konstrukční řešení

Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4\mbox{ cm}\). Určete vzdálenost přímky \(S_{DV}S_{AB}\) od roviny \(BCV\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

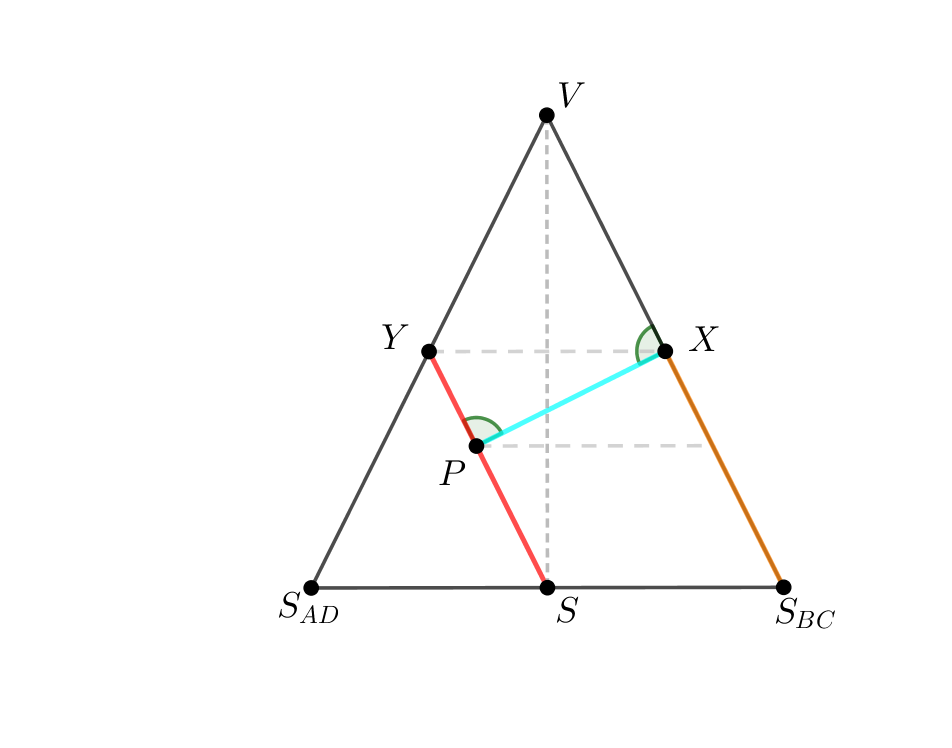
Syntetické konstrukční řešení

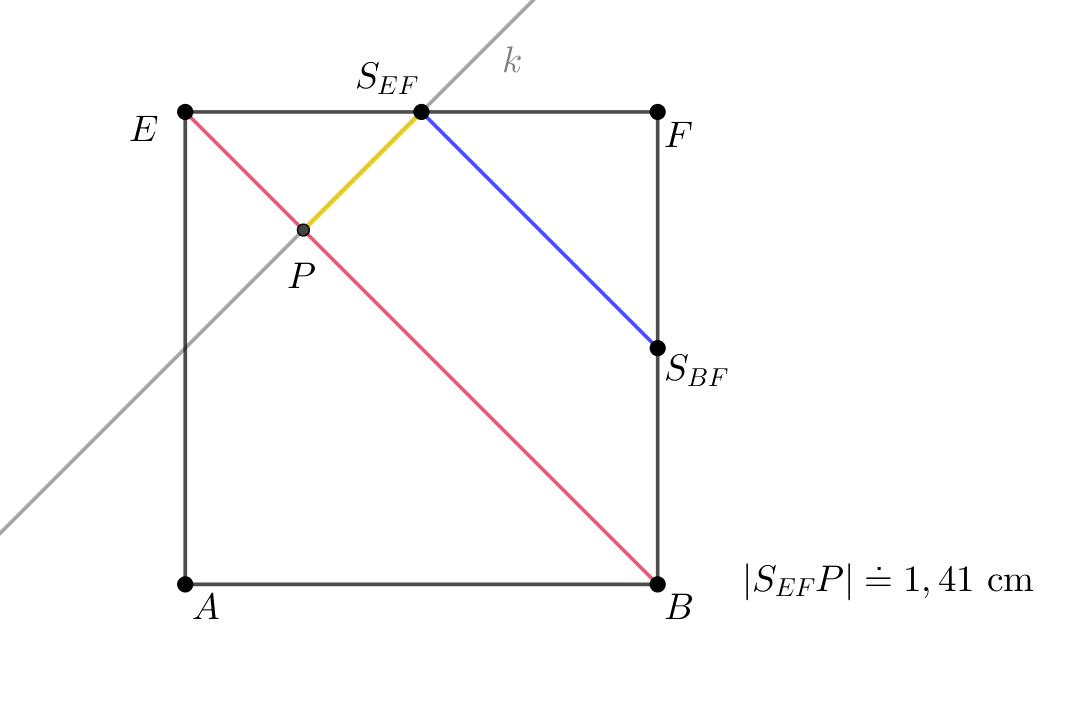
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost rovin \(EBC\) a \(S_{EF}S_{BF}S_{CG}\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
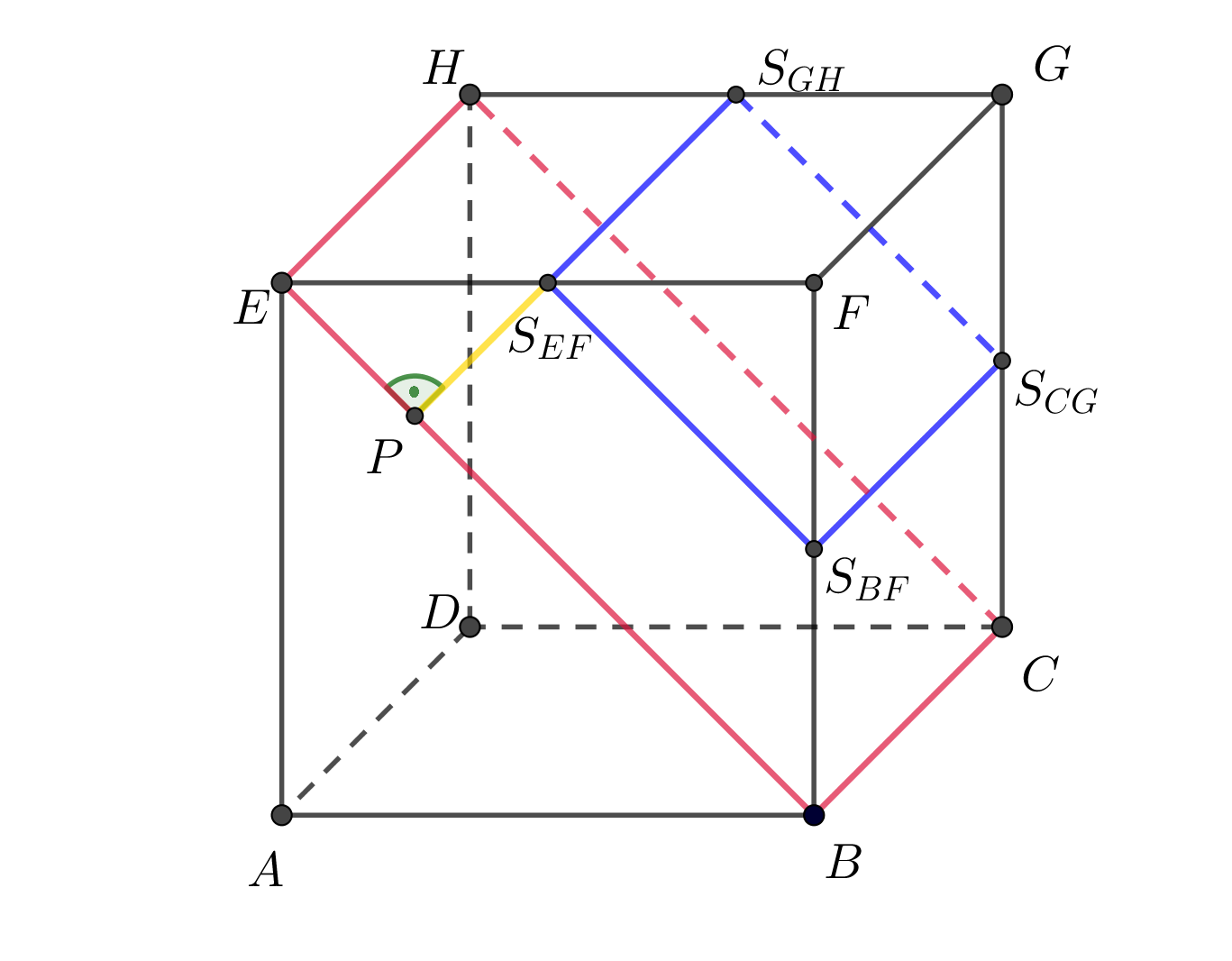
Syntetické konstrukční řešení
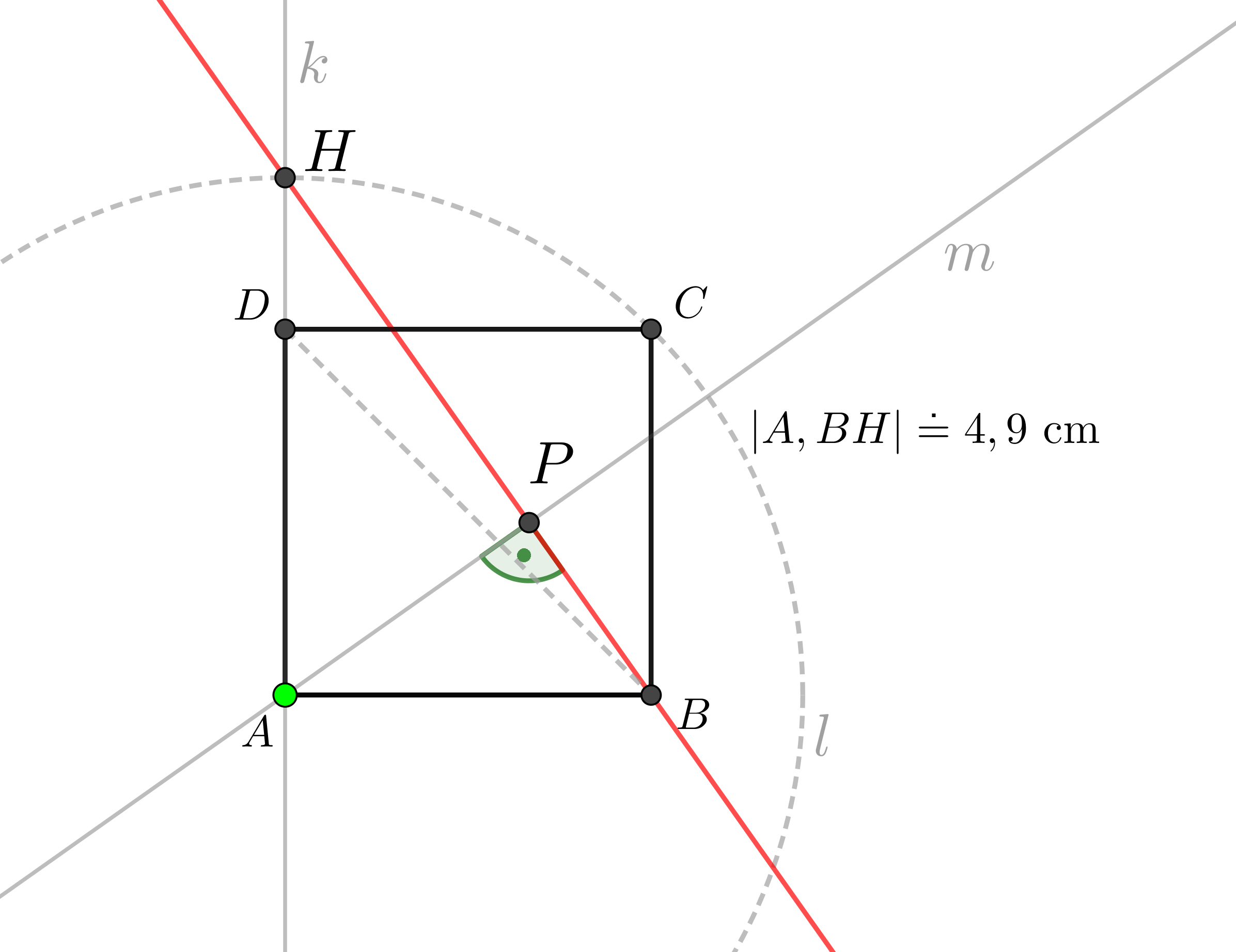
Je dána krychle \(ABCDEFGH\), \(|AB| = 6\mbox{ cm}\). Určete vzdálenost bodu \(A\) od přímky \(BH\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení
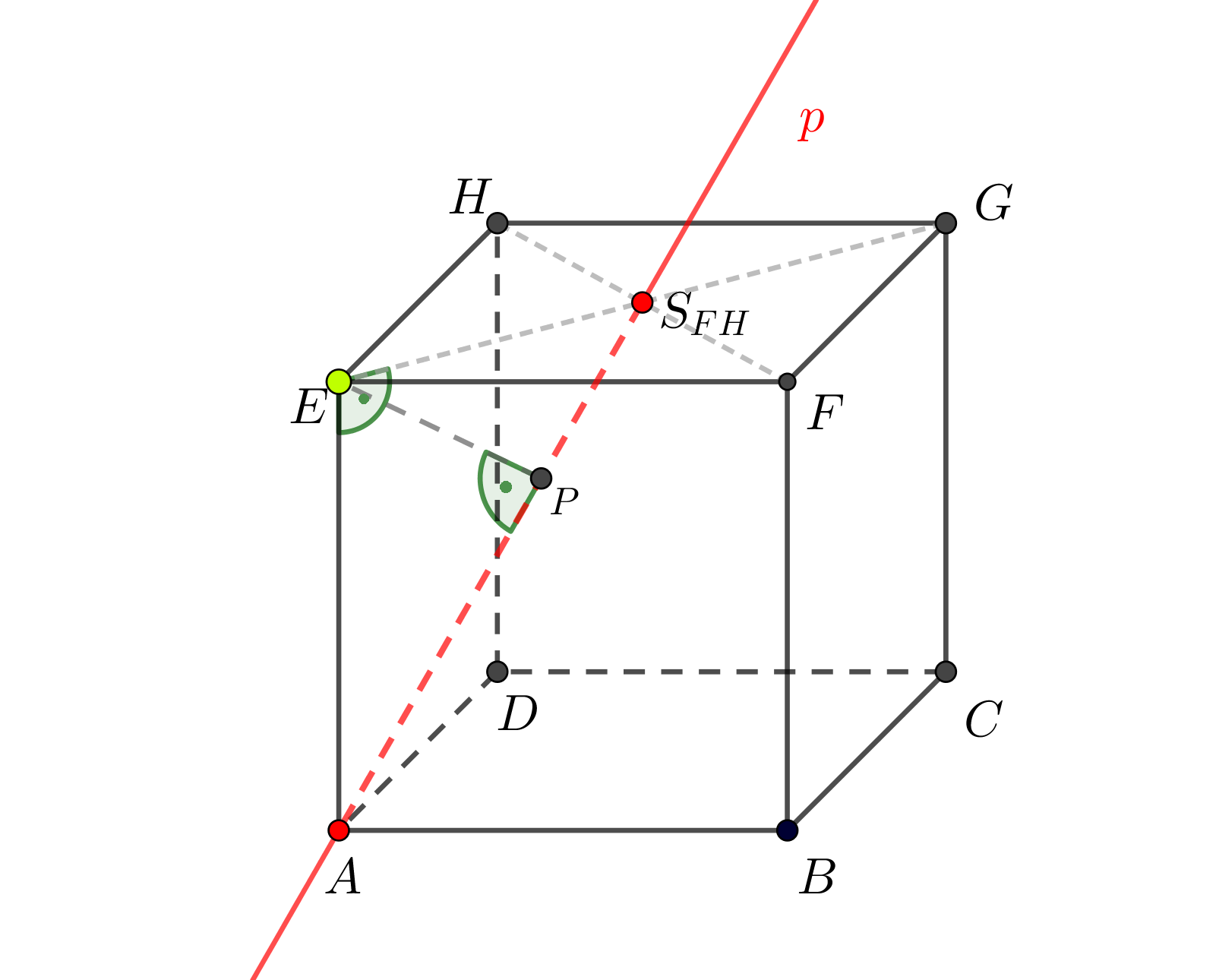
Je dána krychle \(ABCDEFGH\), \(|AB| = 6\mbox{ cm}\). Určete vzdálenost bodu \(E\) od přímky \(AS_{FH}\).
Znázornění situace
Analytické řešení
Zadanou krychli jsem vhodně umístili do soustavy souřadnic:
\[|EP|=\frac{S}{|AS_{FH}|}=\frac{18\sqrt{2}}{\sqrt{3^2+3^2+6^2}}=\frac{18\sqrt{2}}{\sqrt{54}}=\frac{18\sqrt{2}}{3\sqrt{6}}=\frac{6}{\sqrt{3}}=2\sqrt{3}\doteq 3,46\mbox{ cm}\]
Syntetické početní řešení
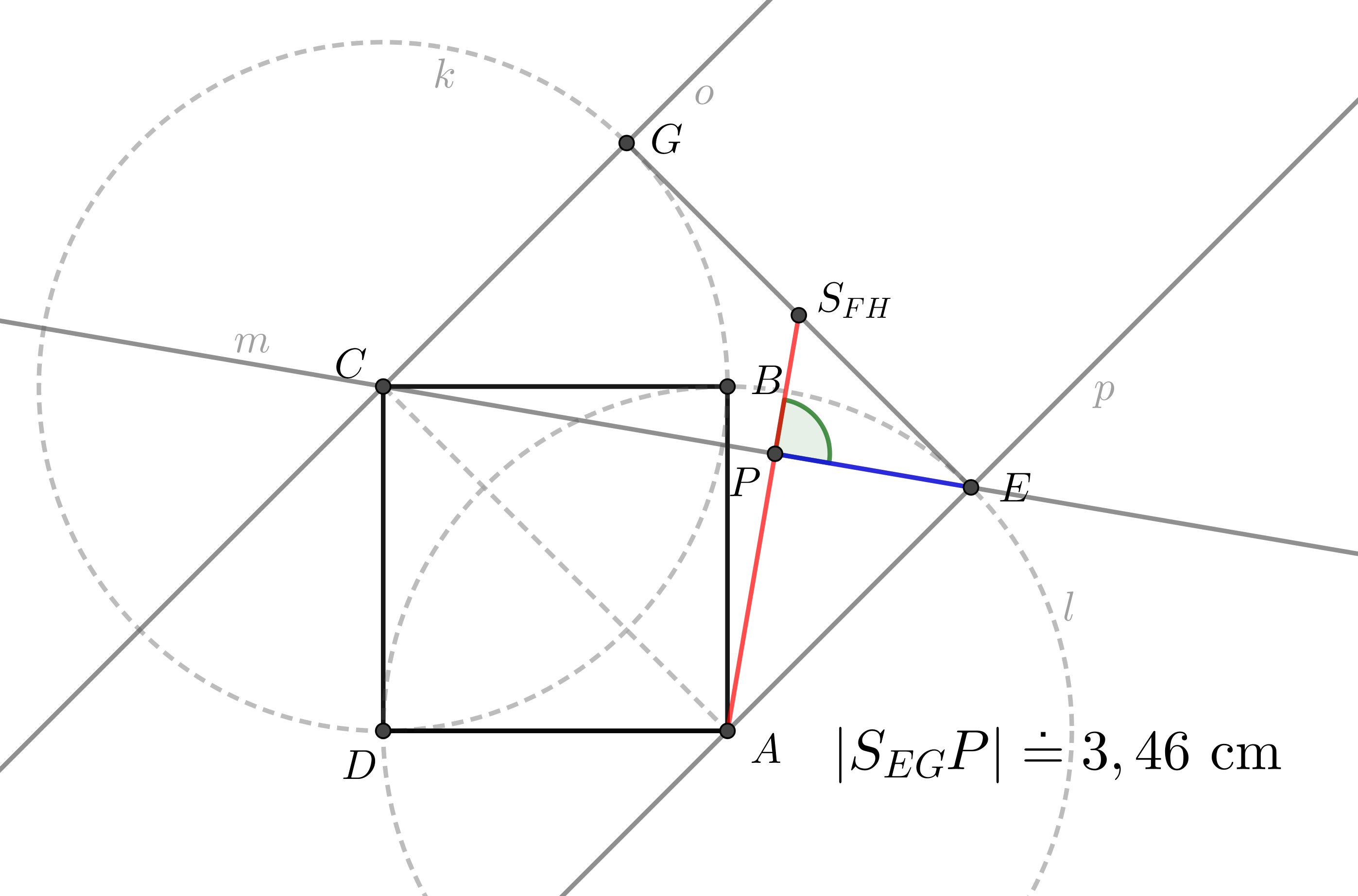
Syntetické konstrukční řešení
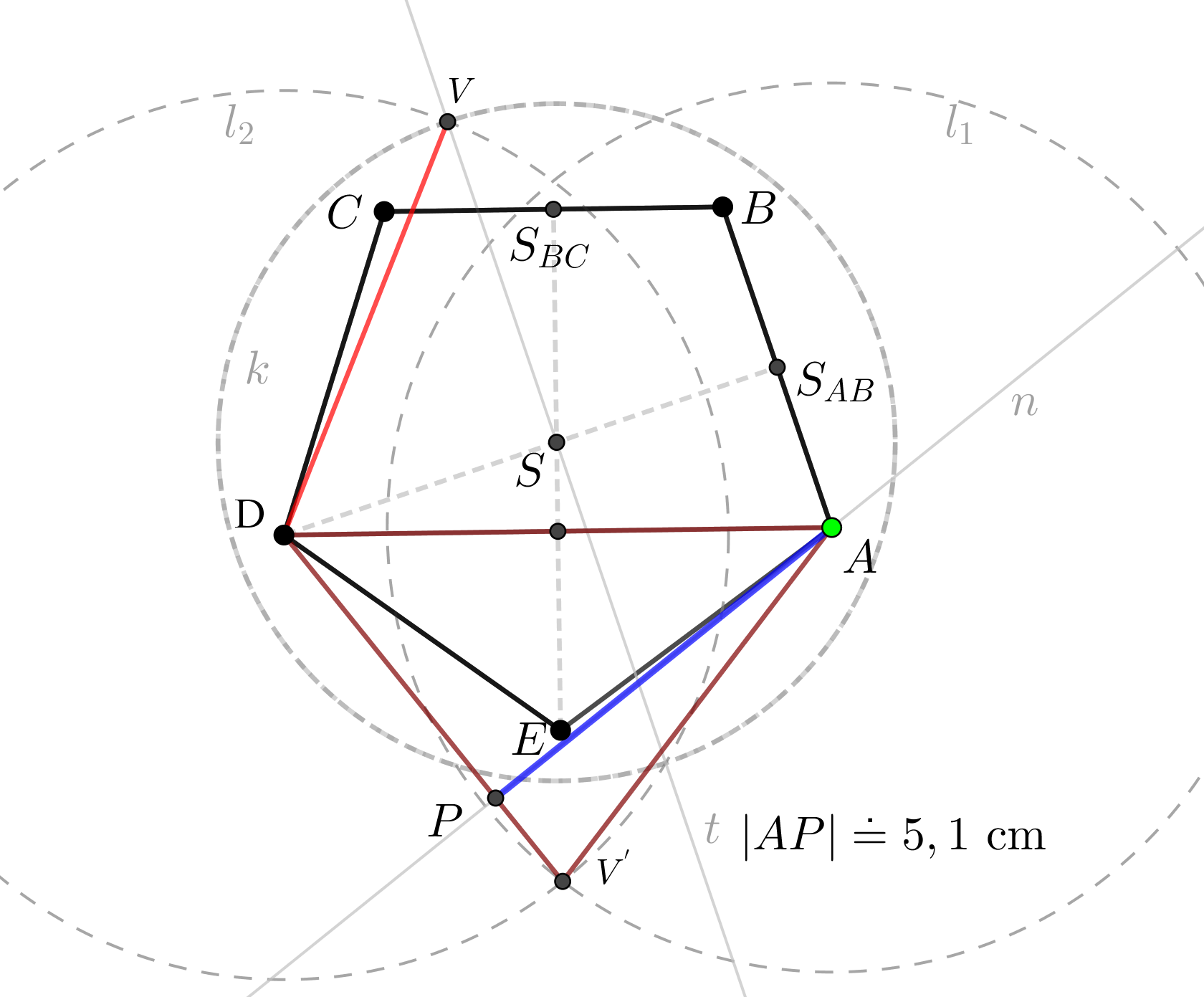
Je dán pravidelný pětiboký jehlan \(ABCDEV\) s podstavou \(ABCDE\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4\mbox{ cm}\). Určete vzdálenost bodu \(A\) od přímky \(DV\).
Znázornění situace
Analytické řešení
Zadaný pětiboký jehlan jsme vhodně umístili do soustavy souřadnic:
Souřadnice bodů \(A\), \(B\) jsme odvodili z trojúhelníku \(ABS\), jehož strana \(AB\) má délku \(4 \mbox{ cm}\) a úhel při vrcholu \(S\) má velikost \(72^\circ\). Obdobným způsobem jsme získali i souřadnice bodu \(D\). Zde jsme vycházeli z trojúhelníku \(DCS\). Souřadnice jsou zaokrouhleny na dvě desetinná místa.
Syntetické početní řešení

Syntetické konstrukční řešení
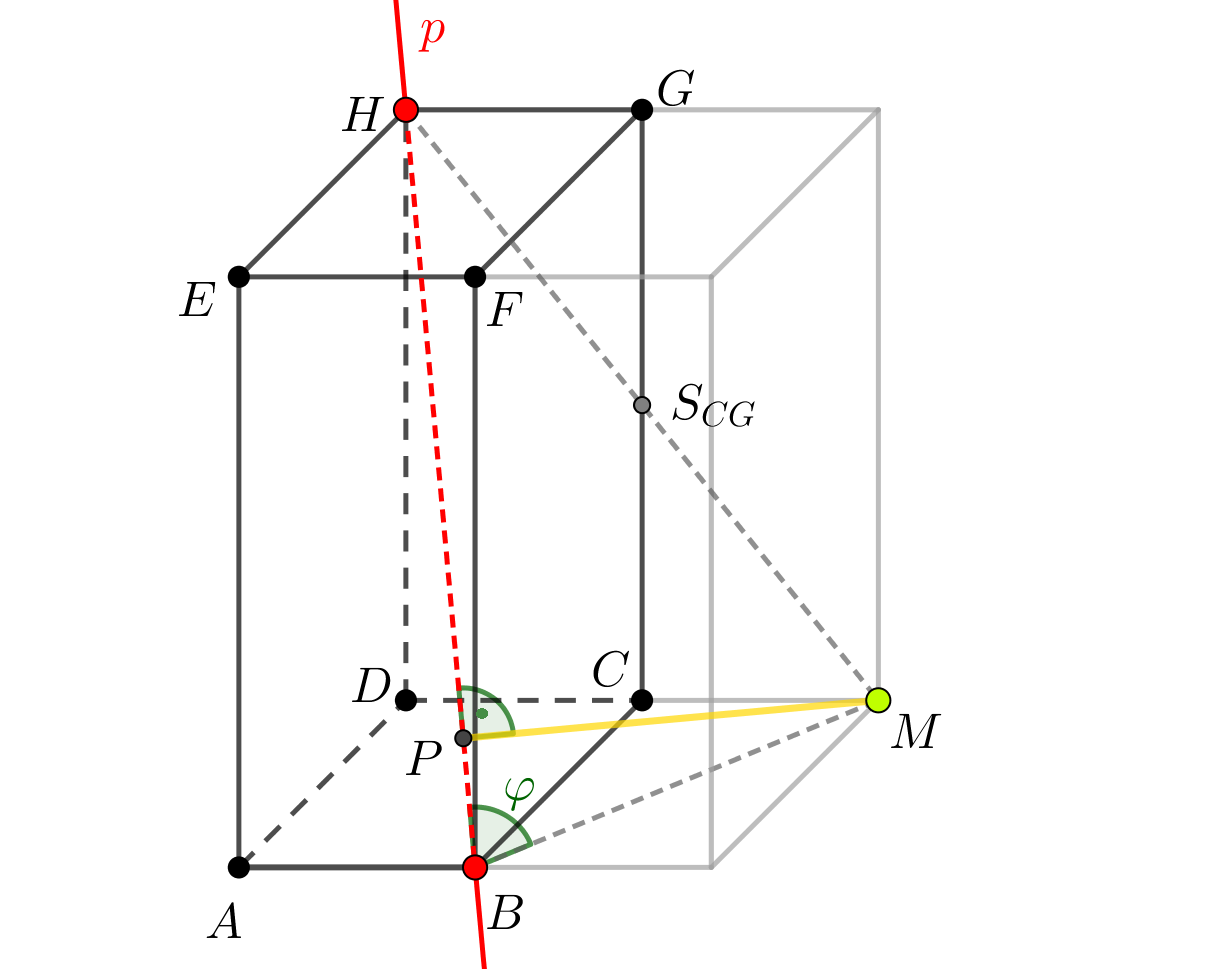
Je dán kvádr \(ABCDEFGH\), \(|AB| = 2\mbox{ cm}\), \(|BC| = 4\mbox{ cm}\), \(|BF| = 5\mbox{ cm}\). Dále je dán bod \(M\) takový, že bod \(C\) je středem úsečky \(DM\). Určete vzdálenost bodu \(M\) od přímky \(BH\).
Znázornění situace
Analytické řešení
Zadanou krychli jsem vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
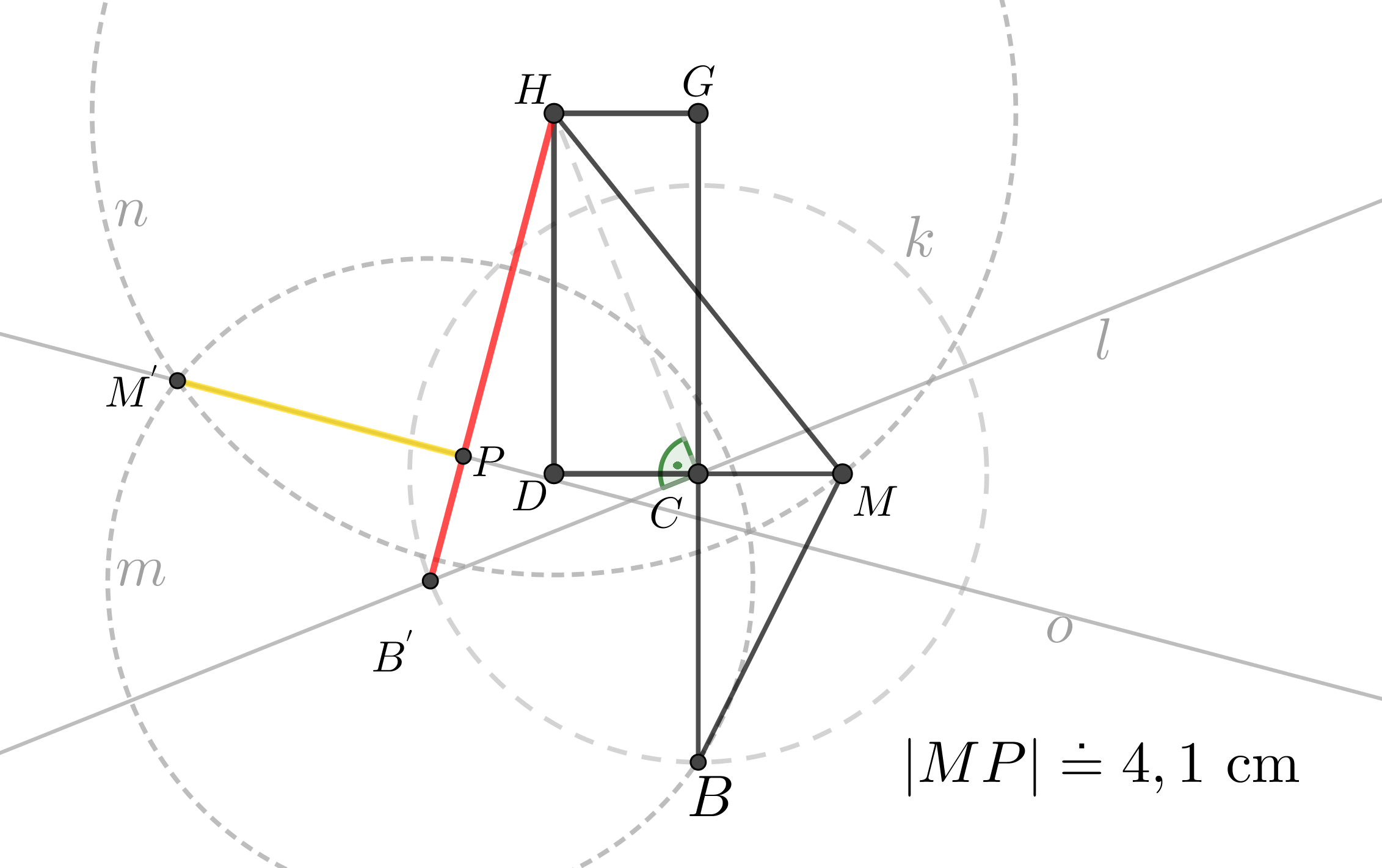
Syntetické konstrukční řešení
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost přímky \(EG\) od přímky \(S_{AB}S_{BC}\).
Znázornění situace
Analytické řešení
Zadanou krychli jsem vhodně umístili do soustavy souřadnic:
\[|PS_{AB}|=\frac{S}{|EG|}=\frac{24}{\sqrt{4^2+4^2+0^2}}=\frac{24}{\sqrt{32}}=\frac{24}{4\sqrt{2}}=\frac{6}{\sqrt{2}}=3\sqrt{2}\doteq 4,24\mbox{ cm}\]
Syntetické početní řešení

Syntetické konstrukční řešení

Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost přímky \(EG\) od přímky \(DF\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení

Je dán pravidelný čtyřstěn \(ABCD\), \(|AB|=4\mbox{ cm}\). Určete vzdálenost hran \(AB\) a \(DC\).
Znázornění situace
Analytické řešení
Zadaný čtyřstěn jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení

