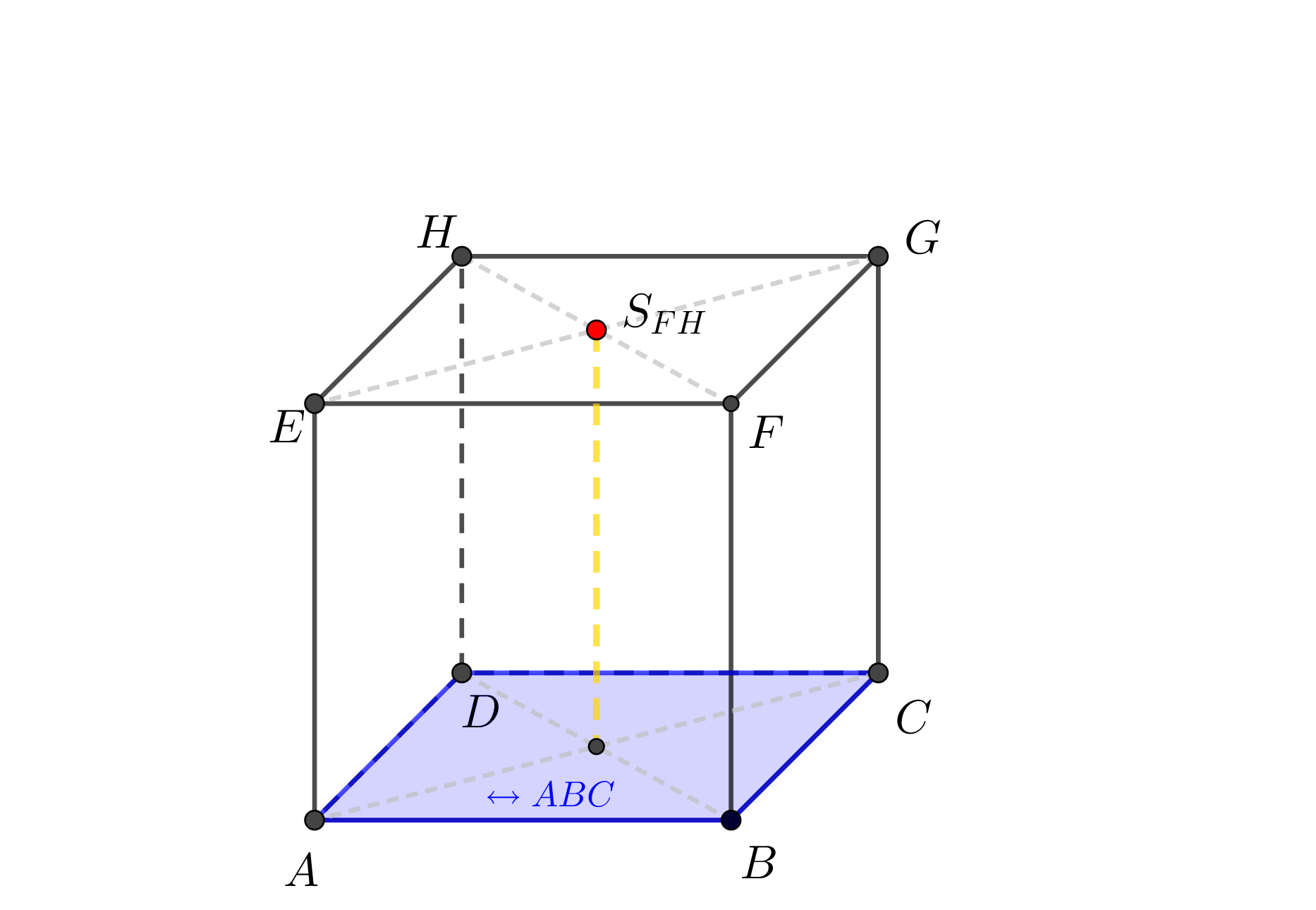
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost bodu \(S_{FH}\) od roviny \(ABC\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
Syntetické konstrukční řešení

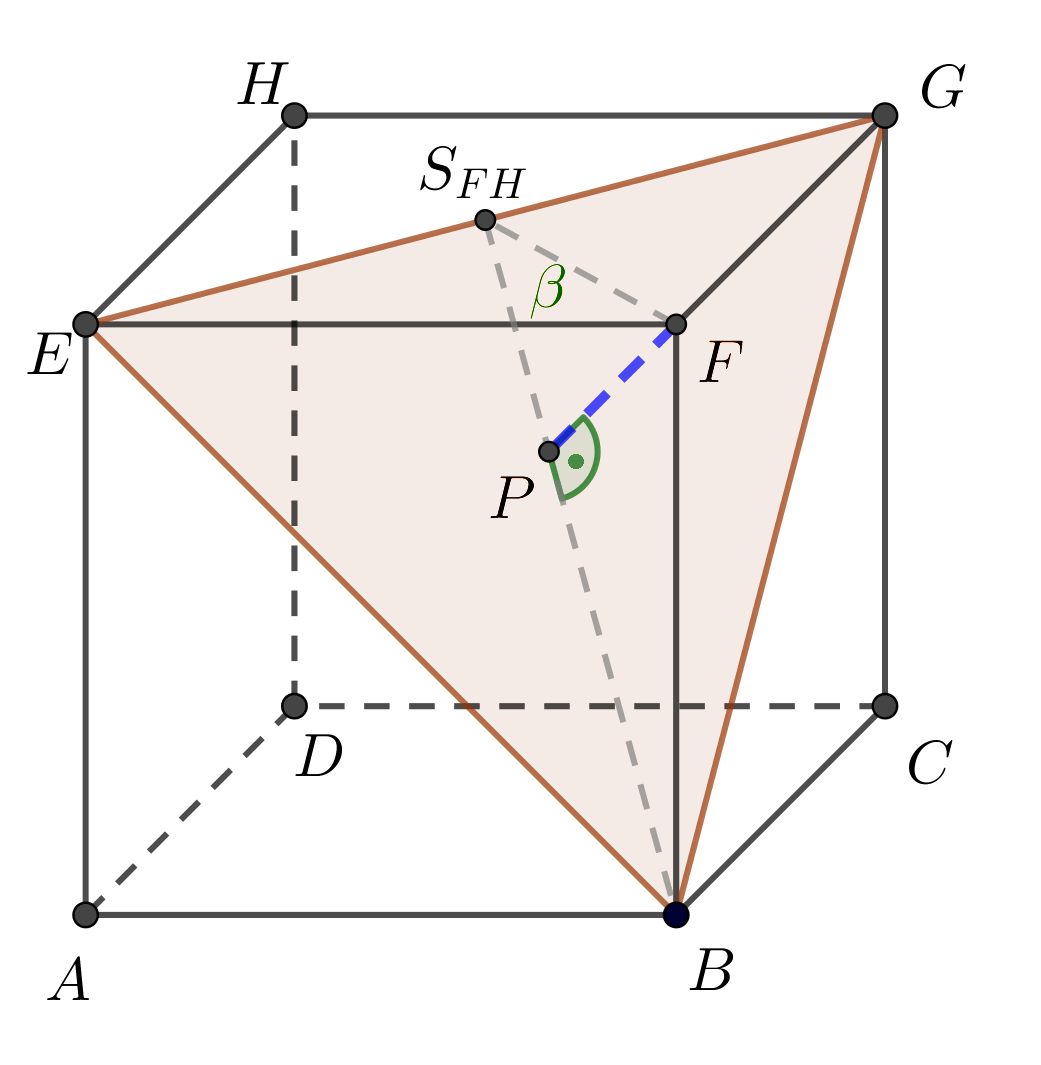
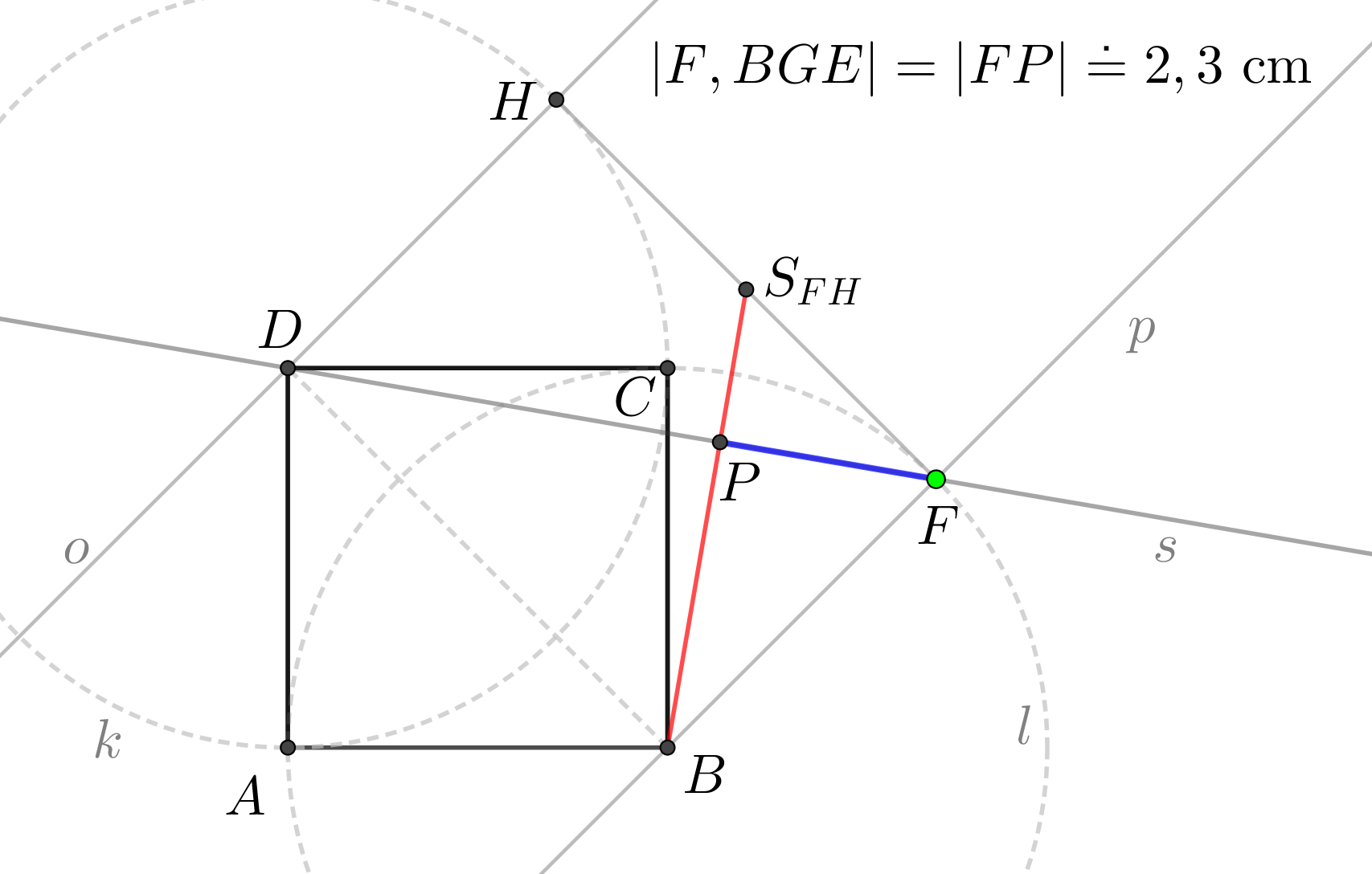
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost bodu \(F\) od roviny \(BGE\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
Syntetické konstrukční řešení
Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4\mbox{ cm}\). Dále je dán bod \(Q\), který je středem úsečky \(S_{BC}V\). Určete vzdálenost bodu \(Q\) od roviny \(BCS_{DV}\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
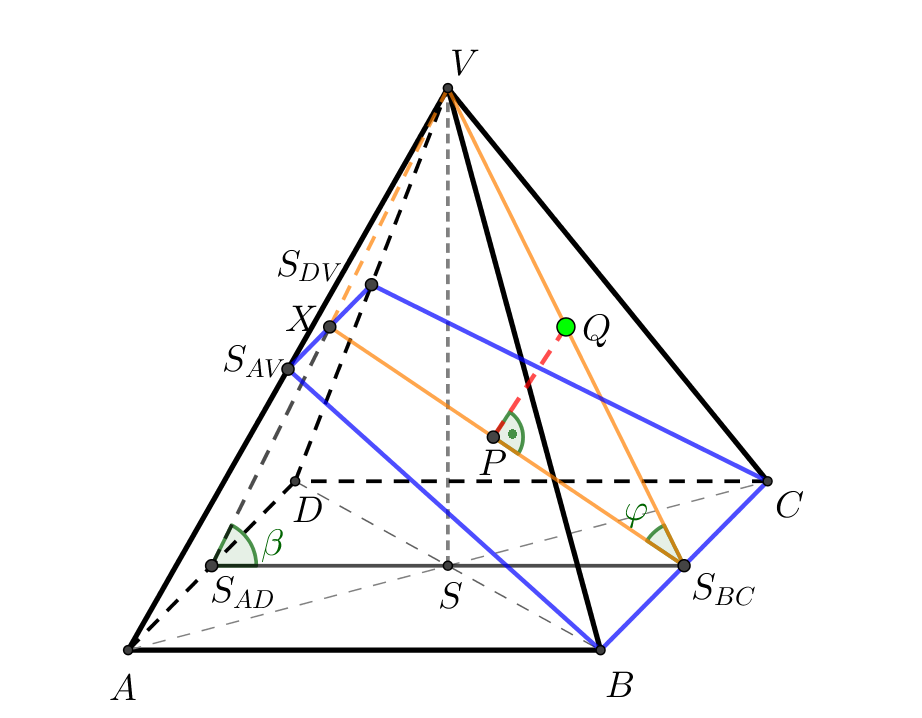
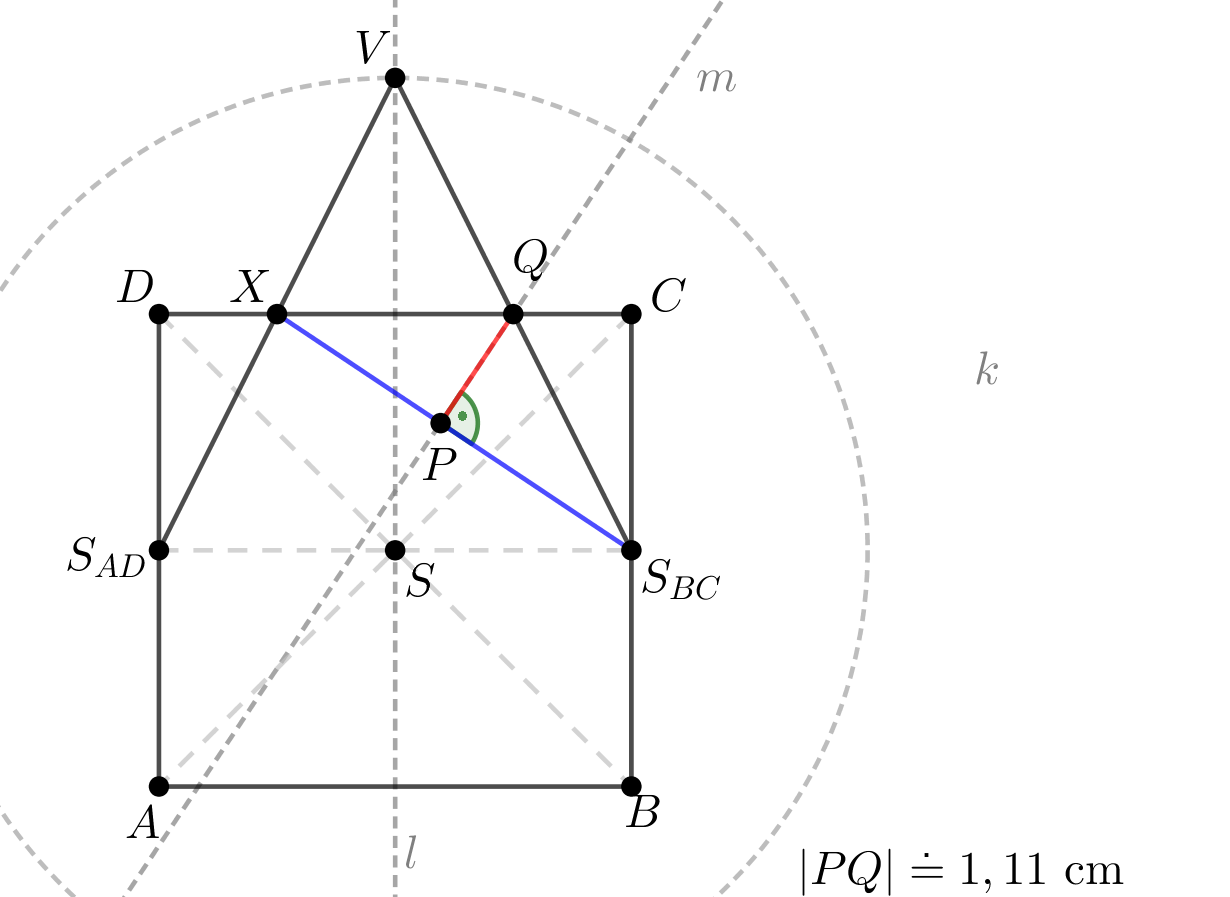
Syntetické konstrukční řešení
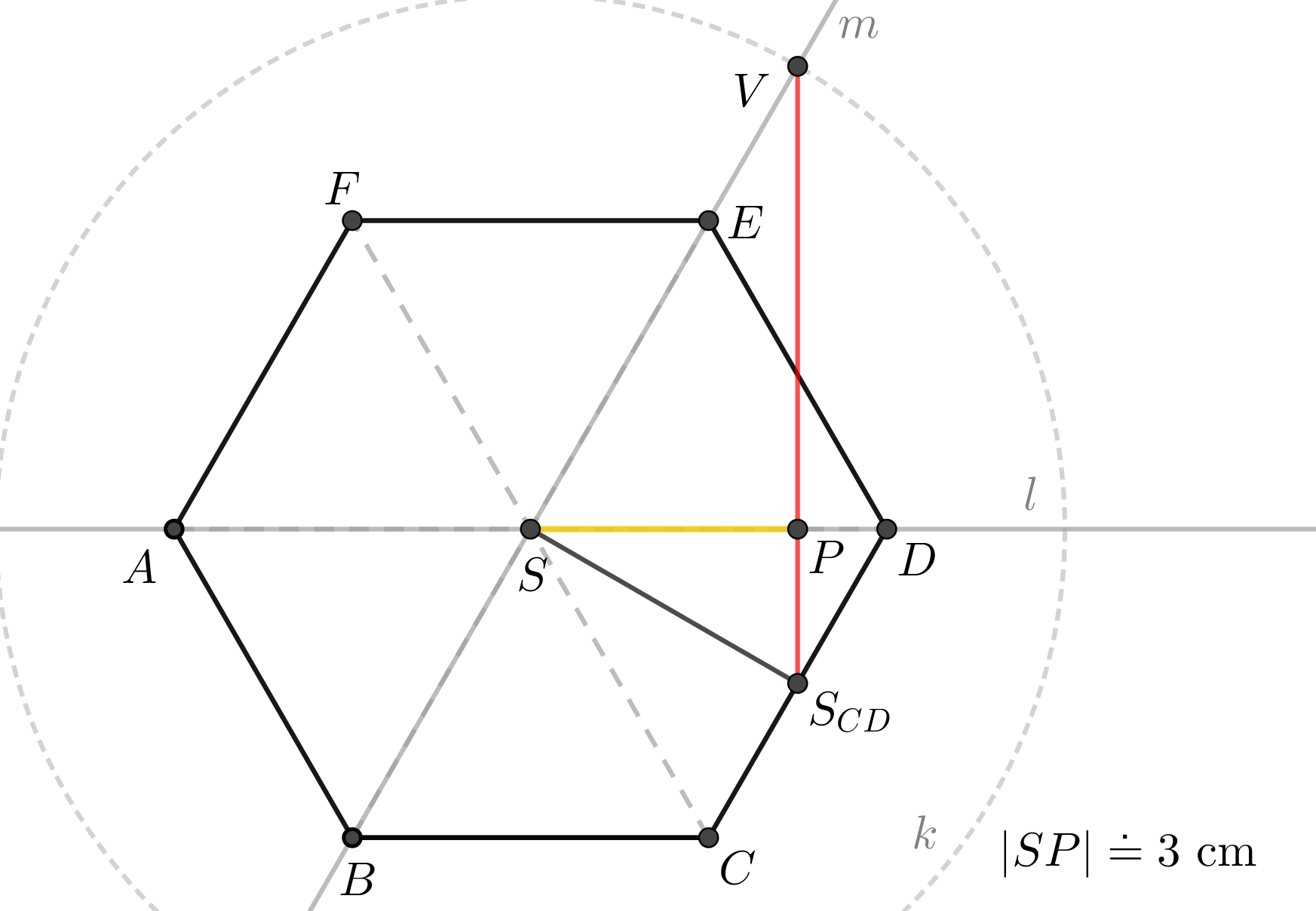
Je dán pravidelný šestiboký jehlan \(ABCDEFV\) s podstavou \(ABCDEF\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 6\mbox{ cm}\). Určete vzdálenost bodu \(S\) od roviny boční stěny jehlanu.
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
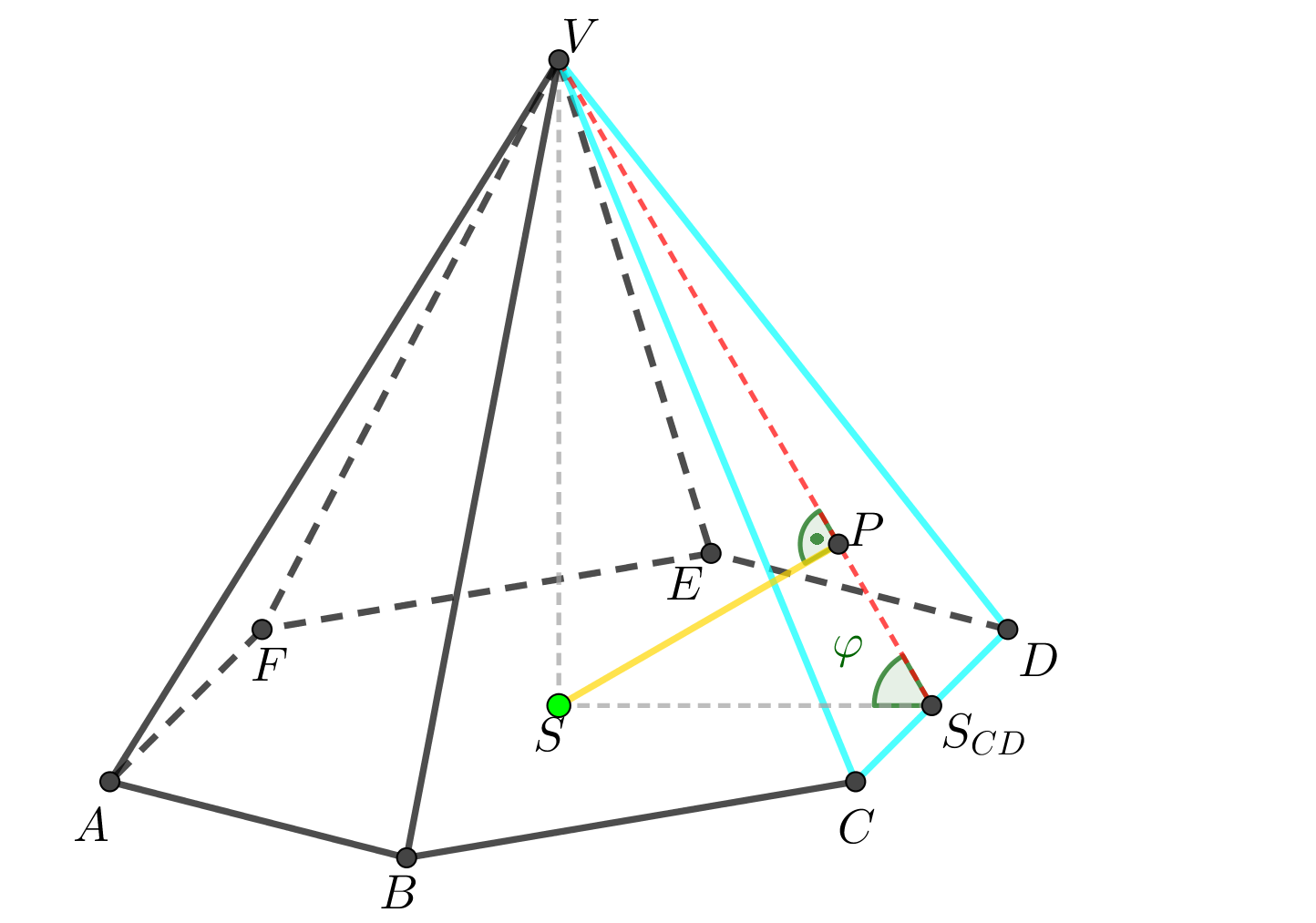
Syntetické konstrukční řešení