Příklady k procvičení:
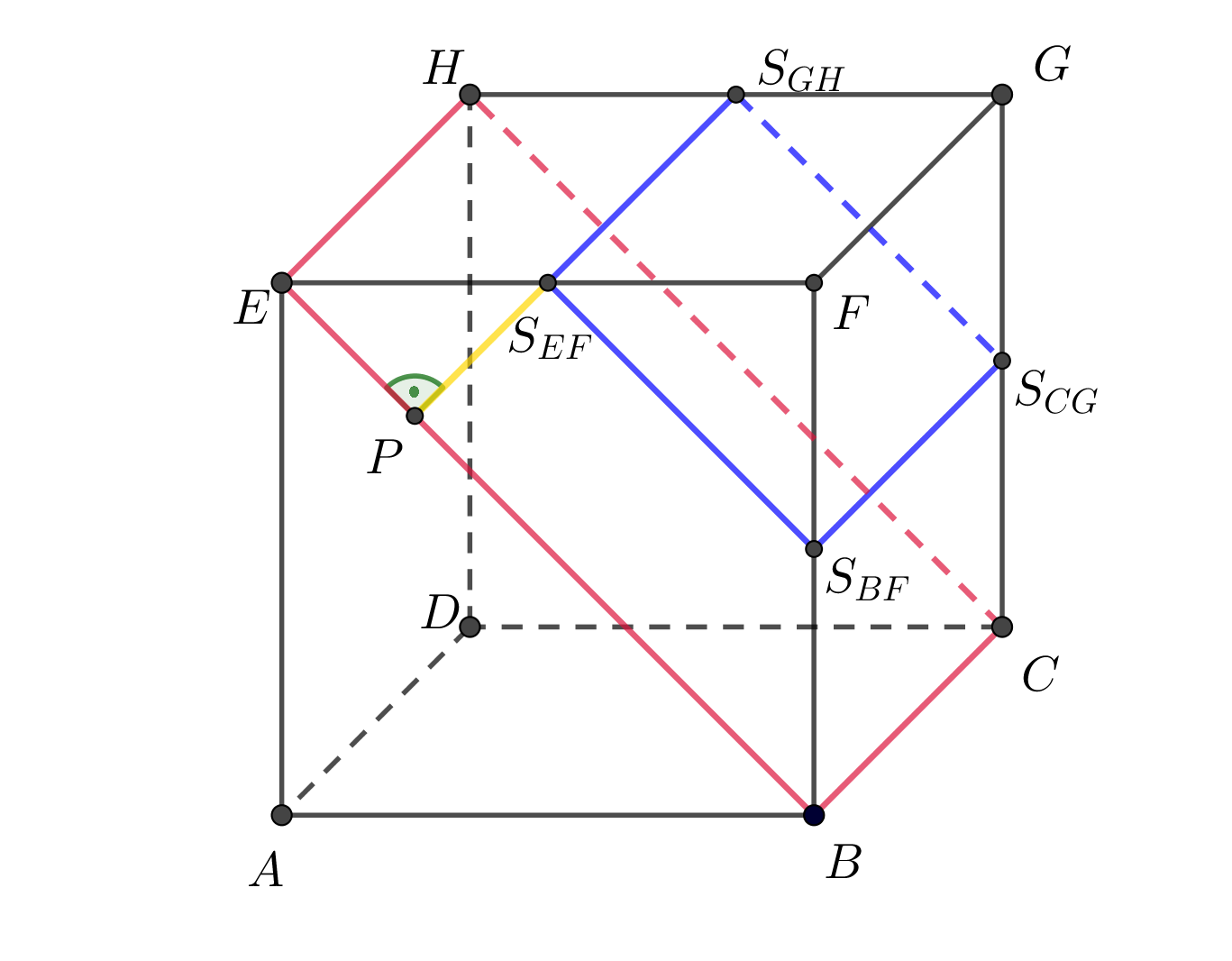
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost rovin \(EBC\) a \(S_{EF}S_{BF}S_{CG}\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Vzdálenost rovin \(EBC\) , \(S_{EF}S_{BF}S_{CG}\) je rovna vzdálenosti libovolného bodu roviny \(S_{EF}S_{BF}S_{CG}\) od roviny \(EBC\):
\[d(S_{EF},\leftrightarrow EBC)=\frac{|ax_{S_{EF}}+by_{S_{EF}}+cz_{S_{EF}}+d|}{\sqrt{a^2+b^2+c^2}}\] Rovina \(EBC\) má obecnou rovnici \(ax+by+cz+d=0\) a \(S_{EF}=[x_{S_{EF}};y_{S_{EF}};z_{S_{EF}}]=[2;0;4]\) je námi zvolený libovolný bod roviny \(S_{EF}S_{BF}S_{CG}\).
Potřebujeme tedy určit normálový vektor roviny \(EBC\).
Normálový vektor lze určit pomocí dvou směrových vektorů této roviny, například:
\[\overrightarrow{BE}=(-4;0;4),\quad\overrightarrow{BC}=(0;4;0)\] Určeme normálový vektor roviny \(EBC\) \[\begin{eqnarray*}\overrightarrow{n_{EBC}}&=&\overrightarrow{BE}\times\overrightarrow{BC}\\
&=&(0\cdot 0-4\cdot 4;4\cdot 0-(-4)\cdot 0;(-4)\cdot 4-0\cdot 0)\\
&=&(-16;0;-16)\sim(1;0;1)\end{eqnarray*}\] Dosazením souřadnic bodu \(B\) do rovnice \(x+y+d=0\) vypočítáme \(d=-4\).
Nyní můžeme dosadit do výše uvedeného vztahu pro výpočet vzdálenosti bodu od roviny:
\[d(S_{EF},\leftrightarrow EBC)=\frac{|1\cdot 2+0\cdot 0+1\cdot 4-4|}{\sqrt{1^2+0^2+1^2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\doteq 1,41\mbox{ cm}\]
Syntetické početní řešení

K řešení využijeme trojúhelník \(EPS_{EF}\), kde bod \(P\) je patou výšky lichoběžníku \(EBS_{BF}S_{EF}\). V tomto trojúhelníku známe délku strany \(ES_{EF}\) (\(|ES_{EF}|=2\mbox{ cm}\)) a velikost úhlu \(S_{EF}EP\).
Velikost úhlu \(S_{EF}EP\) je rovna polovině velikosti úhlu \(FEA\), tj. \(|\angle S_{EF}EP|=45^\circ\).
Použijeme tedy goniometrickou funkci sinus:
\[\sin(\angle S_{EF}EP)=\frac{|PS_{EF}|}{|ES_{EF}|}\Rightarrow |PS_{EF}|=|ES_{EF}|\cdot\sin(\angle S_{EF}EP) = 2\sin45^\circ=\sqrt{2}\doteq 1,41\mbox{ cm}\]
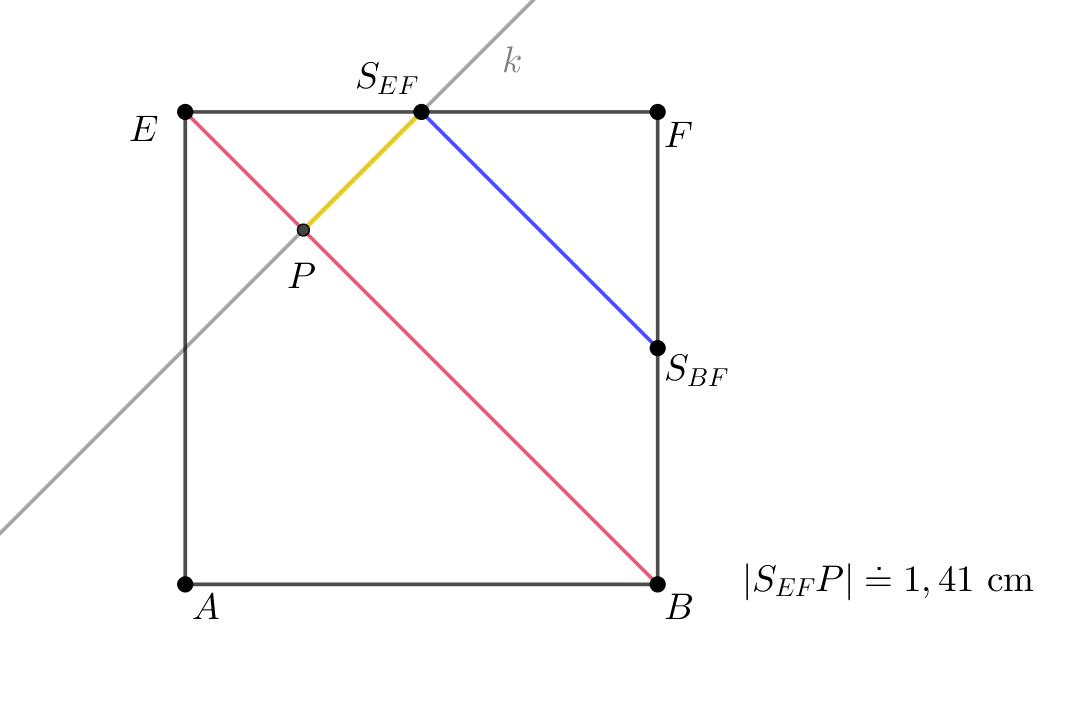
Syntetické konstrukční řešení

Zápis konstrukce:
\(\mbox{1) čtverec } ABFE; |AB|=4 \mbox{ cm}\)
\(\mbox{2) } S_{EF}; S_{EF}\in EF \wedge |ES_{EF}|=|S_{EF}F|\)
\(\mbox{3) } S_{BF}; S_{BF}\in BF \wedge |BS_{BF}|=|S_{BF}F|\)
\(\mbox{4) } \leftrightarrow k; k\perp \overline{EB} \wedge S_{EF}\in k\)
\(\mbox{5) } P; \overline{EB}\cap k = \{P\} \)
Provedením konstrukce jsme získali vzdálenost bodů \(P\) a \(S_{EF}\), čímž jsme sestrojili vzdálenost rovin \(EBC\) a \(S_{EF}S_{BF}S_{CG}\).
