Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete odchylku přímky \(AB\) od přímky \(S_{BF}E\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení
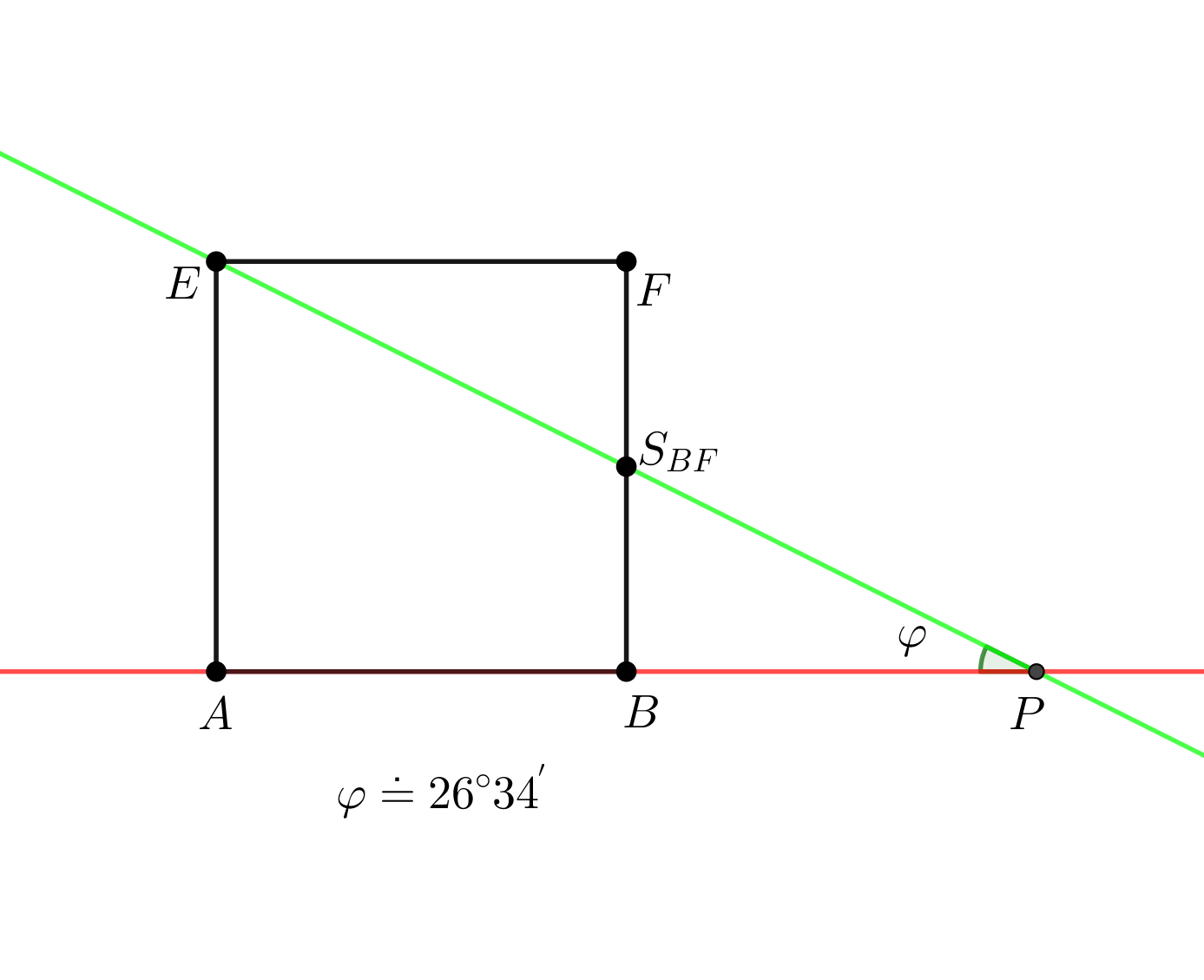
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete odchylku přímek \(S_{AE}B\), \(S_{BF}G\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Pro směrové vektory přímek platí: \[\overrightarrow{BS_{AE}}=(-4;0;2),\quad\overrightarrow{S_{BF}G}=(0;4;2)\] Dosaďme nyní do vztahu pro odchylku přímek: \[\cos\varphi=\frac{|(-4;0;2)\cdot(0;4;2)|}{|(-4;0;2)|\cdot|(0;4;2)|}=\frac{|2\cdot 2|}{\sqrt{(-4)^2+2^2}\cdot\sqrt{4^2+2^2}}=\frac{|4|}{4\cdot 5}=\frac{1}{5}\Rightarrow\varphi\doteq 78^\circ 28^{'}\]
Syntetické početní řešení

Syntetické konstrukční řešení

Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 5\mbox{ cm}\). Určete odchylku přímek \(AS_{CD}\), \(CV\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení

Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete odchylku přímek \(BE\), \(AH\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení

Syntetické konstrukční řešení

