Geometrická zobrazení

$\begin{align} \end{align}$

Příklad 4

Narýsujte lichoběžník $ABCD$ se základnami $AB$ a $CD$ , znáte-li délku strany $c$ , délku výšky $v_c$ lichoběžníka, velikost $\alpha$ úhlu $DAB$ a velikost střední příčky lichoběžníka, jež je $5/3\;c$ . Předpokládejme, že $\alpha > 0°$ , $c > 0$ , $v_c > 0$ .

Rozbor

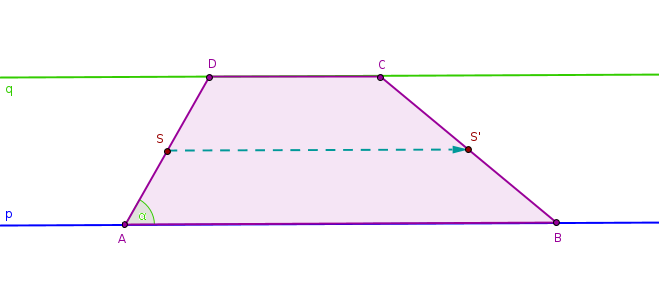
Obr. 3.3.3 - Náčrtek příkladu 4

Předpokládejme, že vrcholy takového lichoběžníka leží na přímkách $p$ , $q$ , kde $p \parallel q$ a $|pq|=v_c$ .
Přímo ze zadání snadno sestrojíme některé vrcholy lichoběžníka, konkrétně vrcholy $A$ , $C$ a $D$ . Zbývá získat bod $B$ .

Střední příčka lichoběžníka je úsečka, která spojuje středy jeho ramen. Budeme-li se na střední příčku dívat jako na orientovanou úsečku s počátečním bodem $S$ ve středu strany $AD$ a koncovým bodem $S'$ ve středu strany $BD$ , pak se bod $S$ zobrazí na bod $S'$ v posunutí určeném touto orientovanou úsečkou.
Využijeme již zkonstruovaného bodu, například bodu $D$ . (Využijeme tedy toho, že úsečku délky $c$ už máme narýsovanou.) Sestrojíme pomocnou orientovanou úsečku DY délky střední příčky, kde bod $Y$ bude ležet na přímce $q$ . Tak zajistíme, že orientovaná úsečka DY bude rovnoběžná se střední příčkou lichoběžníka.
Střed $S'$ strany $BC$ získáme jako obraz středu $S$ strany $AD$ v posunutí určeném orientovanou úsečkou DY.
Bod $S'$ a bod $C$ nám určí přímku, na které bude ležet strana $BC$ , bod $B$ je průsečík této přímky a přímky $p$ .