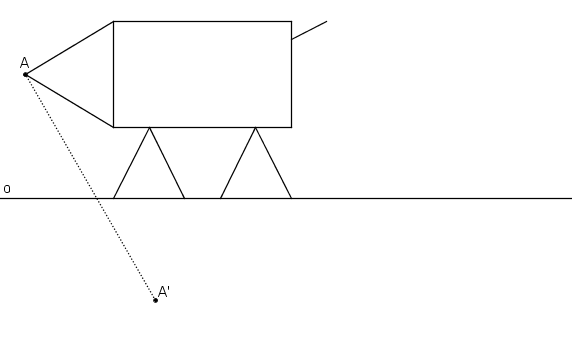
Dourčování prvků
Sadu úloh na procvičení najdete zde: Zadání, Řešení.
Příklad: V OA (o, AA´) určete obrazy bodů (B´, C).
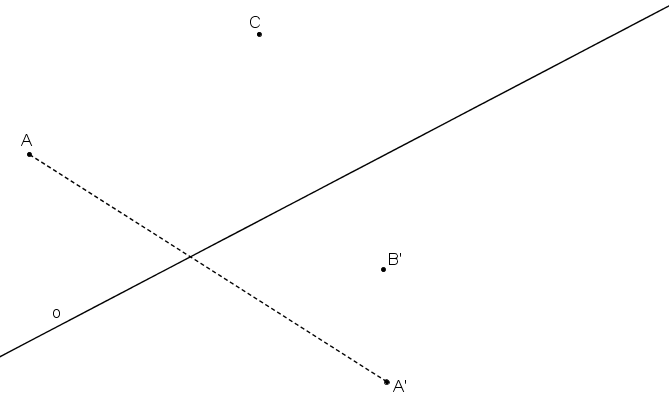
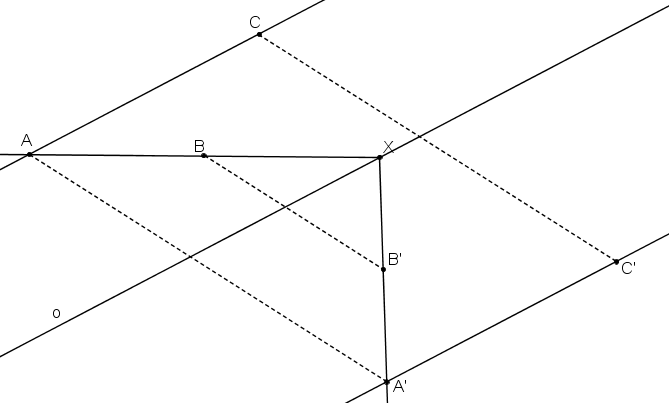
Obrazy bodů B, C.
Příklad: V OA (o, AA´) určete obrazy přímek b, c´.
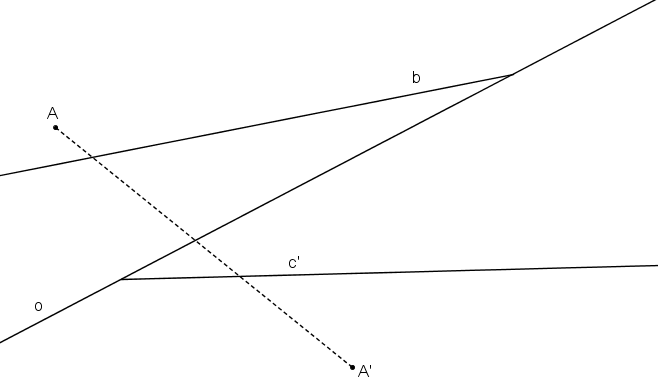
Řešení: OA je dána (o, AA´). Určete obrazy přímek b, c´.
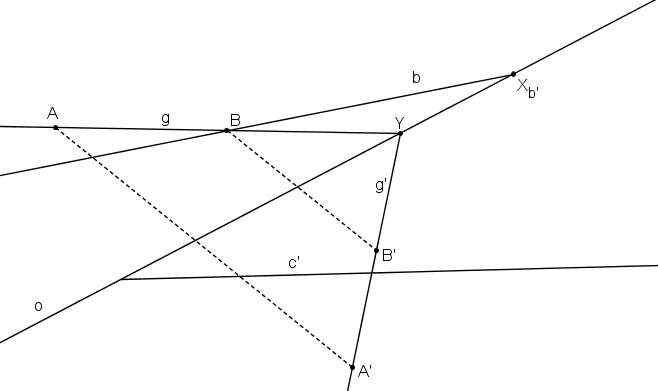
Nejprve určíme obraz přímky b. Na přímce b libovolně zvolíme bod B a určíme jeho obraz B´.
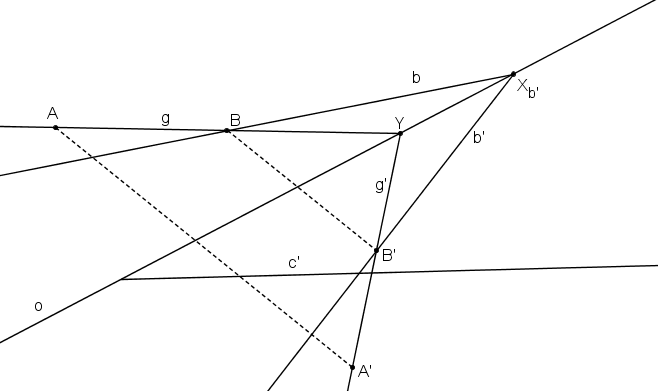
Přímka b´ prochází bodem B´ a svým samodružným bodem.

Na přímce c´ zvolíme libovolně bod C´ a určíme jeho obraz.
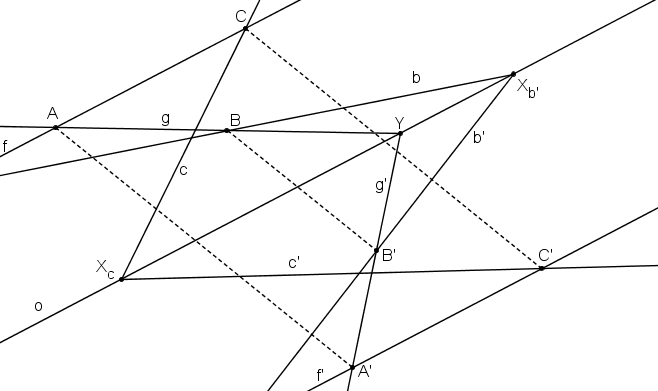
Přímka c prochází bodem C a svým samodružným bodem.
Příklad: V OA (o, AA´) určete obraz různoběžných přímek b, c.
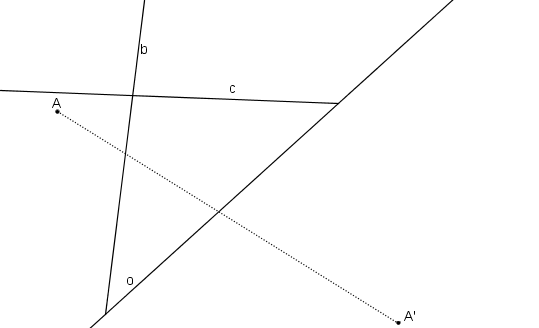
Obrazy různoběžných přímek b, c.

Příklad: V OA (o, AA´) určete obraz rovnoběžných přímek b, c.

Obrazy rovnoběžných přímek b, c.
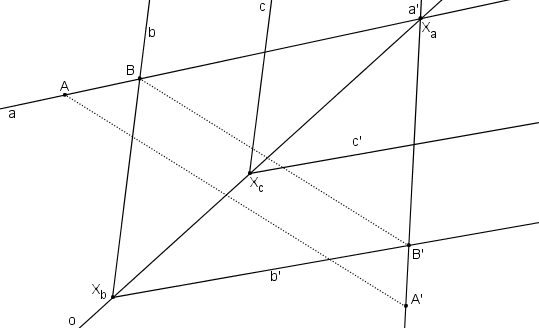
Příklad: V OA (o, AA´) určete obraz pravidelného pětiúhelníka ABCDE.
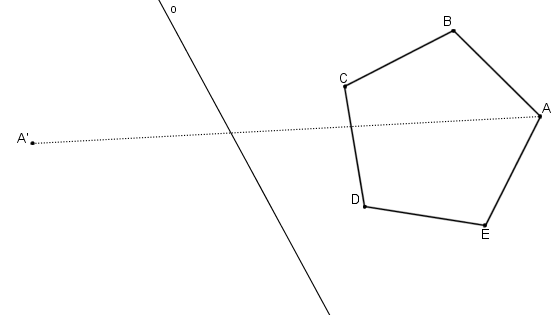
Obraz pětiúhelníka.
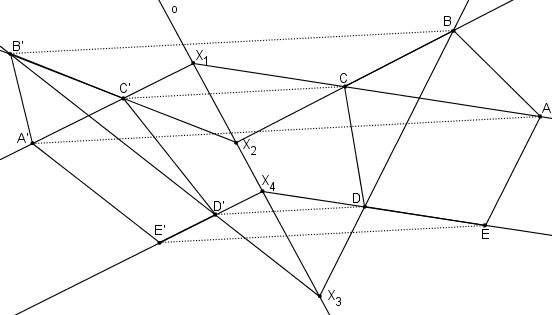
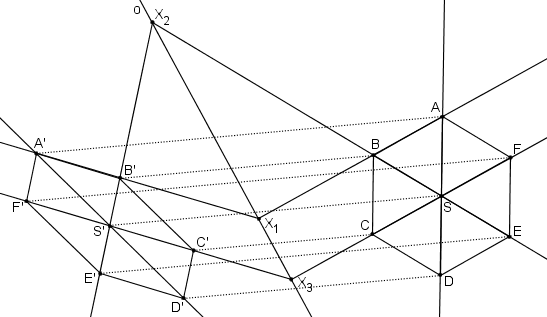
Příklad: V OA (o, AA´) určete obraz pravidelného šestiúhelníka ABCDEF.
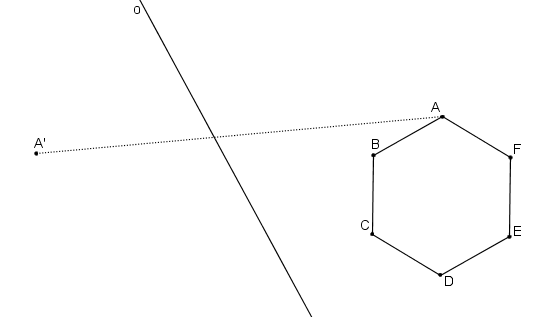
Obraz šestiúhelníka.
Příklad: Je dán rovnoběžník ABCD a osa afinity o. Dourčete osovou afinitu (body AA´) tak, aby byl obrazem rovnoběžníku obdélník A´B´C´D´.
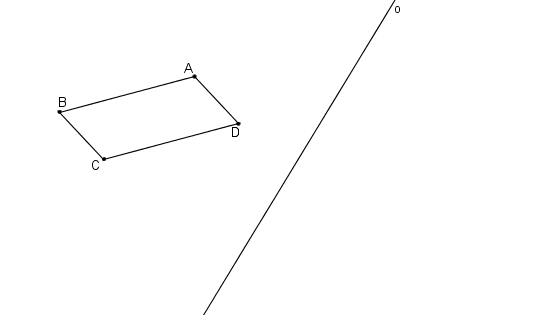
Řešení: Je dán rovnoběžník ABCD a osa afinity o.
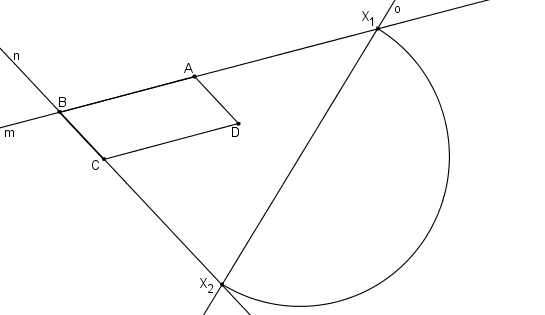
Úhel mezi přímkami AB, BC se má zobrazit na pravý úhel. Bod B´ proto leží na Thaletově kružnici sestrojené nad samodružnými body přímek AB, BC.

Na Thaletově kružnici můžeme bod B´ zvolit libovolně.
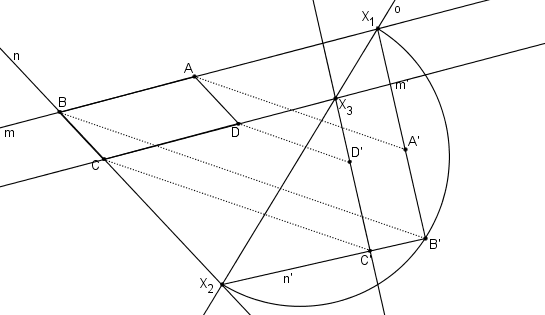
Pomocí OA (o, BB´) dourčíme body A´, C´, D´.

Rovnoběžník ABCD se zobrazil obdélník A´B´C´D´.
Příklad: Je dán rovnoběžník ABCD a osa afinity o. Dourčete osovou afinitu (body AA´) tak, aby byl obrazem rovnoběžníku čtverec A´B´C´D´.
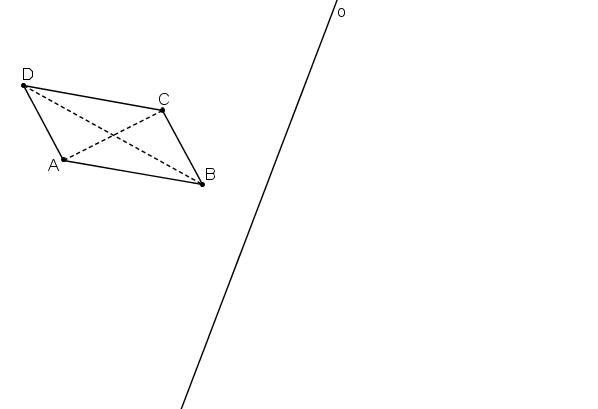
Řešení: Je dán rovnoběžník ABCD a osa afinity o.
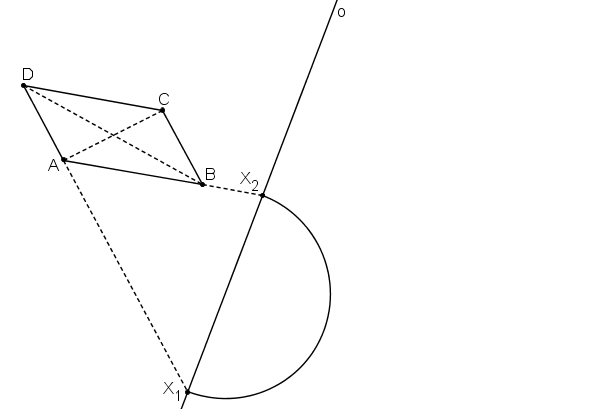
Úhel mezi přímkami AB, AD se má zobrazit na pravý úhel. Bod A´ proto leží na Thaletově kružnici sestrojené nad samodružnými body přímek AB, AD.

Úhel mezi přímkami AB, AC se má zobrazit na úhel rovný 45°. Bod A´ proto leží na oblouku se středem v bodě O a poloměrem OX3. Pro libovolný bod J na oblouku platí, že úhel X2JX3 je roven 45°.
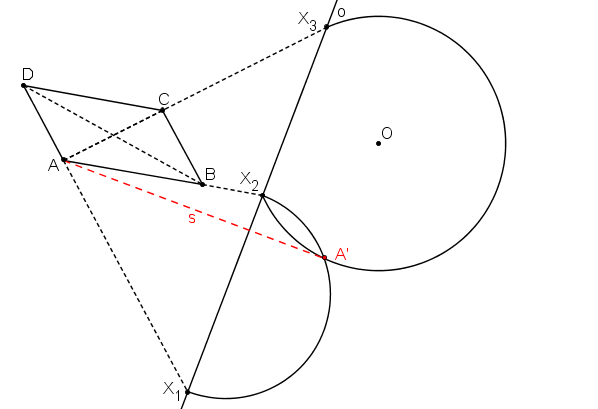
Průsečík oblouku se středem v bodě O a poloměrem OX3 a thaletovy kružnice nad samodružnými body přímek AB, AD je hledaný bod A´.

Pomocí OA sestrojíme obrazy bodů B, C, D.
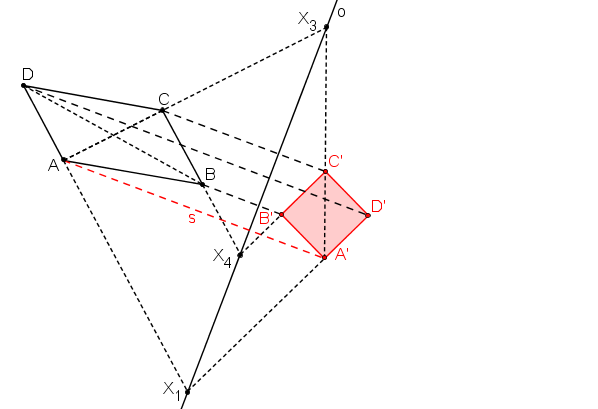
Rovnoběžník ABCD se zobrazil na čtverec A´B´C´D´.
Příklad: V OA (o, SS´) určete obraz kružnice k.
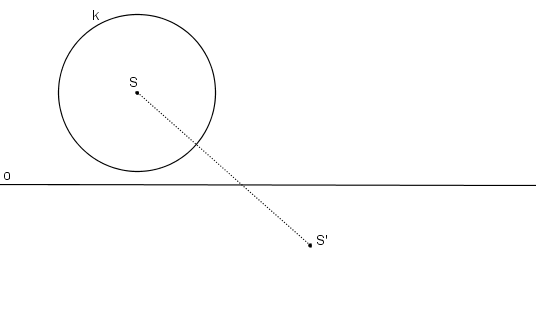
Obraz kružnice.
Příklad: Jsou dány neomezené sdružené průměry elipsy a, b a dva body na elipse P, Q. Sestrojte elipsu.
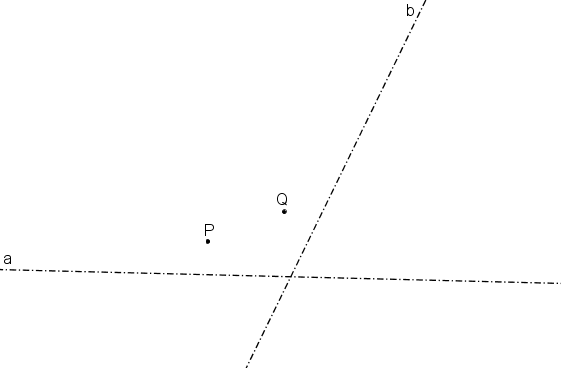
Řešení: Jsou dány neomezené sdružené průměry elipsy a, b a dva body na elipse P, Q. Sestrojte elipsu.
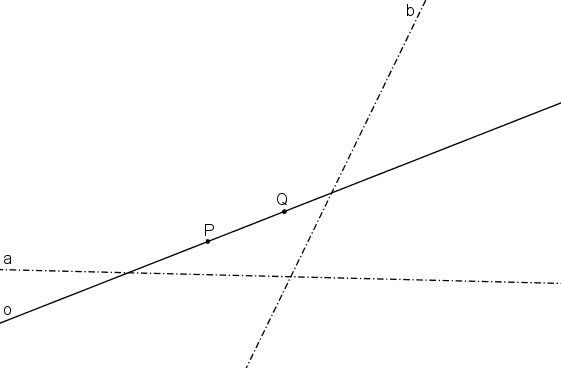
Vhodně zvolíme osovou afinitu tak, aby obrazem elipsy byla kružnice. Body P, Q označíme za samodružné. Určují proto osu afinity o.

Přímky a, b jsou sdružené průměry. Jejich průsečík označme O. Chceme, aby se úhel mezi přímkami a, b zobrazil na pravý. Bod O´ proto leží na Thaletově kružnici sestrojené nad samodružnými body X, Y přímek a, b.
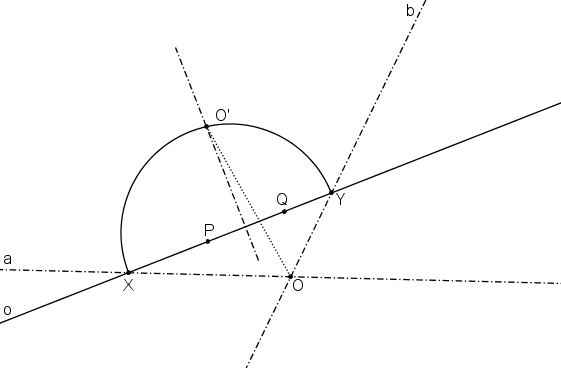
Kružnice k´ musí procházet body P, Q. Střed O´ kružnice k´ proto leží na ose úsečky PQ.
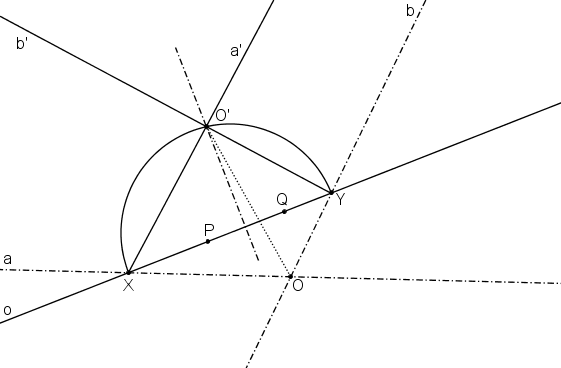
Obrazy a´, b´ přímek a, b jsou určeny body XO´, YO´.

Přímka a´ (resp. b´) protíná kružnici k´ (O´, |O´P|) v bodech M´, N´ (resp. K´, L´).

Pomocí OA (o, OO´) nalezneme body K, L, M, N, které tvoří sdružené průměry elipsy.
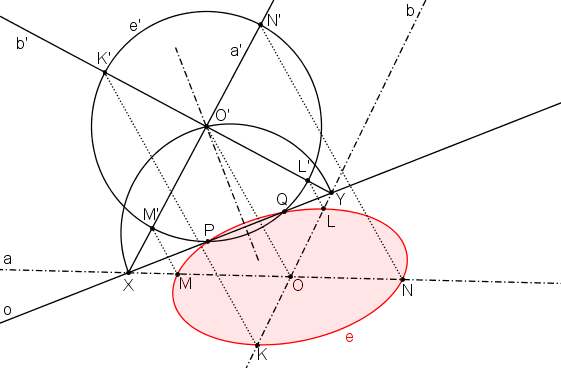
Známe-li sdružené průměry, můžeme vyrýsovat elipsu e.
Příklad: V OA (o, AA´) určete obraz nápisu AFINITA.

Příklad: V OA (o, AA´) určete obraz domečku.
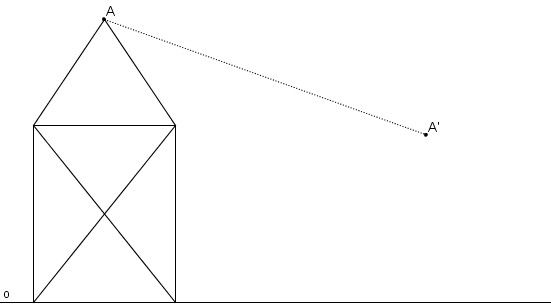
Příklad: V OA (o, AA´) určete obraz prasátka.