Sin curve

The (topologist's) sin curve is defined by

1. is irreducible between points and , . It has exactly three end points and two arc components.
2. It is one of the simplest arc-like continua.
3. It is a compactification of a ray with remainder an arc.
4. It has the periodic-recurrent property [Charatonik et al. 1997b, Corollary 5.10, p. 117].
5. The only possible confluent nondegenerate images of are an arc and a continuum homeomorphic to [Nadler 1977a].
6. The hyperspace of all subcontinua of is homeomorphic to the cone over [Nadler 1977b].

See Figure A.

Figure 4.1.1: ( A ) sin curve

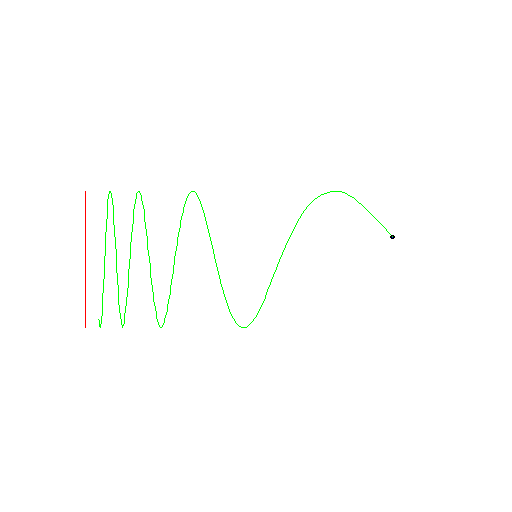There are many variations of the sin curve. Some of them are pictured below. See Figure B-C.

Figure 4.1.1: ( B ) union of two sin curves

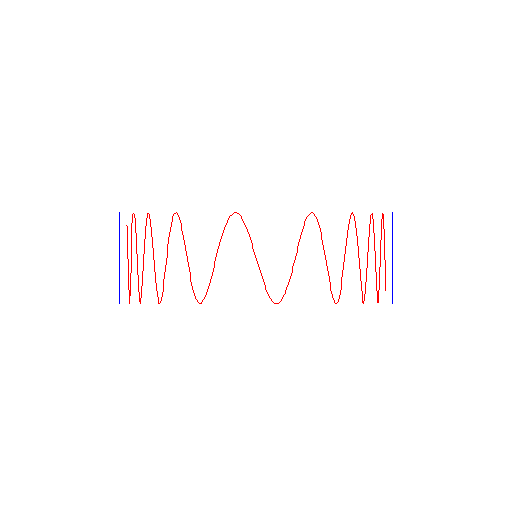Figure 4.1.1: ( C ) union of two sin curves

Here you can find source files of this example.

Here you can check the table of properties of individual continua.

Here you can read Notes or write to Notes ies of individual continua.