next up previous contents index
Next: Self-homeomorphic dendrites Up: Dendrites Previous: Other universal dendrites

The dendrite P$

In connection with the characterization of dendrites having closed set of their end points (see Property 2 in 1.3.4 above) the classes of those dendrites that do not contain a copy of F_\omega $ and those that do not contain a copy of the comb W$ are of some interest (see [Arévalo et al. 2001, p. 8]). The first one is just the class of dendrites with finite orders of ramification points, and it is known to have a universal element according to Property 4 in 1.3.8. The other class has also a universal element P$. Its construction, given in [Arévalo et al. 2001, p. 9] is the following.

Let p$ be any point in the plane \mathbb{R}^2$ and let p_1, p_2, \dots$ be a sequence of points in \mathbb{R}^2$ tending to p$ and such that no three of the points p, p_1, p_2, \dots$ are collinear. Define P_1 = \bigcup \{\overline{pp_n}: n \in \mathbb{N}\}$. Then P_1$ is homeomorphic to F_\omega $. For every n, m \in \mathbb{N}$, let p_{nm}$ be a point in \mathbb{R}^2 \setminus P_1$ such that for any fixed n$ the sequence p_{n1}, p_{n2}, \dots$ tends to p_n$, no three of the points p_n, p_{n1}, p_{n2}, \dots$ are collinear, and that the continuum P_2 = P_1 \cup \bigcup \{\overline{p_np_{nm}}: n, m \in \mathbb{N}\}$ is a dendrite. We continue constructing dendrites P_3, P_4, \dots$ in the same manner, such that we get an increasing sequence of dendrites P_1 \subset P_2 \subset P_3 \subset \dots \subset P_n \subset P_{n+1} \subset \dots$ in \mathbb{R}^2$ having the property that the closure of their union is also a dendrite. Finally define

\displaystyle P = \mathrm{cl}\,(\bigcup\{P_n: n \in \mathbb{N}\}). $

The following properties of the dendrite P$ are proved in [Arévalo et al. 2001, Theorems 4.5 and 4.6, p. 10].

  1. A dendrite X$ is homeomorphic to the dendrite P$ if and only if each of the following conditions is satisfied:
    1. X$ contains no copy of W$;
    2. the set of all end points of X$ is contained in the closure of the set of all ramification points of X$;
    3. all ramification points of X$ are of order \omega$.
  2. The dendrite P$ is universal in the class of all dendrites containing no copy of W$.

See Figure A.

Figure 1.3.9: ( A ) dendrite P$
A.gif

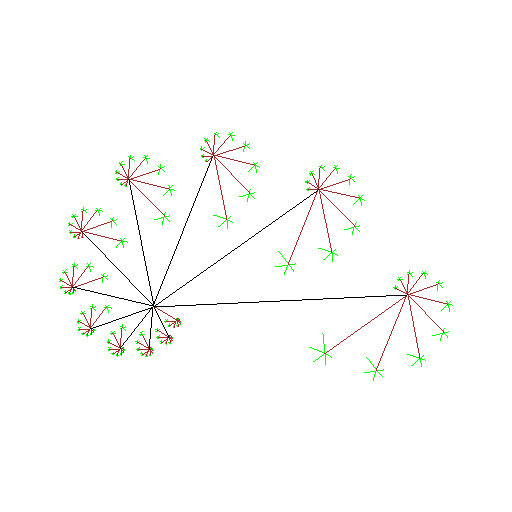Figure: ( AA ) dendrite P$ - an animation
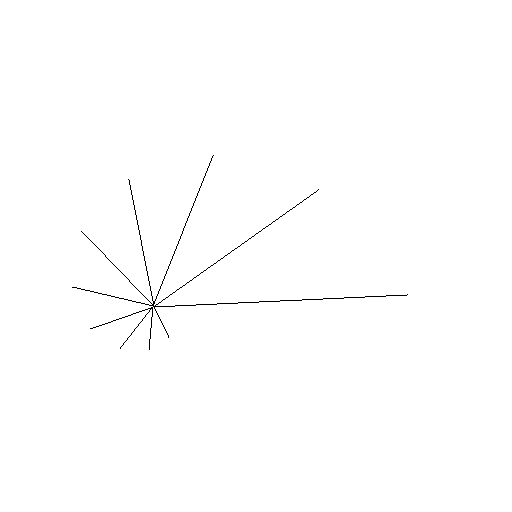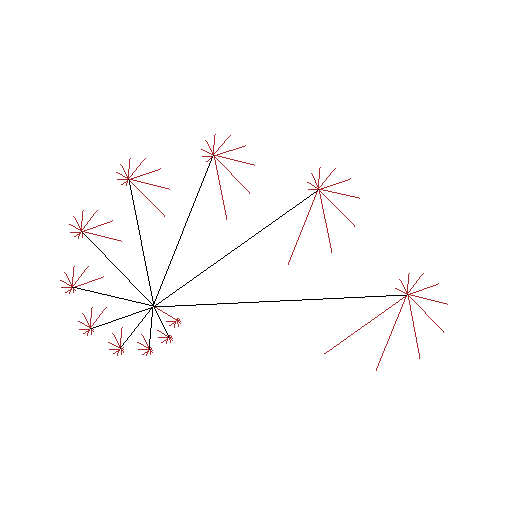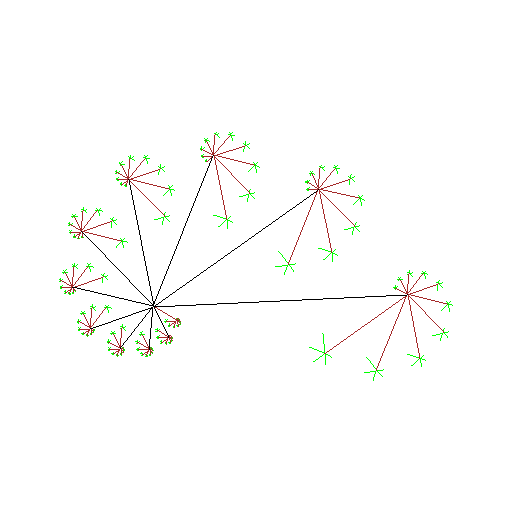AA.gif

Here you can find source files of this example.

Here you can check the table of properties of individual continua.

Here you can read Notes or write to Notes ies of individual continua.
next up previous contents index
Next: Self-homeomorphic dendrites Up: Dendrites Previous: Other universal dendrites
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30