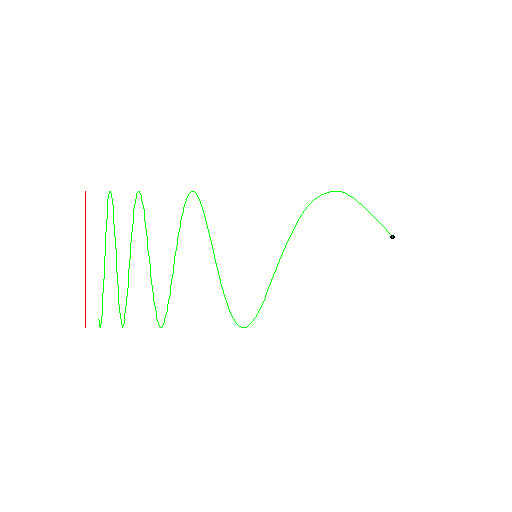Next: Open Sin
Up: Arc-like continua
Previous: Arc-like continua
The Topologist's Sin Curve is well known
continuum which is not arcwise connected. The continuum is defined
by the union
It has just two path components. More we can find in
[74, p.137] .
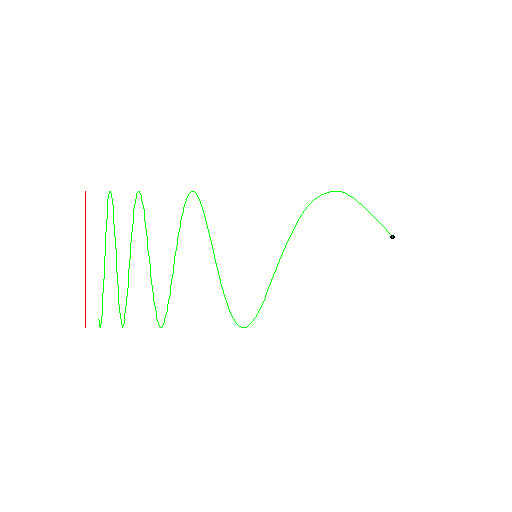
Figure (
A
)
Topologist's Sin Curve
Source files:
a.eps .
a.gif .
example.htm .
figure.mws .
latex.tex .
title.txt .
Here you can
read Notes or
write to Notes.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21