




Next: weak cut point
Up: Definitions
Previous: uniquely arcwise connected
Let a class 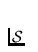 of spaces be given. A member U of
of spaces be given. A member U of 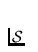 is
said to be universal for
is
said to be universal for
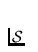 if every member of
if every member of 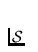 can be embedded in U, i.e., if for every
can be embedded in U, i.e., if for every
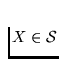 there
exists a homeomorphism
there
exists a homeomorphism
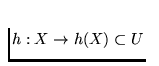 . Accordingly, a dendrite is
said to be universal if it contains a homeomorphic image of any
other dendrite.
. Accordingly, a dendrite is
said to be universal if it contains a homeomorphic image of any
other dendrite.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
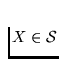 there
exists a homeomorphism
there
exists a homeomorphism
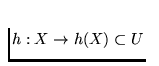 . Accordingly, a dendrite is
said to be universal if it contains a homeomorphic image of any
other dendrite.
. Accordingly, a dendrite is
said to be universal if it contains a homeomorphic image of any
other dendrite.