




Next: hereditarily locally connected
Up: Definitions
Previous: hereditarily equivalent
a continuum X is said to be
hereditarily indecomposable provided that each of its
subcontinua is indecomposable,
that is, for each subcontinuum 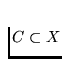 and for every continua A and
B such that
and for every continua A and
B such that  we have either A = C or B = C.
we have either A = C or B = C.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
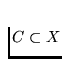 and for every continua A and
B such that
and for every continua A and
B such that  we have either A = C or B = C.
we have either A = C or B = C.