




Next: F-equivalent
Up: Definitions
Previous: end point
Let 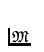 be a class of mappings. Two spaces X and Y are said to
be equivalent with respect to
be a class of mappings. Two spaces X and Y are said to
be equivalent with respect to
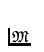 (shortly
(shortly
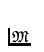 - equivalent) if there are two mappings, both in
- equivalent) if there are two mappings, both in
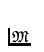 , one from X onto Y and the other from Y onto X. If
, one from X onto Y and the other from Y onto X. If
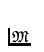 means the class of monotone mappings, we say that X and Y
are monotonely equivalent.
means the class of monotone mappings, we say that X and Y
are monotonely equivalent.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21