




Next: cyclic element
Up: Definitions
Previous: cut point
Let X be a continuum. Define
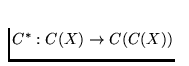 by
C*(A) =
C(A). It is known that for any continuum X the function C* is upper
semi-continuous, [64, Theorem 15.2, p. 514], and it is continuous on
a dense
by
C*(A) =
C(A). It is known that for any continuum X the function C* is upper
semi-continuous, [64, Theorem 15.2, p. 514], and it is continuous on
a dense 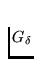 subset of C(X), [64, Corollary 15.3, p. 515].
A continuum X is said to be C*-smooth at
subset of C(X), [64, Corollary 15.3, p. 515].
A continuum X is said to be C*-smooth at 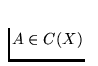 provided that
the function C* is continuous at A. A continuum X is said to be
C*-smooth provided that the function C* is continuous on
C(X), i.e., at each
provided that
the function C* is continuous at A. A continuum X is said to be
C*-smooth provided that the function C* is continuous on
C(X), i.e., at each 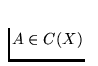 (see [64, Definition 5.15, p. 517]).
(see [64, Definition 5.15, p. 517]).
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
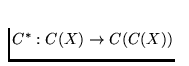 by
C*(A) =
C(A). It is known that for any continuum X the function C* is upper
semi-continuous, [64, Theorem 15.2, p. 514], and it is continuous on
a dense
by
C*(A) =
C(A). It is known that for any continuum X the function C* is upper
semi-continuous, [64, Theorem 15.2, p. 514], and it is continuous on
a dense 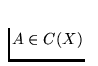 provided that
the function C* is continuous at A. A continuum X is said to be
C*-smooth provided that the function C* is continuous on
C(X), i.e., at each
provided that
the function C* is continuous at A. A continuum X is said to be
C*-smooth provided that the function C* is continuous on
C(X), i.e., at each 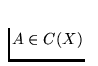 (see [64, Definition 5.15, p. 517]).
(see [64, Definition 5.15, p. 517]).