




Next: arc-structure
Up: Definitions
Previous: arc
Given a continuum X with an arc-structure A, the pair
(X,A) (see arc-structure) is said to be arc-smooth at a point 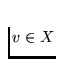 provided that the induced function
provided that the induced function
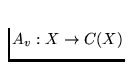 defined by
Av (x) =
A(v,x) is continuous. Then the point v is called an initial
point of (X,A). The pair (X,A) is said to be arc-smooth
provided that there exists a point in X at which (X,A) is arc-smooth. An
arbitrary space X is said to be arc-smooth at a point
defined by
Av (x) =
A(v,x) is continuous. Then the point v is called an initial
point of (X,A). The pair (X,A) is said to be arc-smooth
provided that there exists a point in X at which (X,A) is arc-smooth. An
arbitrary space X is said to be arc-smooth at a point 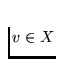 provided that there exists an arc-structure A on X for which (X,A) is
arc-smooth at v. The space X is said to be arc-smooth if it is
arc-smooth at some point (see [42, p. 546]). Note that a dendroid is
smooth if and only if it is arc-smooth.
provided that there exists an arc-structure A on X for which (X,A) is
arc-smooth at v. The space X is said to be arc-smooth if it is
arc-smooth at some point (see [42, p. 546]). Note that a dendroid is
smooth if and only if it is arc-smooth.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
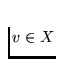 provided that the induced function
provided that the induced function
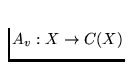 defined by
Av (x) =
A(v,x) is continuous. Then the point v is called an initial
point of (X,A). The pair (X,A) is said to be arc-smooth
provided that there exists a point in X at which (X,A) is arc-smooth. An
arbitrary space X is said to be arc-smooth at a point
defined by
Av (x) =
A(v,x) is continuous. Then the point v is called an initial
point of (X,A). The pair (X,A) is said to be arc-smooth
provided that there exists a point in X at which (X,A) is arc-smooth. An
arbitrary space X is said to be arc-smooth at a point 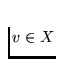 provided that there exists an arc-structure A on X for which (X,A) is
arc-smooth at v. The space X is said to be arc-smooth if it is
arc-smooth at some point (see [42, p. 546]). Note that a dendroid is
smooth if and only if it is arc-smooth.
provided that there exists an arc-structure A on X for which (X,A) is
arc-smooth at v. The space X is said to be arc-smooth if it is
arc-smooth at some point (see [42, p. 546]). Note that a dendroid is
smooth if and only if it is arc-smooth.