




Next: almost chainable
Up: Definitions
Previous: absolutely terminal continuum
A continuum X is said to be acyclic provided that each
mapping from X into the unit circle 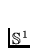 is homotopic to a constant
mapping, i.e., for all mappings
is homotopic to a constant
mapping, i.e., for all mappings
 and
and
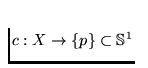 there exists a mapping
there exists a mapping
![$h: X \times [0,1] \to \mathbb{S}^1$](img112.gif) such that for each
point
such that for each
point 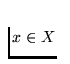 we have h(x,0) = f(x) and h(x,1) = c(x).
we have h(x,0) = f(x) and h(x,1) = c(x).
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
 and
and
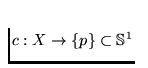 there exists a mapping
there exists a mapping
![$h: X \times [0,1] \to \mathbb{S}^1$](img112.gif) such that for each
point
such that for each
point 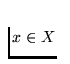 we have h(x,0) = f(x) and h(x,1) = c(x).
we have h(x,0) = f(x) and h(x,1) = c(x).