Zpet na domovskou stranku
Seznam publikaci
Otevrene problemy

Kompakty ve funkcionalni analyze

Nektere okruhy vyzkumu
Mozny zdroj temat pro diplomove prace Predpokladane znalosti:

topologie - metricke a topologicke prostory, spojita zobrazeni, souciny, kompaktni prostory
funkcionalni analyza - Banachovy prostory, slabe a slabe* topologie
teorie mnozin - zakladni veci o ordinalnich a kardinalnich cislech

Jiz od sedesatych let se zkoumaly kompaktni prostory prirozene se vyskytujici ve funkcionalni analyze, zvlaste v teorii Banachovych prostoru. To vedlo k zavadeni a studiu ruznych trid kompaktnich prostoru, ktere, jak se ukazalo, maji zajimavou strukturu a mnoho peknych vlastnosti. Tyto tridy, rozlicne motivovane, nejsou linearne usporadane, ale tvori slozitejsi hierarchickou strukturu. Mnohe o techto tridach a jejich aplikacich se lze docist v knihach

R.Deville, G.Godefroy and V.Zizler, Smoothness and renorming in Banach spaces, Pitman Monographs, 1993.
M.Fabian, Gateaux differentiability of convex functions and topology: weak Asplund spaces, Wiley-Interscience, New York, 1997.

Jednu z vetvi zminene struktury trid kompaktnich prostoru tvori nasledujici tridy.

Metrizovatelne kompakty. To jsou kompaktni prostory, jejichz topologie je generovana nejakou metrikou. Tvori zakladni tridu, vsechny ostatni lze povazovat za jeji rozsireni ci zobecneni. Uvadim ji zde predevsim pro uplnost. Pro kompakt K vsechna nasledujici tvrzeni jsou ekvivalentni metrizovatelnosti.
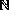- K je homeomorfni uzavrene podmnozine soucinu $[0,1]^{\Bbb N}$ , kde $\Bbb N$ znaci spocetnou mnozinu (napriklad prirozena cisla).
- K je homeomorfni (normove) kompaktni podmnozine nejakeho Banachova prostoru.
- K je homeomorfni (normove) kompaktni podmnozine nejakeho separabilniho Banachova prostoru.
- K je homeomorfni podmnozine dualu nejakeho separabilniho Banachova prostoru opatreneho slabou* topologii.
- Prostor spojitych funkci C(K) je separabilni.
Prirozene existuje mnozstvi dalsich ekvivalentnich podminek. Tyto jsem vybral, protoze ukazuji, v cem dalsi tridy zobecnuji tuto zakladni tridu. Trida metrizovatelnych kompaktu je rovnez stabilni vzhledem k ruznym operacim Konkretne je uzavrena
- na uzavrene podmnoziny
- na spojite obrazy
- spocetne souciny
- Je-li K metrizovatelny, je dualni jednotkova koule prostoru C(K), uvazovana se slabou* topologii opet metrizovatelna.
Eberleinovy kompakty. Tuto tridu tvori kompaktni prostory, ktere lze nalezt jako podmnozinu v nejakem Banachove prostoru opatrenem slabou topologii. Ukazalo se, ze uzce souvisi s tridou slabe kompaktne generovanych (weakly compactly generated, kratce WCG) prostoru, coz jsou takove Banachovy prostory, v nichz existuje slabe kompaktni podmnozina, jejiz linearni obal je husty. Nasledujici tvrzeni jsou ekvivalentni podmince, ze kompakt K je Eberleinuv.
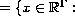
- K je homeomorfni nejake podmnozine prostoru $c_0(\Gamma)$ $=\{ x\in\Bbb R^\Gamma:$ $\forall\varepsilon>0$ $\{\gamma\in\Gamma:|x(\gamma)|\ge\varepsilon\}$ $\text{ je konecna}\}$ opatreneho slabou topologii.
- K je homeomorfni nejake podmnozine prostoru $c_0(\Gamma)$ opatreneho topologii bodove konvergence.
- K je homeomorfni nejake podmnozine nejakeho reflexivniho Banachova prostoru opatreneho slabou topologii.
- K je homeomorfni podmnozine dualu nejakeho WCG Banachova prostoru opatreneho slabou* topologii.
- Prostor spojitych funkci C(K) je WCG.
Trida Eberleinovych kompaktu je rovnez stabilni vuci operacim vyse uvedenym pro metrizovatelne kompakty.
Literatura obsahujici uvedene a pribuzne vysledky:
- D.Amir and J.Lindenstrauss, The structure of weakly compact sets in Banach spaces, Ann. Math. 88 (1968), 35-46.
- W.J.Davis, T.Figiel, W.B.Johnson and A.Pelczynski, Factoring weakly compact operators, J. Funct. Anal. 17 (1974), 311-327.
- Y.Benjamini, M.E.Rudin and M.Wage, Continuous images of weakly compact subsets of Banach spaces, Pacific J. Math. 70 (1977), 309-324.
- E.Michael and M.E.Rudin, A note on Eberlein compacts, Pacific J. Math. 72 (1977), no. 2, 487-495.
Talagrandovy a Gul'kovy kompakty. Tyto dve tridy jsou spjaty s deskriptivnimi vlastnostmi slabych topologii Banachovych prostoru. Z literatury jmenujme napriklad:
- M.Talagrand, Espaces de Banach faiblement K-analytiques, Annals of Math. 110 (1979), 403-438.
- M.Talagrand, A new countably determined Banach space, Israel J. Math. 47 (1984), 75-80.
- P.Cizek, O nekterych zobecnenich Eberleinovych kompaktu, diplomova prace, MFF UK 1996.
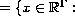
Corsonovy kompakty. Trida Corsonovych kompaktu byla puvodne zkoumana z topologickeho hlediska, az pozdeji se ukazalo, ze ma mnoho funkcionalne-analytickych vlastnosti pribuznych vlastnostem Eberleinovych kompaktu. Uvedme nejprve definici. 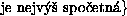Kompaktni prostor K je Corsonuv, pokud je homeomorfni nejake podmnozine prostoru $\Sigma(\Gamma)$ $=\{ x\in\Bbb R^\Gamma:$ $\{\gamma\in\Gamma:x(\gamma)\ne0\}$ $\text{ je nejvys spocetna}\}$ opatreneho topologii bodove konvergence. Nyni uvedme nektere vlastnosti Corsonovych kompaktu.
- Trida Corsonovych kompaktu je uzavrena na uzavrene podmnoziny, spocetne souciny a spojite obrazy.
- Dualni jednotkova koule prostoru C(K), opatrena slabou* topologii, je Corsonuv kompakt, prave kdyz K je takovy Corsonuv kompakt, ze kazda Radonova pravdepodobnostni mira na K ma separabilni nosic (tzv. vlasnost (M)).
- Za hypotezy kontinua existuji Corsonovy kompakty bez vlastnosti (M), a tedy prislusne dualni koule do Corsonovy tridy nepatri.
- Je-li K Corsonuv kompakt, pak prostor C(K) je Lindelofuv v topologii bodove konvergence.
Neco z literatury o Corsonovych kompaktech a pribuznych tematech:
- H.H.Corson, Normality in subsets of product spaces, Amer. J. Math. 81 (1959), 785-796.
- S.P.Gulko, Properties of sets that lie in Sigma-products, Dokl. Nauk SSSR 237 (1977), no. 3, 505-508 (rusky).
- G.Gruenhage, Covering properties of 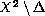$X^2\setminus\Delta$ , W-sets, and compact subsets of Sigma-products, Topol. Appl. 17 (1984), 287-304.
- M.Valdivia, Resolutions of the identity in certain Banach spaces, Collectanea Math. 39 (1988), 127-140.
- S.Argyros, S.Mercourakis and S.Negrepontis, Functional analytic properties of Corson compact spaces, Studia Math. 89 (1988), 197-229.
- J.Orihuela, W.Schachermayer and M.Valdivia, Every Radon-Nikodym Corson compact is Eberlein compact, Studia Math. 98 (1991), 157-174.
- S.Argyros and S.Mercourakis, On weakly Lindelof Banach spaces, Rocky Mountain J. Math. 23 (1993), 395-446.
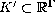Valdiviovy kompakty. Na rozdil od Corsonovych kompaktu byla trida Valdiviovych kompaktu prvotne zavedena pro potreby funkcionalni analyzy, protoze mnoho vlastnosti Corsonovych kompaktu zustava zachovano i pro tuto tridu. Az pozdeji se ukazalo, ze ma i mnozstvi zajimavych topologickych vlastnosti. Zacneme definici. Kompaktni prostor K je Valdiviuv, pokud je homeomorfni nejake mnozine , pro kterou je prunik 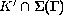husty v K'. Jednoduchym a kanonickym prikladem Valdiviova kompaktu, ktery neni Corsonuv, je ordinalni interval . Dokonce plati, ze Valdiviuv kompakt, ktery neobsahuje homeomorfni kopii , je jiz Corsonuv. Uvedme nyni nektere vlastnosti tridy Valdiviovych kompaktu, ktere jsou podstatne odlisne od vlastnosti predchozich trid.
- Valdiviovy kompakty nejsou uzavrene na uzavrene podmnoziny. Dokonce kazdy kompaktni prostor lze nalezt jako podmnozinu v nejakem Valdiviove kompaktu. To proto, ze krychle $[0,1]^\Gamma$ je Valdiviuv kompakt pro libovolnou mnozinu $\Gamma$ .
- Valdiviovy kompakty jsou uzavrene na libovolne (ne nutne spocetne) souciny.
- Valdiviovy kompakty nejsou uzavrene na spojite obrazy. Dokonce plati, ze pokud vsechny spojite obrazy nejakeho kompaktu jsou Valdiviovy, pak tento kompakt je jiz Corsonuv.
- Muze se stat, ze Banachuv prostor v jedne ekvivalentni norme ma dualni kouli Valdiviovu, a v jine nikoli. Dokonce plati, ze ma-li vuci kazde ekvivalentni norme Valdiviovu dualni kouli, pak jeho dualni koule je jiz Corsonuv kompakt.
Neco z literatury vztahujici se k Valdiviovym kompaktum:
- S.Argyros, S.Mercourakis and S.Negrepontis, Functional analytic properties of Corson compact spaces, Studia Math. 89 (1988), 197-229.
- M.Valdivia, Projective resolutions of identity in C(K) spaces, Arch. Math. 54 (1990), 493-498.
- M.Valdivia, Simultaneous resolutions of the identity operator in normed spaces, Collectanea Math. 42 (1991), no. 2, 265-284.
- R.Deville and G.Godefroy, Some applications of projective resolutions of the identity, Proc. London Math. Soc. 67 (1993), no. 1, 183-199.
- M.Valdivia, On certain compact topological spaces, Revista Matematica de la Universidad Complutense de Madrid 10 (1997), no. 1, 81-84.
- dale viz nekolik mych clanku.
Nektere z otevrenych problemu v teto oblasti:
- Je trida Valdiviovych kompaktu uzavrena na spojite otevrene obrazy? Odpoved zni ano, pokud onen obraz ma hustou mnozinu $G_\delta$ bodu. (Odpoved: NE. Protipriklad nalezli W.Kubis a V.Uspenskij.)
- Necht soucin $K\times L$ je Valdiviuv kompakt. Jsou pak K a L rovnez Valdiviovy kompakty? Odpoved je kladna, pokud aspon jeden z nich ma hustou mnozinu $G_\delta$ bodu, nebo oba maji vahy nejvyse $\aleph_1$ .
- Necht dualni jednotkova koule Banachova prostoru je Valdiviuv kompakt (ve slabe* topologii). Existuje pak jeji "valdiviovske" vnoreni do $\Bbb R^\Gamma$ , ktere je navic linearni? (Odpoved: NE)
- Necht dualni jednotkova koule prostoru C(K) je Valdiviuv kompakt. Je pak K take Valdiviuv? (Ano, pokud K ma hustou mnozinu $G_\delta$ bodu.) (Odpoved: NE. Protipriklad nalezli T.Banakh a W.Kubis.)
- Necht X je Banachuv prostor takovy, ze dualni jednotkova koule kazdeho jeho podprostoru je Valdiviuv kompakt. Je pak dualni jednotkova koule prostoru X Corsonuv kompakt?
CESKY - ISO 8859