Contents
Question 2
We study the ordinary differential equation:

function q2_solution
a) Analysis of Steady States
We first study the steady state 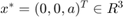 analytically:
analytically:
We first calculate the jacobian (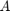 ) at
) at 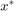 :
:
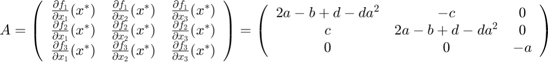
We now calculate the spectrum 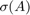 using
using
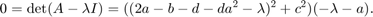
From this we get that 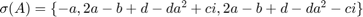 .
.
The steady state is A-stable if the maximum of the real parts of the eigenvalue is negative; i.e.,
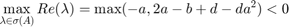
We consider for  ,
, 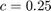 ,
, 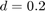 and all values of
and all values of  ; then,
; then,
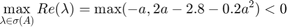
We get that 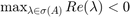 when
when 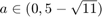 or
or 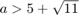 .
.
Now we study numerically for  ,
,  ,
, 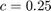 ,
, 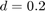 .
.
b = 3; c = 0.25; d = 0.2; disp('--------------------------------------------------'); steady_state(1.0,b,c,d); disp('--------------------------------------------------'); steady_state(1.95,b,c,d); disp('--------------------------------------------------'); steady_state(2.02,b,c,d); disp('--------------------------------------------------');
--------------------------------------------------
(a,b,c,d) = (1.000000,3.000000,0.250000,0.200000)
Jacobian:
-1.000000000000000 -0.250000000000000 0
0.250000000000000 -1.000000000000000 0
0 0 -1.000000000000000
Eigenvalues:
-1.000000000000000 + 0.250000000000000i
-1.000000000000000 - 0.250000000000000i
-1.000000000000000 + 0.000000000000000i
Maximum of real part of eigenvalues: -1.000000
Steady state is A-stable
--------------------------------------------------
(a,b,c,d) = (1.950000,3.000000,0.250000,0.200000)
Jacobian:
0.339500000000000 -0.250000000000000 0
0.250000000000000 0.339500000000000 0
0 0 -1.950000000000000
Eigenvalues:
0.339500000000000 + 0.250000000000000i
0.339500000000000 - 0.250000000000000i
-1.950000000000000 + 0.000000000000000i
Maximum of real part of eigenvalues: 0.339500
Steady state is NOT A-stable
--------------------------------------------------
(a,b,c,d) = (2.020000,3.000000,0.250000,0.200000)
Jacobian:
0.423920000000000 -0.250000000000000 0
0.250000000000000 0.423920000000000 0
0 0 -2.020000000000000
Eigenvalues:
0.423920000000000 + 0.250000000000000i
0.423920000000000 - 0.250000000000000i
-2.020000000000000 + 0.000000000000000i
Maximum of real part of eigenvalues: 0.423920
Steady state is NOT A-stable
--------------------------------------------------
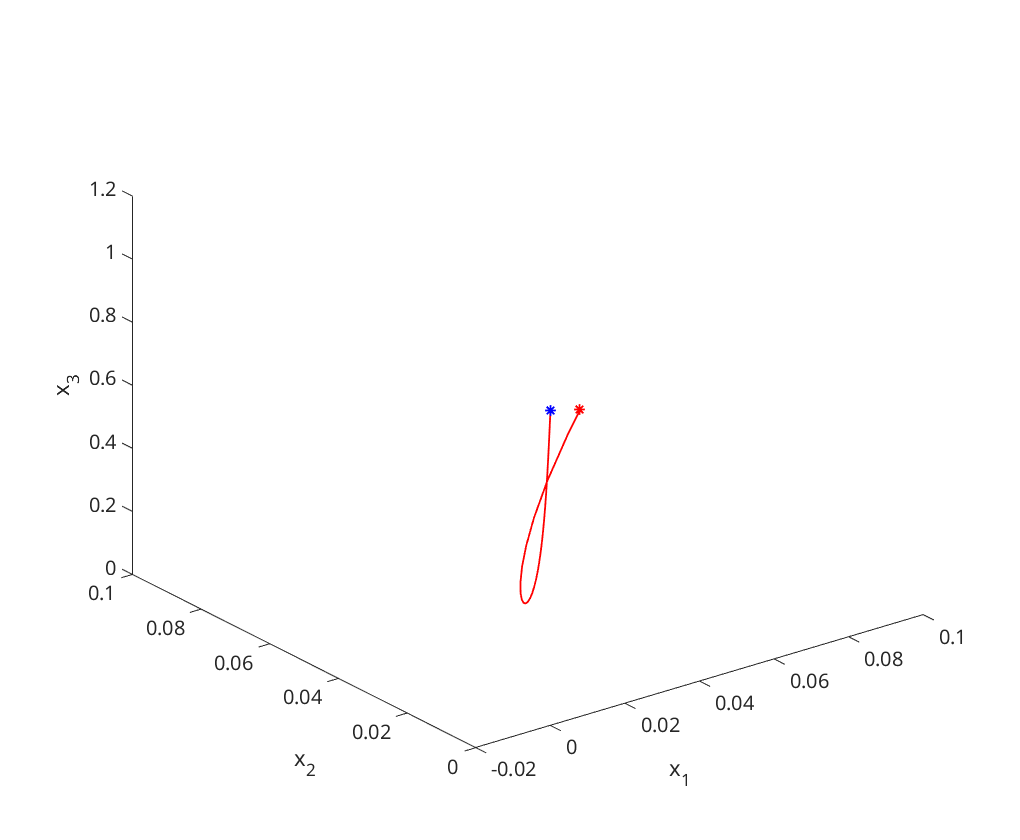
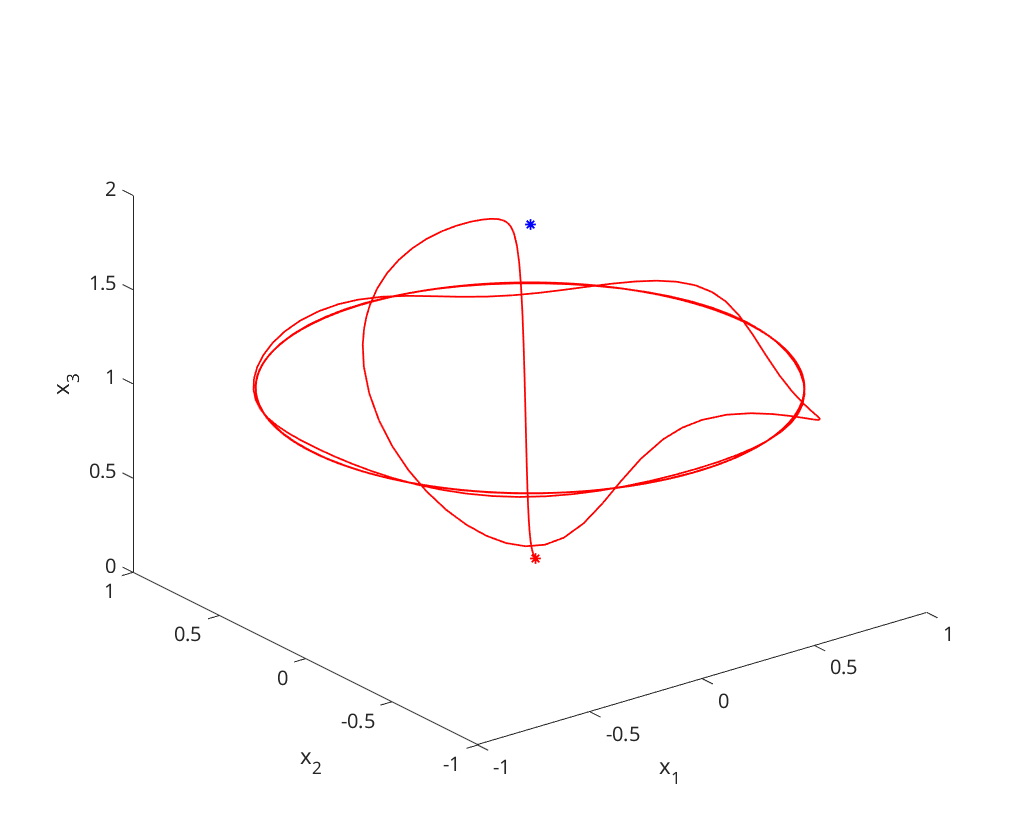
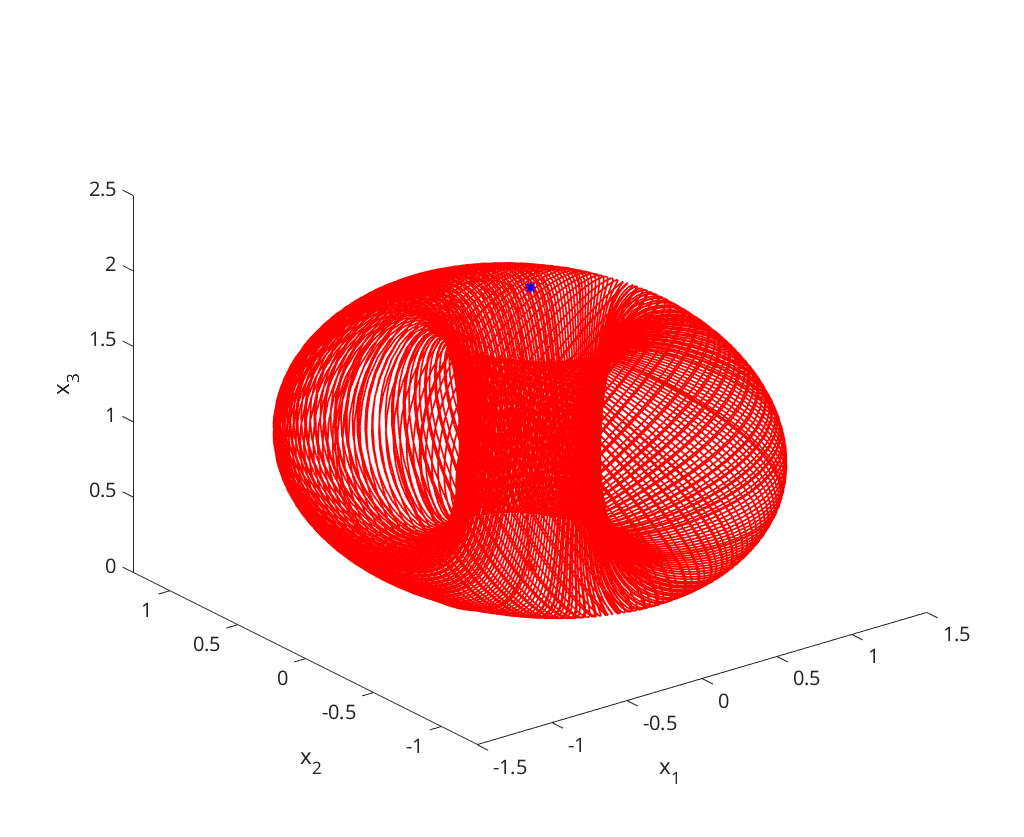
b)  -limit
-limit
omega_limit(1.0,b,c,d); omega_limit(1.95,b,c,d); omega_limit(2.02,b,c,d);
Utility function for analysis of Steady State 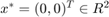
function steady_state(a,b,c,d) fprintf('(a,b,c,d) = (%f,%f,%f,%f)\n\n', a,b,c,d); % Jacobian at steady state: A = [2*a-b+d*(1-a^2), -c, 0; c, 2*a-b+d*(1-a^2), 0; 0, 0, -a]; disp('Jacobian:'); disp(A); % Eigenvalues: ev = eig(A); disp('Eigenvalues:'); disp(ev); % A-stable?: fprintf('Maximum of real part of eigenvalues: %f\n\n', max(real(ev))); if max(real(ev)) < 0 disp('Steady state is A-stable') else disp('Steady state is NOT A-stable') end end
Utility function to estimate  -limit
-limit
function omega_limit(a,b,c,d) figure; f = @(t,x)[ (a-b)*x(1)-c*x(2)+x(1)*(x(3)+d*(1-x(3)^2)); ... c*x(1)+(a-b)*x(2)+x(2)*(x(3)+d*(1-x(3)^2)); ... a*x(3)-(x(1)^2+x(2)^2+x(3)^2) ]; x0 = [.1;.1;.1]; xstar = [0;0;a]; plot3(x0(1),x0(2),x0(3),'r*'); hold on; plot3(xstar(1),xstar(2),xstar(3),'b*'); [~,x]=ode23s(f, [0,2000], x0); plot3(x(:,1),x(:,2),x(:,3),'r'); xlabel('x_1'); ylabel('x_2'); zlabel('x_3'); end
end