Contents
Question 1
We consider Van der Pol's oscillator:
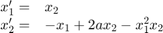
function q1_solution
a) Backwards & Forwards solve with ode23s
 ; Initial condition
; Initial condition 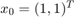
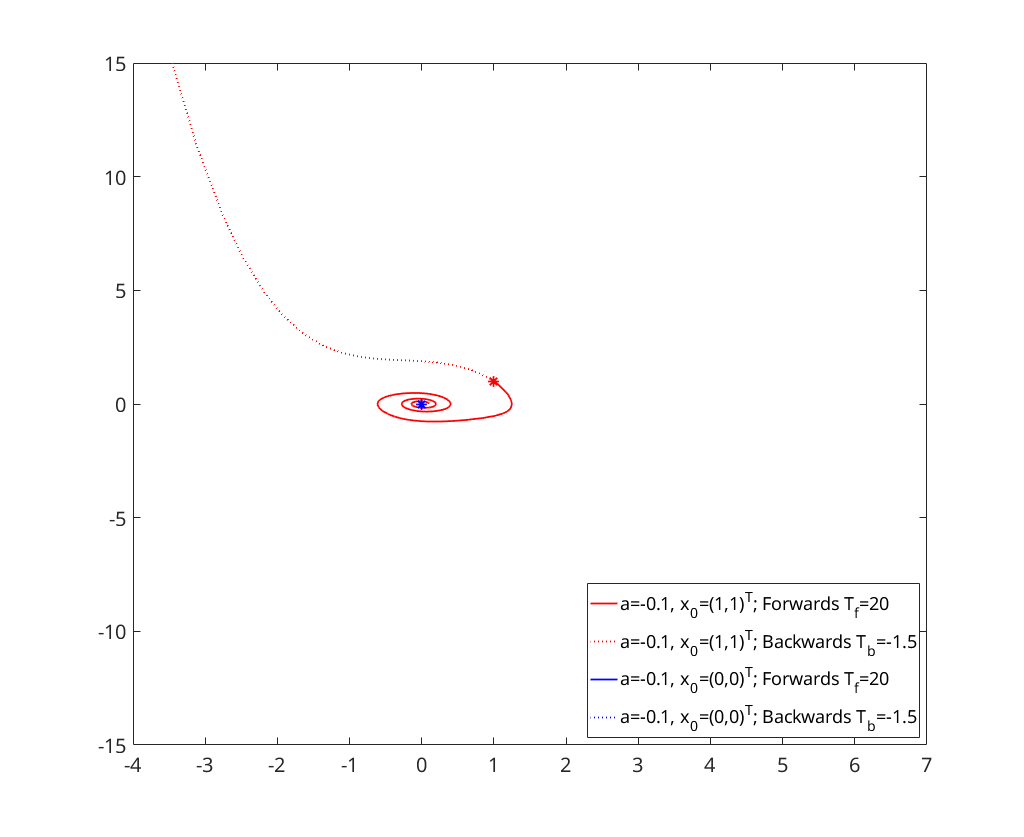
a = -0.1; x0 = [1;1]; % Plot initial point plot(x0(1),x0(2),'r*','HandleVisibility','off'); hold on; xlim([-4 7]); ylim([-15, 15]); % Solve forward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,20], x0); plot(x(:,1),x(:,2),'r','DisplayName','a=-0.1, x_0=(1,1)^T; Forwards T_f=20'); % Solve backward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,-1.8], x0); plot(x(:,1),x(:,2),':r','DisplayName','a=-0.1, x_0=(1,1)^T; Backwards T_b=-1.5');
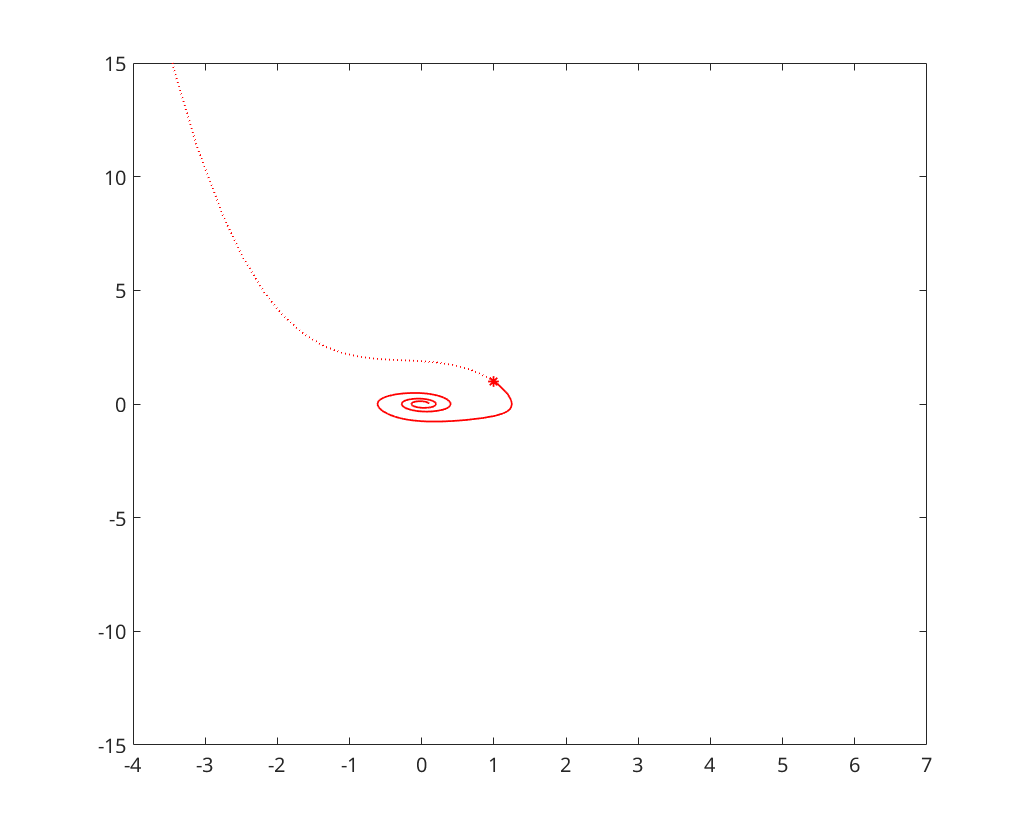
 ; Initial condition
; Initial condition 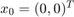
a = -0.1; x0 = [0;0]; % Plot initial point plot(x0(1),x0(2),'b*','HandleVisibility','off'); hold on; legend('Location','SouthEast'); % Solve forward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,20], x0); plot(x(:,1),x(:,2),'b','DisplayName','a=-0.1, x_0=(0,0)^T; Forwards T_f=20'); % Solve backward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,-1.5], x0); plot(x(:,1),x(:,2),':b','DisplayName','a=-0.1, x_0=(0,0)^T; Backwards T_b=-1.5');
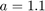 ; Initial condition
; Initial condition 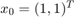
a = 1.1; x0 = [1;1]; % Plot initial point plot(x0(1),x0(2),'m*','HandleVisibility','off'); hold on; % Solve forward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,20], x0); plot(x(:,1),x(:,2),'m','DisplayName','a=1.1, x_0=(1,1)^T; Forwards T_f=20'); % Solve backward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,-1.5], x0); plot(x(:,1),x(:,2),':m','DisplayName','a=1.1, x_0=(1,1)^T; Backwards T_b=-1.5');
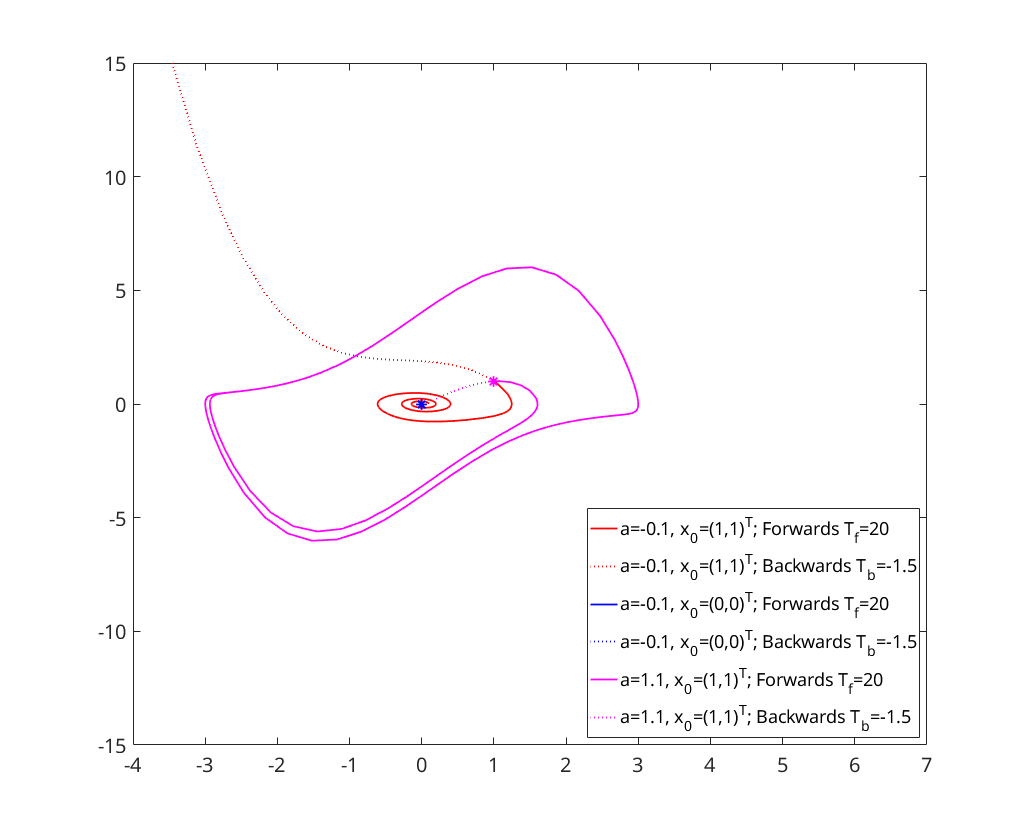
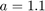 ; Initial condition
; Initial condition 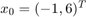
a = 1.1; x0 = [-1;6]; % Plot initial point plot(x0(1),x0(2),'k*','HandleVisibility','off'); hold on; % Solve forward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,20], x0); plot(x(:,1),x(:,2),'k','DisplayName','a=1.1, x_0=(-1,6)^T; Forwards T_f=20'); % Solve backward [~,x]=ode23s(@(t,x)vdpol(t,x,a), [0,-0.4], x0); plot(x(:,1),x(:,2),':k','DisplayName','a=1.1, x_0=(-1,6)^T; Backwards T_b=-0.4');
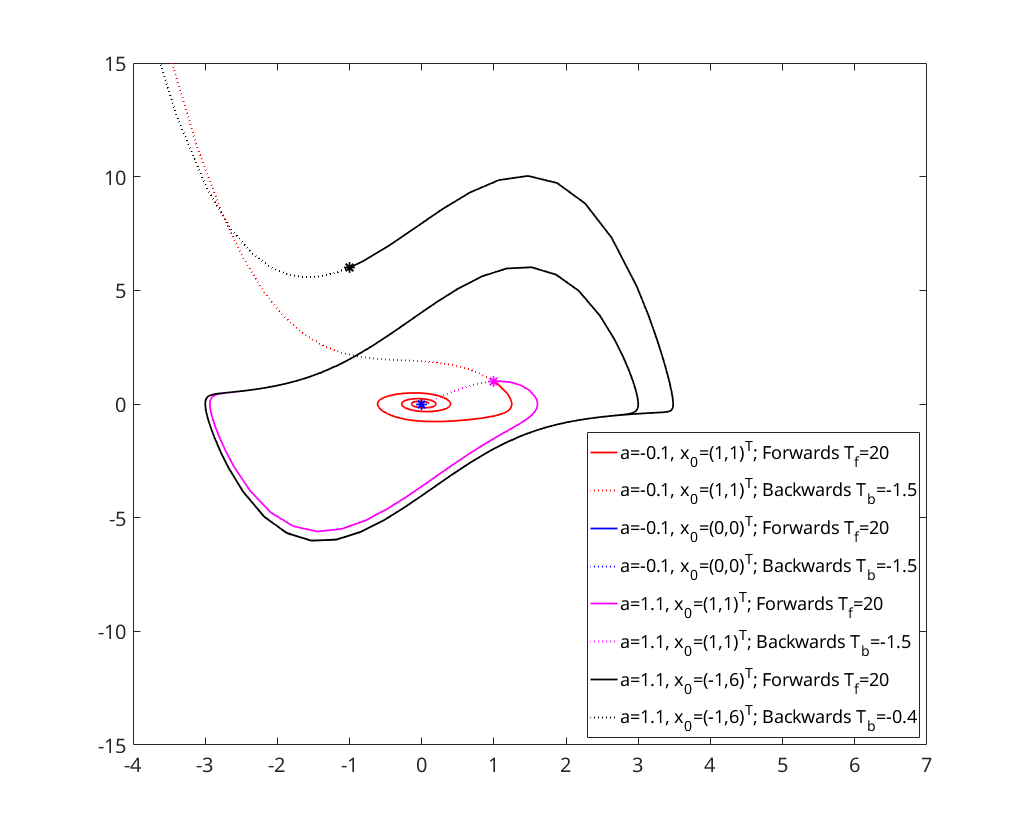
b) Analysis of Steady States
We now study the steady state 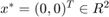 for
for 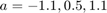
disp('----------------------------------------'); vdpol_steady(-1.1); disp('----------------------------------------'); vdpol_steady(0.5); disp('----------------------------------------'); vdpol_steady(1.1); disp('----------------------------------------');
----------------------------------------
a = -1.100000
Jacobian:
0 1.000000000000000
-1.000000000000000 -2.200000000000000
Eigenvalues:
-0.641742430504416
-1.558257569495584
Maximum of real part of eigenvalues: -0.641742
Steady state is A-stable
----------------------------------------
a = 0.500000
Jacobian:
0 1
-1 1
Eigenvalues:
0.500000000000000 + 0.866025403784438i
0.500000000000000 - 0.866025403784438i
Maximum of real part of eigenvalues: 0.500000
Steady state is NOT A-stable
----------------------------------------
a = 1.100000
Jacobian:
0 1.000000000000000
-1.000000000000000 2.200000000000000
Eigenvalues:
0.641742430504416
1.558257569495584
Maximum of real part of eigenvalues: 1.558258
Steady state is NOT A-stable
----------------------------------------
c) Numerical approximation
We calculate the numerical approximation for initial condition 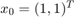 and
and 
We start using Euler with 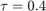 and notice that the solution does not converge to the steady state, instead getting stuck in an orbit around the steady state as the the fixed point of the Euler method with
and notice that the solution does not converge to the steady state, instead getting stuck in an orbit around the steady state as the the fixed point of the Euler method with 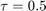 is NOT
is NOT  -stable
-stable
figure; a = -0.1; x0 = [1;1]; [~,x]=eul(@(t,x)vdpol(t,x,a), 0, 120, x0, 0.4); plot(x(:,1),x(:,2));
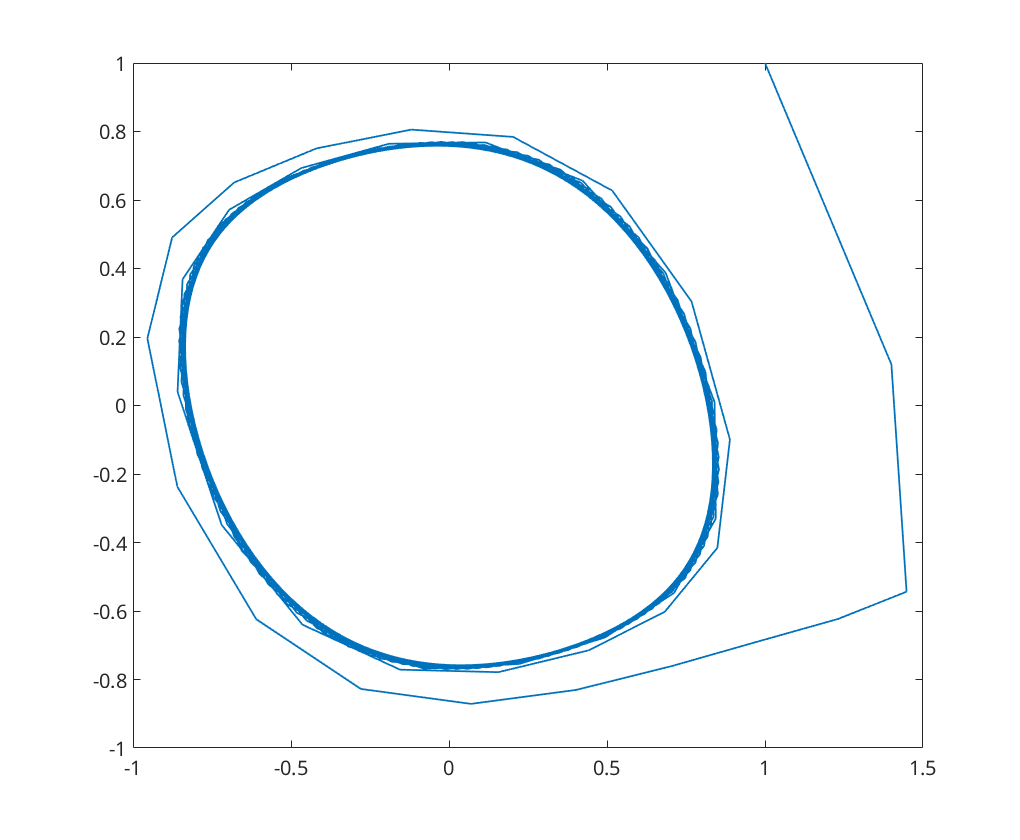
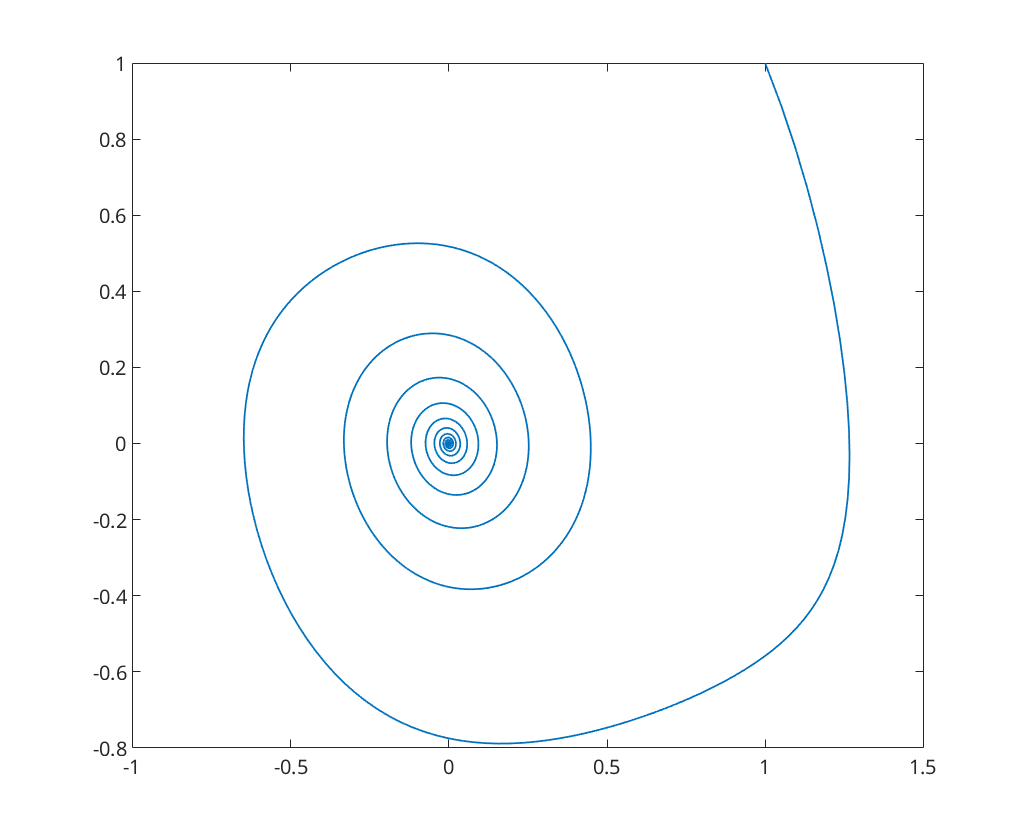
Decreasing the time step size to 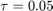 the fixed point is now
the fixed point is now 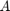 -stable
-stable
figure; a = -0.1; x0 = [1;1]; [~,x]=eul(@(t,x)vdpol(t,x,a), 0, 120, x0, 0.05); plot(x(:,1),x(:,2));
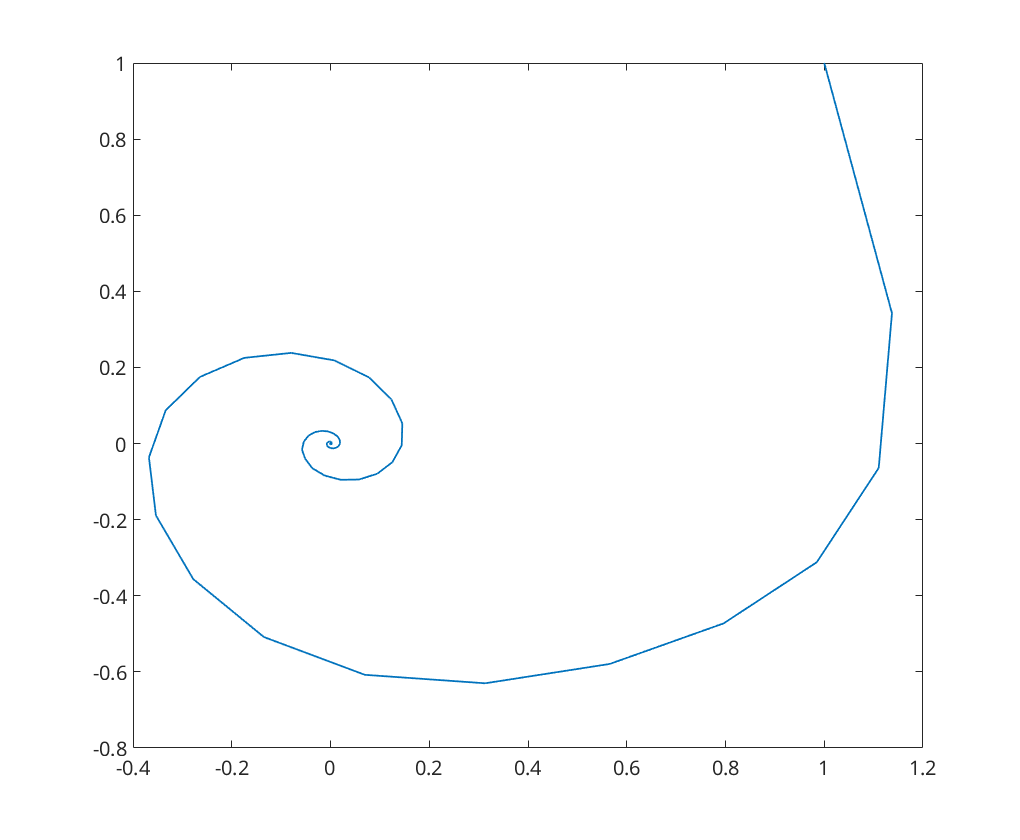
For implicit Euler, the fixed point is 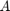 -stable even with
-stable even with 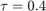
figure; a = -0.1; x0 = [1;1]; [~,x]=ieuler(@(t,x)vdpol(t,x,a), 0, 120, x0, 0.4); plot(x(:,1),x(:,2));
Utility function for analysis of Steady State 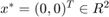
function vdpol_steady(a) fprintf('a = %f\n\n', a); % Jacobian at steady state: A = [0 1; -1 2*a]; disp('Jacobian:'); disp(A); % Eigenvalues: ev = eig(A); disp('Eigenvalues:'); disp(ev); % A-stable?: fprintf('Maximum of real part of eigenvalues: %f\n\n', max(real(ev))); if max(real(ev)) < 0 disp('Steady state is A-stable') else disp('Steady state is NOT A-stable') end end
end