Q3 Solution

Contents

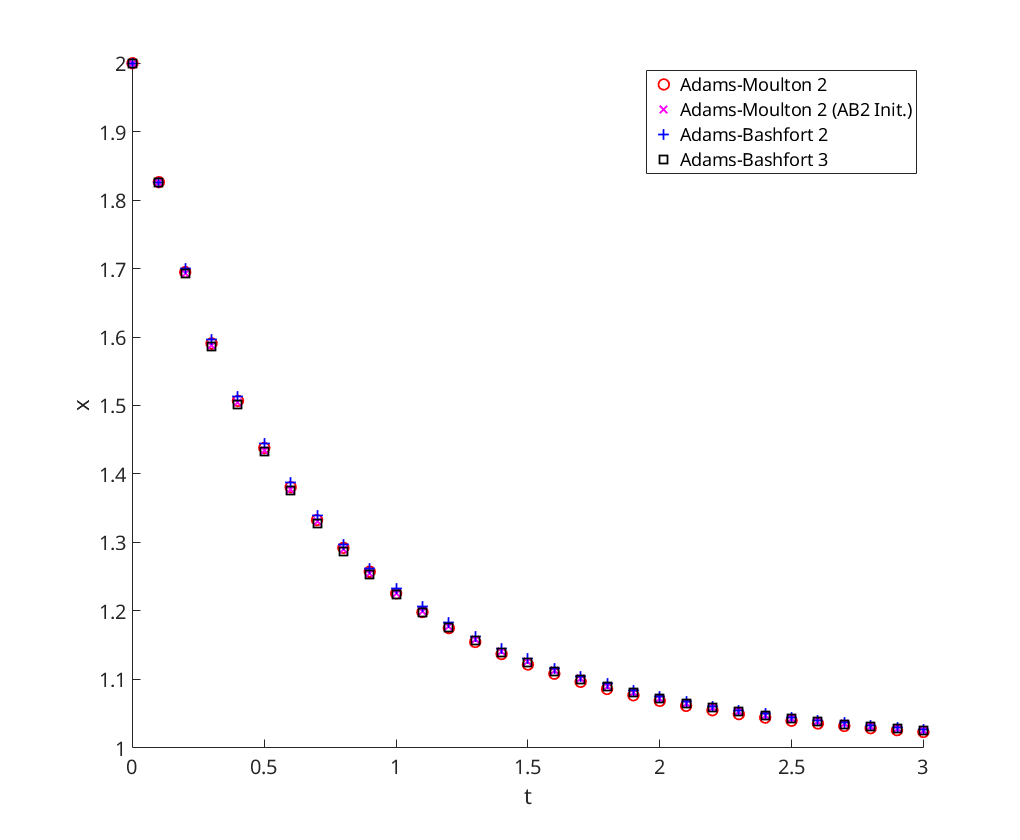
a) Logistic Method - Adams-Moulton 2-step

We solve the logistic problem

$x'=(1-x)x, x(0)=2$

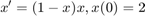
using Adams-Moulton 2, Adams-Moulton 2 with AB2 initial guess, Adams-Bashfort 2, and Adams-Bashfort 3

function q3_solution

figure;
axis([0 3 1 2]);
hold on;
xlabel('t');
ylabel('x');
[t,x]=am2(@logistic,0,3, 2, .1);
plot(t,x(:,1),'ro','DisplayName','Adams-Moulton 2');

[t,x]=am2_mod(@logistic,0,3, 2, .1);
plot(t,x(:,1),'mx','DisplayName','Adams-Moulton 2 (AB2 Init.)');

[t,x]=ab2(@logistic,0,3, 2, .1);
plot(t,x(:,1),'b+','DisplayName','Adams-Bashfort 2');

[t,x]=ab3(@logistic,0,3, 2, .1);
plot(t,x(:,1),'ks','DisplayName','Adams-Bashfort 3');

legend('Location', 'NorthEast');

b) Linear Oscillator - Adams-Moulton 2-step

We solve linear oscillator with 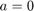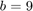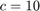$a = 0$, $b = 9$, $c = 10$, $\omega = 1$ and $x_0=(2,1)^T$ using Adams-Moulton 2, Adams-Moulton 2 with AB2 initial guess, Adams-Bashfort 2, and Adams-Bashfort 3

figure
axis([0 10 -4 4]);
hold on;
xlabel('x_1');
ylabel('x_2');

[t,x]=am2(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'ro','DisplayName','Adams-Moulton 2');

[t,x]=am2_mod(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'mx','DisplayName','Adams-Moulton 2 (AB2 Init.)');

[t,x]=ab2(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'b+','DisplayName','Adams-Bashfort 2');

[t,x]=ab3(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'ks','DisplayName','Adams-Bashfort 3');

legend('Location', 'NorthEast');

c) Linear System - Adams-Moulton 2-step

We solve the stiff linear system with 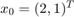$x_0=(2,1)^T$ using Adams-Moulton 2, Adams-Moulton 2 with AB2 initial guess, Adams-Bashfort 2, and Adams-Bashfort 3

figure
axis([0 10 -4 4]);
hold on;
xlabel('x_1');
ylabel('x_2');

[t,x]=am2(@linsystem,0,.1, [2;1], .001);
plot(t,x(:,1),'ro','DisplayName','Adams-Moulton 2');

[t,x]=am2_mod(@linsystem,0,.1, [2;1], .001);
plot(t,x(:,1),'mx','DisplayName','Adams-Moulton 2 (AB2 Init.)');

[t,x]=ab2(@linsystem,0,.1, [2;1], .001);
plot(t,x(:,1),'b+','DisplayName','Adams-Bashfort 2');

[t,x]=ab3(@linsystem,0,.1, [2;1], .001);
plot(t,x(:,1),'ks','DisplayName','Adams-Bashfort 3');

ylim([-5 15]);
xlim([0 .12]);
legend('Location', 'NorthEast');

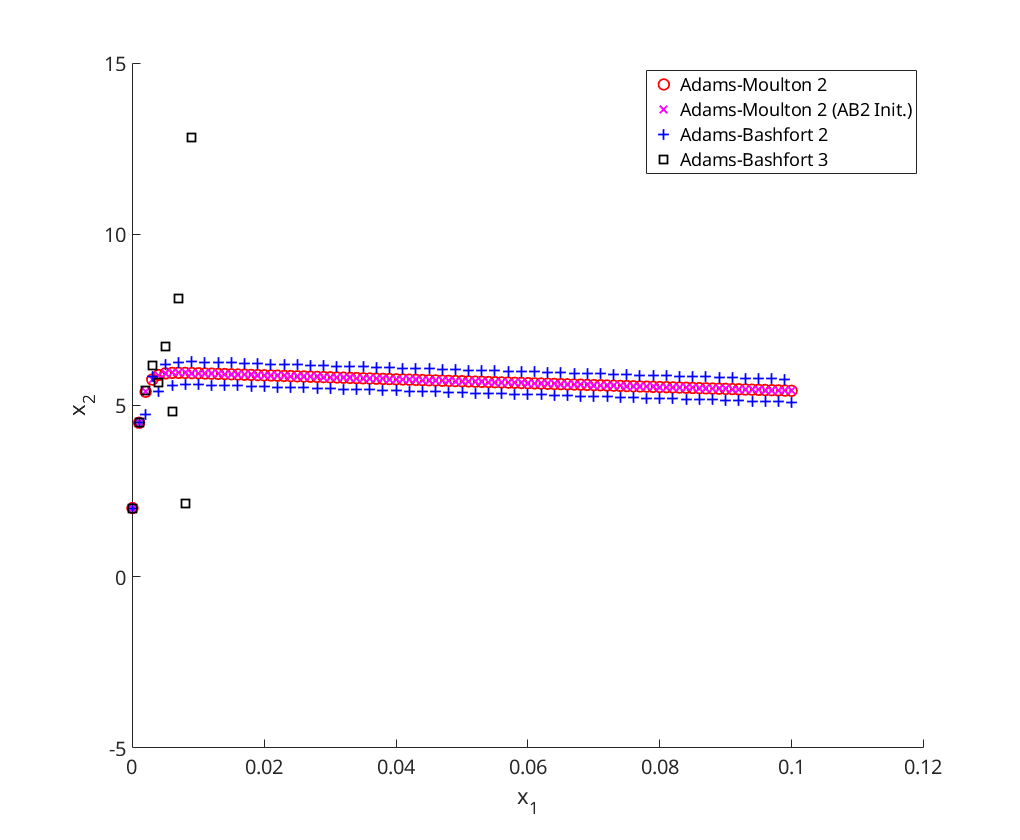
Convergence Analysis for Adams-Moulton

We perform convergence analysis for 2-step Adams-Moulton

fprintf('Adams-Moulton 2-step             = ');
conv_analysis(@am2);
fprintf('Adams-Moulton 2-step (AB2 Init.) = ');
conv_analysis(@am2_mod);

Adams-Moulton 2-step             = log_{10}E_N = -1.757798 + 0.685327 x log10(h)
Adams-Moulton 2-step (AB2 Init.) = log_{10}E_N = -1.377970 + 2.807129 x log10(h)

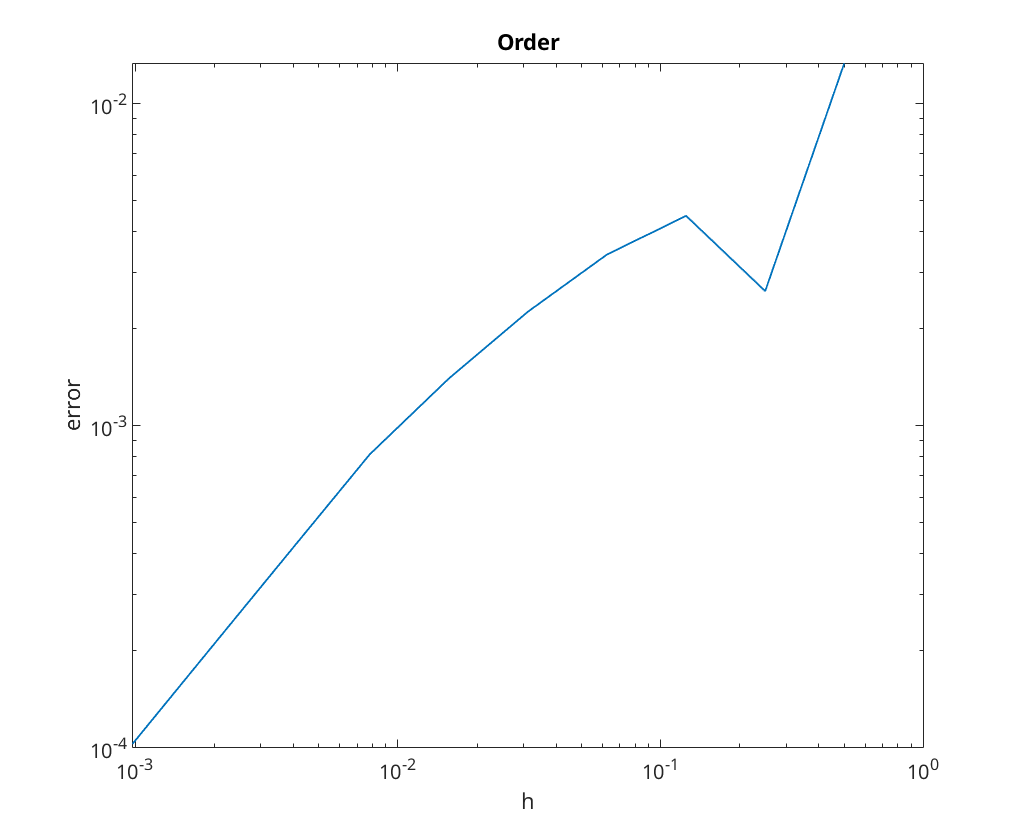
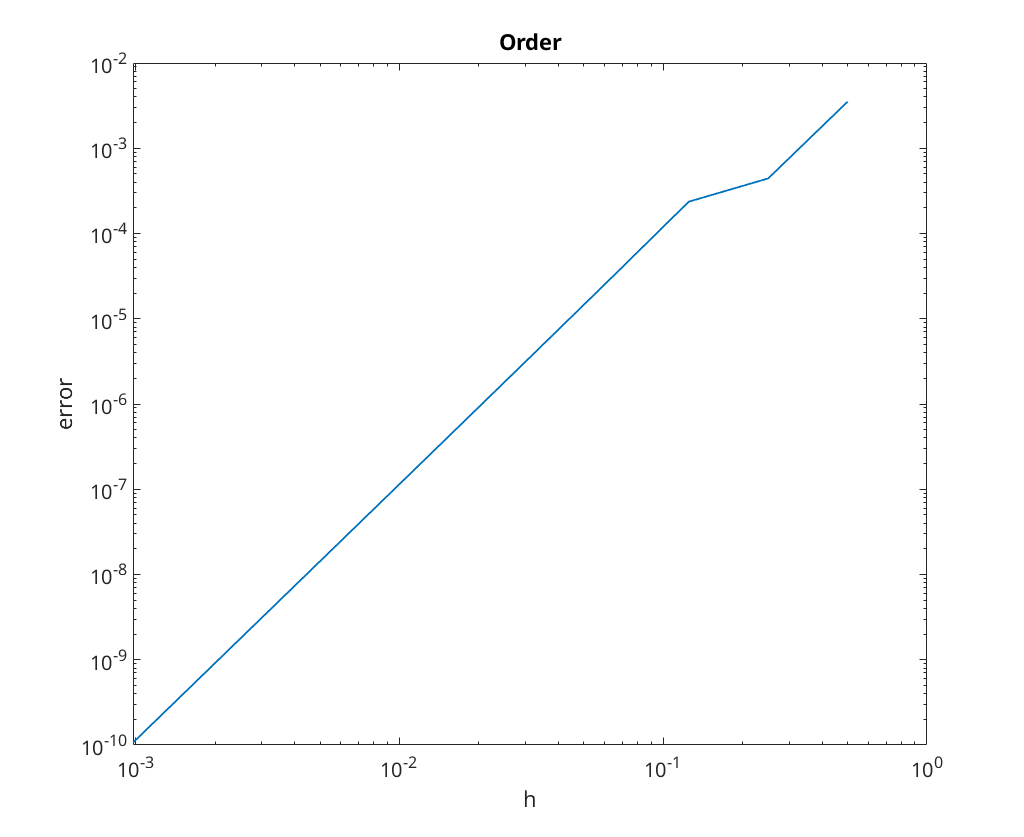
We perform convergence analysis for 2-step Adams-Moulton with various tolerances (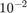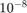$10^{-2}$, ..., $10^{-8}$) for the fixed point iteration

Note: the following uses a modified version of conv_analysis which suppresses the output. This is purely for simplicity of the published output, so can be replaced by the normal conv_analysis

conv = zeros(7,2);
conv(:,1) = 10.^(-2:-1:-8);
figure;
for i=1:size(conv,1)
    conv(i,2) = conv_analysis(@(field, t0, T, x0, h)...
        am2_tol(field, t0, T, x0, h, conv(i,1)), Output=0, NewFigure=0);
    hold on;
end
legend('tol=10^{-2}','tol=10^{-3}','tol=10^{-4}','tol=10^{-5}',...
    'tol=10^{-6}','tol=10^{-7}','tol=10^{-7}',Location='SouthEast');
disp(array2table(conv,VariableNames={'Tolerance','Order of Convergence'}));

    Tolerance    Order of Convergence
    _________    ____________________

       0.01       0.514871250816776  
      0.001          0.561782413353  
     0.0001        1.35813085476437  
      1e-05        1.77360613967155  
      1e-06        2.05729238060897  
      1e-07        2.67281067051432  
      1e-08        3.08911231844274  

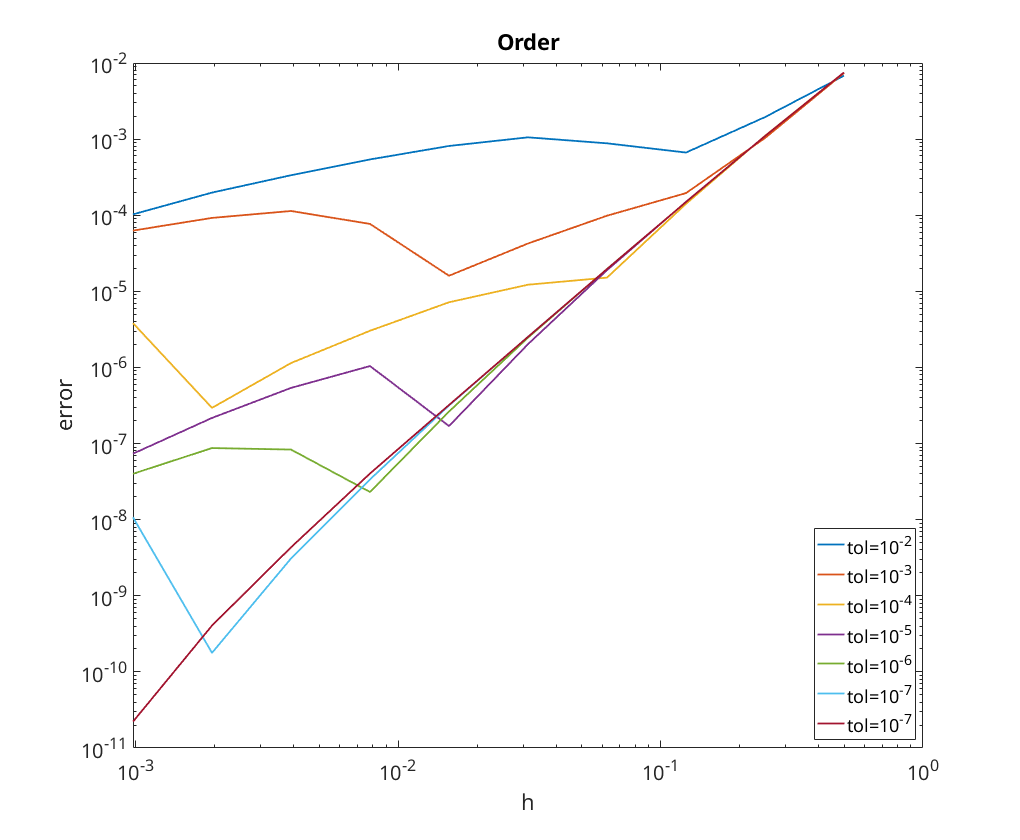
We notice that if the tolerance is too large it limits the rate of convergence due to the fact that as the step size decreases the convergence is limited by the tolerance as opposed to step size

end

Modified Adams-Moulton 2 to support passing tolerance as an argument

function [t,x] = am2_tol(field, t0, T, x0, h, tol)

m = 2;
n = ceil((T-t0)/h);

t = t0+h*(0:n).';
x = ones(n+1,length(x0));
[t(1:m), x(1:m,:)] = rk_classical(field, t0, t0+(m-1)*h, x0, h);

f0 = feval(field, t(m), x(m,:)');
f1 = feval(field, t(m-1), x(m-1,:).');
for i=m:n
    f_old = feval(field, t(i)+h, x(i,:).');
    x(i+1,:) = x(i,:).' + h*(5*f_old+8*f0-f1)/12;
    f_new = feval(field, t(i)+h, x(i+1,:).');
    while norm(f_old-f_new, 'inf') >= tol
        f_old = f_new;
        x(i+1,:) = x(i,:).' + h*(5*f_old+8*f0-f1)/12;
        f_new = feval(field, t(i)+h, x(i+1,:).');
    end
    f1 = f0;
    f0 = f_new;
end

end

Published with MATLAB® R2023a