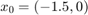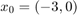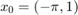Question 1(b) - Pendulum

Comparison of Euler, Runge, and Runge-Kutta for 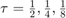$\tau=\frac12,\frac14,\frac18$ to ode23

Contents

Initial Setup

k=1;
pendulum = @(t,x)[x(2); -k*sin(x(1))];
t0 = 0;
T = 6*pi;

$x_0=(-1.5, 0)$

x0 = [-1.5 0];
[t,x]=ode23(pendulum, [t0, T], x0);
fig = figure;
plot(t,x(:,1),'-k','DisplayName','ode23');
hold on;

xlabel('time');
ylabel('x');
[t,x]=eul(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-ro','DisplayName','Euler (\tau=1/2)');
[t,x]=eul(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-rx','DisplayName','Euler (\tau=1/4)');
[t,x]=eul(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-r+','DisplayName','Euler (\tau=1/8)');
[t,x]=runge(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-bo','DisplayName','Runge (\tau=1/2)');
[t,x]=runge(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-bx','DisplayName','Runge (\tau=1/4)');
[t,x]=runge(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-b+','DisplayName','Runge (\tau=1/8)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-mo','DisplayName','Runge-Kutta (\tau=1/2)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-mx','DisplayName','Runge-Kutta (\tau=1/4)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-m+','DisplayName','Runge-Kutta (\tau=1/8)');
legend('Location','NorthEastOutside');
ylim([-5, 5]);

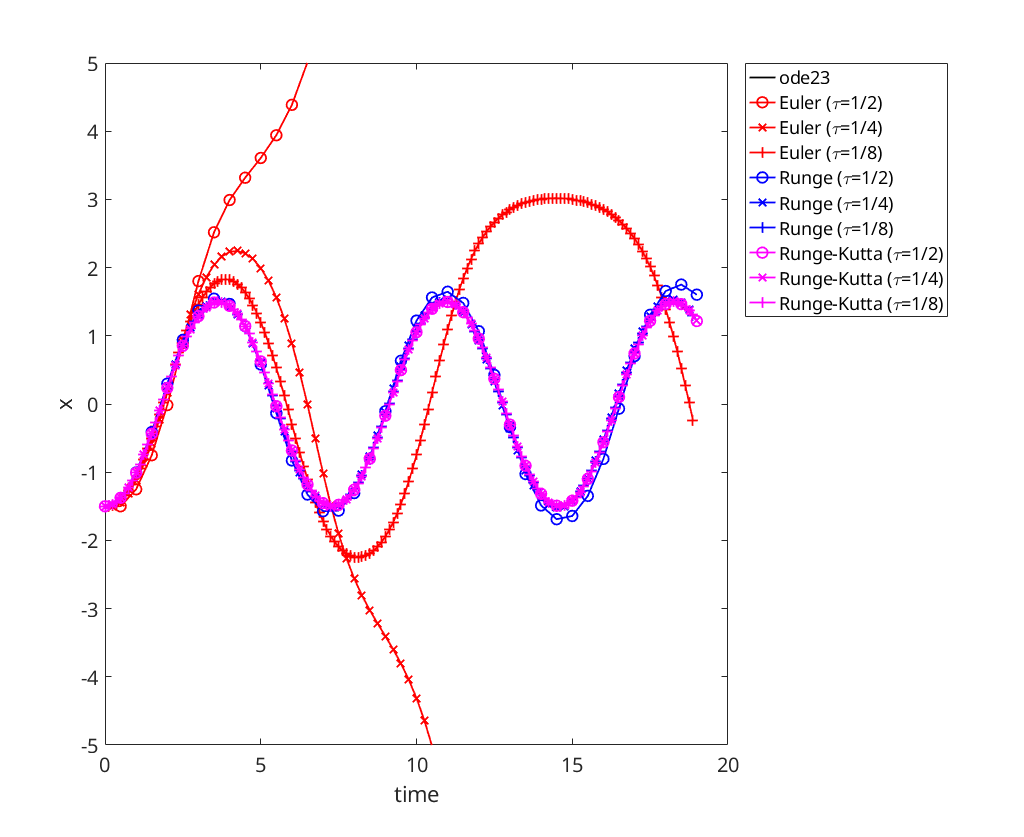
Due to the oscillations in the solution Euler (especially for low $\tau$) quickly diverges from the solution. Runge is better, but towards the end it is still slightly divergent; whereas, Runge-Kutta seems good for all $\tau$.

$x_0=(-3, 0)$

x0 = [-3 0];
[t,x]=ode23(pendulum, [t0, T], x0);
fig = figure;
plot(t,x(:,1),'-k','DisplayName','ode23');
hold on;

xlabel('time');
ylabel('x');
[t,x]=eul(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-ro','DisplayName','Euler (\tau=1/2)');
[t,x]=eul(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-rx','DisplayName','Euler (\tau=1/4)');
[t,x]=eul(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-r+','DisplayName','Euler (\tau=1/8)');
[t,x]=runge(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-bo','DisplayName','Runge (\tau=1/2)');
[t,x]=runge(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-bx','DisplayName','Runge (\tau=1/4)');
[t,x]=runge(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-b+','DisplayName','Runge (\tau=1/8)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-mo','DisplayName','Runge-Kutta (\tau=1/2)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-mx','DisplayName','Runge-Kutta (\tau=1/4)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-m+','DisplayName','Runge-Kutta (\tau=1/8)');
legend('Location','NorthEastOutside');
ylim([-5, 5]);

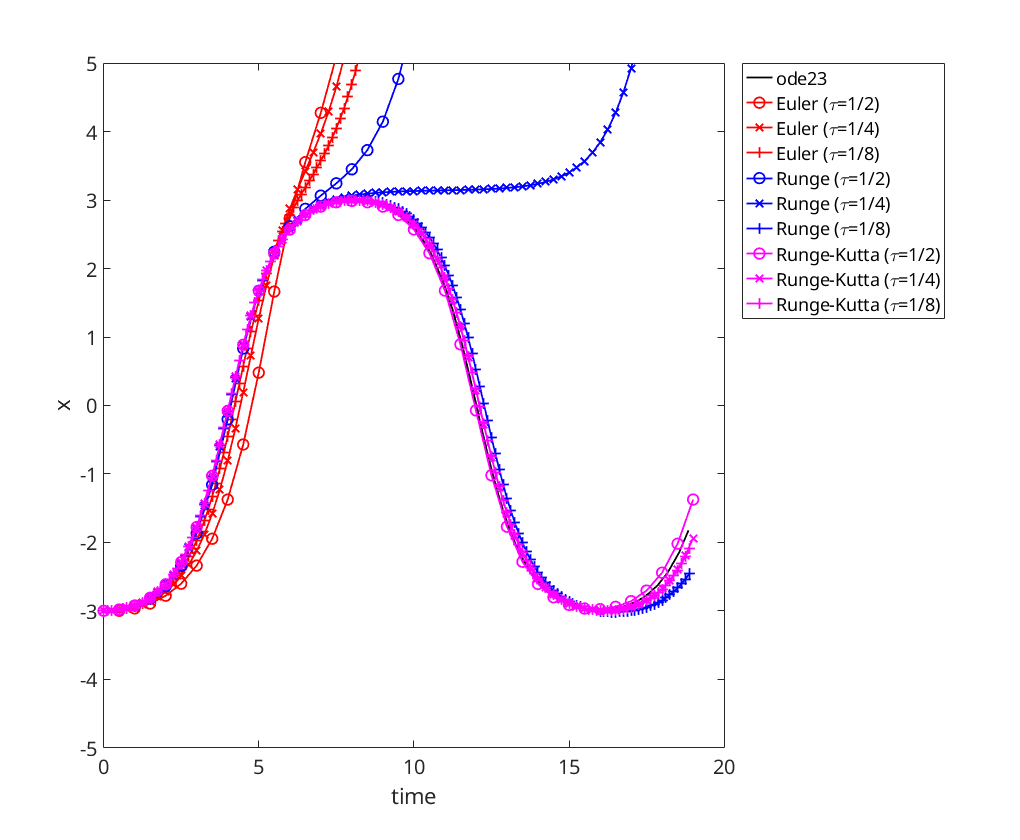
Runge is now also diverging from the solution, and even Runge-Kutta has some error.

$x_0=(-\pi, 1)$

x0 = [-pi 1];
[t,x]=ode23(pendulum, [t0, T], x0);
fig = figure;
plot(t,x(:,1),'-k','DisplayName','ode23');
hold on;

xlabel('time');
ylabel('x');
[t,x]=eul(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-ro','DisplayName','Euler (\tau=1/2)');
[t,x]=eul(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-rx','DisplayName','Euler (\tau=1/4)');
[t,x]=eul(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-r+','DisplayName','Euler (\tau=1/8)');
[t,x]=runge(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-bo','DisplayName','Runge (\tau=1/2)');
[t,x]=runge(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-bx','DisplayName','Runge (\tau=1/4)');
[t,x]=runge(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-b+','DisplayName','Runge (\tau=1/8)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/2); plot(t,x(:,1),'-mo','DisplayName','Runge-Kutta (\tau=1/2)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/4); plot(t,x(:,1),'-mx','DisplayName','Runge-Kutta (\tau=1/4)');
[t,x]=rk_classical(pendulum, t0, T, x0, 1/8); plot(t,x(:,1),'-m+','DisplayName','Runge-Kutta (\tau=1/8)');
legend('Location','NorthEastOutside');
ylim([-5, 5]);

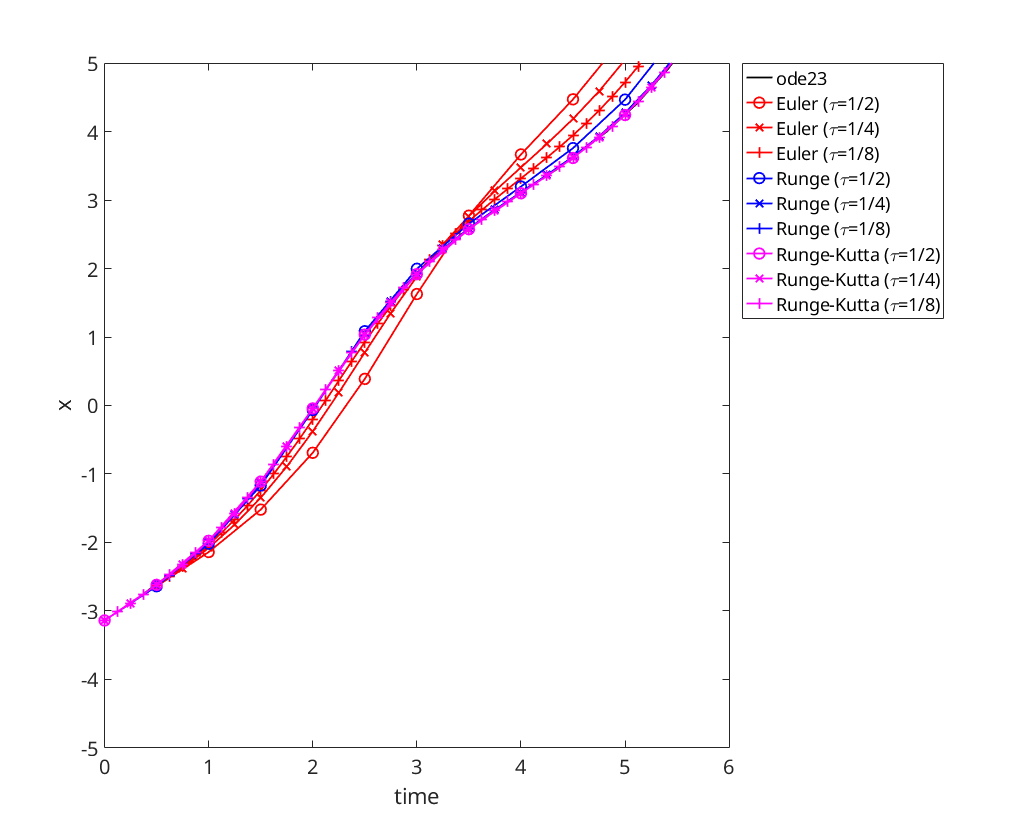
All solutions are fairly good.

Published with MATLAB® R2023a