Cvičení X
Nechť $m$, $n$ jsou nesoudělná přirozená čísla a označme $\NN$ podgrupu sčítací grupy $\Z \times \Z$ generovanou dvojicí $(m, n)$. Dokažte, že $(\Z \times \Z)/\NN$ je isomorfní $\Z$.
Nápověda
Vyrobte homomorfismus do $\Z$, který bude mít $\NN$ jako jádro.
Řešení
Definujme $f \colon \Z \times \Z \to \Z$ předpisem $f(x,y) = nx - my$. Jelikož jsou $m$ a $n$ nesoudělná, z Bézoutovy věty nalezneme $x, y \in \Z$ taková, že $f(x,y) = 1$, takže obrazem $f$ je celé $\Z$. Na druhou stranu, je-li $(x, y) \in \Ker f$, pak $nx - my = 0$, což lze (pro nenulová $x$, $y$) přepsat jako
\[ \frac xy = \frac mn. \]
Jelikož jsou $m$ a $n$ nesoudělná, je zlomek na pravé straně v základním tvaru, takže $(x, y)$ musí být násobkem $(m, n)$. Jinak řečeno, $\Ker f$ je přesně podgrupa generovaná $(m, n)$. První věta o isomorfismu dává požadovaný isomorfismus.
(Na tuto úlohu jsem hrdý 🙂)
-
Dokažte, že grupa $\G$ takových permutací bodů $A, \dots, G$, které zachovají kolinearitu ve Fanově rovině
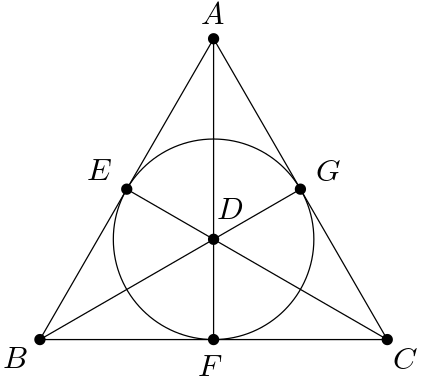
(tj. pokud tři body leží na „přímce“ (tj. přímce nebo kružnici), budou na „přímce“ ležet i jejich obrazy), je isomorfní $\GL_3(\Z_2)$.
- Jakým permutacím v $\G$ odpovídají elementární matice? Vyvoďte, že všechny permutace v $\G$ jsou sudé.
- Kolik má $\GL_3(\Z_2)$ prvků (tj. jaký má řád)?
- Ukažte, že v $\GL_3(\Z_2)$ se vyskytují právě tyto řády prvků: $1$, $2$, $3$, $4$, $7$.
Nápověda k (a)
Body Fanovy roviny můžeme nabijektit na nenulové body $\Z_2^3$. Zkuste vhodně intepretovat, co za podmnožiny tohoto prostoru jsou Fanovské přímky, aby $\G$ působilo na bodech Fanovy roviny podobně, jako matice působí na $\Z_2^3$.
Nápověda k (b)
Záleží, jaký máte konkrétně isomorfismus. Každopádně isomorfismus posílá množiny generátorů na množiny generátorů.
Nápověda k (c)
Buď můžeme použít naprosto standardní výpočet pro $\GL_3(\Z_2)$ (v podstatě jde o počet uspořádaných bází $\Z_2^3$), nebo si můžeme rozmyslet v $\G$, kam můžeme poslat $A$, kam pak $B$ a kam nakonec $C$.
Nápověda k (d)
Primárním omezením je Lagrange; dále je vhodné si uvědomit, že $\GL_3(\Z_2) \cong \G$ lze chápat jako podgrupu $\S_7$ (dokonce $\A_7$ podle (b)). Existence prvků prvočíselných řádů, které dělí řád grupy, plyne z obecné teorie. Prvek řádu $4$ se prostě najde, může pomoct např. Jordanův tvar. Kdyby existoval prvek řádu $6$, rozmyslete si, jak by mohla vypadat příslušná permutace a jak její druhá mocnina.
Řešení (a)
Sestrojíme bijekci mezi body Fanovy roviny a nenulovými body $\Z_2^3$ následovně: $A$, $B$, $C$ pošleme na vektory kanonické báze, $E$, $F$, $G$ vždy na součet obrazů krajních bodů příslušné strany trojúhelníka a $D$ na $(1, 1, 1)^T$. To proto, že Fanovské přímky pak odpovídají dvoudimenzionálním podprostorům $\Z_2^3$. Je lehké nahlédnout, že zobrazení vektorových prostorů nad $\Z_2$ je lineární a regulární právě tehdy, když pošle nulu na nulu a dvoudimenzionální podprostor na dvoudimenzionální podprostor.
Řešení (b)
Záleží, jaký máte konkrétně isomorfismus, v tom mém to jsou prohození nějakých dvou bodů na „straně trojúhelníka“ a příslušné prohození zbytku bodů, aby to vyšlo. Tyto permutace musí generovat $\G$, jelikož isomorfismus posílá množiny generátorů na množiny generátorů, a jsou sudé, takže všechny permutace v $\G$ budou sudé.
Řešení (c)
Je to $(2^3-2^0)(2^3-2^1)(2^3-2^2) = 168 = 2^3 \cdot 3 \cdot 7$.
Řešení (d)
Řád $1$ má identita, existence prvků řádu $2$, $3$, $7$ plyne z Cauchyho věty. Jelikož se pohybujeme v podgrupě $\A_7$, můžeme dostat jen tam vyskytující se řády, což spolu s Lagrangem omezí zbývající možnosti na řády na $4$ a $6$. Řád $4$ má například matice
\[ \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix}, \]
jak se snadno nahlédne „binomickou větou pro Jordanův tvar“. Kdyby existoval prvek řádu $6$, pak by musel (jakožto prvek $\A_7$) sestávat z trojcyklu a dvou dvojcyklů. Druhá mocnina takového prvku by tedy musela být samotný trojcyklus, takové se ale v $\G$ nevyskytují: nemůžeme ho provést s třemi body na fanovské přímce (zbytek se rozbije), stejně tak to nemůžeme provést s třemi nekolineárními body $X_1$, $X_2$, $X_3$, protože je-li $Y$ třetí bod na přímce $X_1X_2$, pak po provedení trojcyklu zjistíme, že by musel ležet i na $X_2X_3$, což není pravda.
Lineárně-algebraický argument neexistence prvku řádu 6
Kdyby matice $A \in \GL_3(\Z_2)$ splňovala $A^6 = E$, potom toto musí splňovat i všechna její vlastní čísla. Nad $\Z_2$ se polynom $x^6 + 1$ rozkládá jako $(x+1)^2(x^2+x+1)^2$, což vidíme, že se rozkládá na kořenové činitele ve čtyřprvkovém tělese $\Z_2[\alpha]/(\alpha^2 + \alpha + 1)$. Pokud by $A$ měla za vlastní číslo jen $1$, pak rozborem možných Jordanových tvarů vidíme, že by mohla mít jen řády $1$, $2$ nebo $4$. Pokud ovšem má za vlastní číslo $\alpha$, tak musí mít za vlastní číslo i $\alpha+1$, a to ve stejné násobnosti (a naopak; je to stejný argument jako u komplexních vlastních čísel reálných matic). Jediným možným Jordanovým tvarem je tedy diagonální matice, která má na diagonále (v nějakém pořadí) $\alpha$, $\alpha+1$ a $1$, ale ta má zřejmě řád jen $3$.
Nechť $\G$ je grupa, $\NN$ její normální podgrupa a $\varphi \colon \G \to \S(X)$ akce $\G$ na nějaké množině $X$.
- Nahlédněte, že $\varphi$ lze zúžit na akci $\NN$ na $X$.
- Nechť $Y$ je množina orbit oné akce $\NN$ na $X$ z předchozího bodu. Nahlédněte, že $\G/\NN$ „přirozeně“ působí na množině $Y$.
- Řekněme (nebo připomeňme), že akce je věrná, pokud je příslušný grupový homomorfismus prostý. Ukažte na příkladu, že i když byla původní akce věrná, nemusí být tato nová akce věrná.
Nápověda k (c)
Třeba by to mohlo fungovat u $\G = \S_3$ a $\NN = \A_3$. Dá se vyrobit i situace, kdy akce $\NN$ bude mít jedinou orbitu (tím to bude určitě vyřízeno).
Řešení (b)
Definujeme působení $\G/\NN$ na $Y$ takto: pro $g \in G$ a (orbitu) $O \in Y$ bude $gN(O) = gO$ (na všechny prvky $O$ zapůsobíme akcí $g$ a dostaneme novou množinu). Toto je dobře definované: je-li $g_1N = g_2N$, pak $g_1 = g_2 n$ pro nějaké $n \in N$, ovšem $n O = O$, jelikož $O$ je orbita akce $\NN$. Navíc $gO$ je opět prvek $Y$, neboli orbita akce $\NN$: mějme totiž dva prvky $gO$, nějaké $g(x)$ a $g(y)$ pro $x, y \in O$. Pak, protože je $O$ orbita, máme $y = n(x)$ pro nějaké $n \in N$. Pak $g(y) = (gn)(x)$ a jelikož je $\NN$ normální, existuje $n' \in N$ takové, že $n'g = gn$ (konkrétně je $n' = gng^{-1}$), takže $g(y) = n'(g(x))$, neboli z každého prvku $gO$ se dostanu do každého akcí $\NN$; podobně (s využitím normality) se ukáže, že $gO$ je i uzavřená na akci prvky $\NN$. Dále platí $(gN)(hN)(O) = (ghN)(O)$ z toho důvodu, že prvky $N$ jen zpermutují své orbity. Konečně $1N(O) = O$, takže jde o akci.
Řešení (c)
Funguje třeba množina všech trojic $0$ a $1$, na kterém $\S_3$ působí permutováním souřadnic (složek). Toto je určitě věrná akce: Trojcykly působí neidenticky na všech nekonstantních trojicích a transpozice působí neidenticky na těch trojicích, které mají na příslušných dvou souřadnicích různou hodnotu. Protože ale všechny trojice obsahují jednu hodnotu aspoň dvakrát, to, co dostaneme pomocí transpozic, dostaneme i pomocí trojcyklů (orbity jsou v obou případech prostě množiny těch trojic, které mají stejný počet jedniček, nebo stejný počet nul, chcete-li). Pokud bychom začali už např. s množinou všech trojic, které obsahují právě dvě jedničky, budou mít akce $\S_3$ i $\A_3$ pouhou jednu orbitu.
Nechť $\G$ je grupa všech symetrií krychle, která působí na vrcholech krychle zřejmým způsobem.
- Dokažte, že podgrupa $\NN$ generovaná středovou symetrií $s$ krychle je normální v $\G$. Co jsou orbity $\NN$?
- Skrze působení $\G/\NN$ na orbitách akce $\NN$ nahlédněte, že tato faktorgrupa je isomorfní grupě rotací krychle.
- Co by se pokazilo, kdybychom se místo vrcholů dívali na stěny krychle?
Řešení (a)
Ve skutečnosti ona středová symetrie komutuje se všemi prvky $\G$ (to je vlastně jediná možnost, jak docílit toho, aby dvouprvková podgrupa jí generovaná byla normální). To se dá nahlédnout různými způsoby. Buď jsme dobří geometričtí nahlížeči a jen to odkýveme, nebo si můžeme skrze (jistě věrnou) akci zmíněnou výše reprezentovat jako podgrupu permutační grupy. Nechť jsou protější vrcholy krychle očíslovány čísly $1, \dots, 8$ tak, že součet protějších vrcholů je $9$.
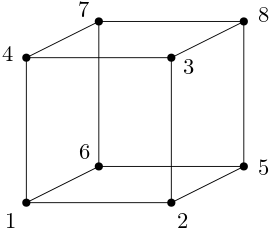
Pak ona středová symetrie je $(1\,8)(2\,7)(3\,6)(4\,5)$. Protože každou nepřímou symetrii dostaneme jako složení nějaké přímé s $s$, stačí ověřit komutování s přímými symetriemi, což jsou rotace podle nějakých os a jejich mocniny. Rotace podle osy stěny je vždy „správný“ čtyřcyklus, třeba jako $(1\,2\,3\,4)(5\,6\,7\,8)$, což s $s$ komutuje. Rotace kolem spojnice středů hran vždy sdílí s $s$ dvě transpozice a na zbývajících dvou má jen prohozené prvky (třeba $(1\,2)(7\,8)(3\,6)(4\,5)$), což opět s $s$ komutuje. Konečně rotace kolem tělesové úhlopříčky je složení dvou trojcyklů vrcholů, které jsou spojeny hranou s vrcholem oné úhlopříčky (např. $(2\,4\,6)(3\,5\,7)$), opět je snadno vidět, že takováto permutace komutuje s $s$, jelikož transpozice v $s$ jen přehazují čísla mezi trojcykly. Orbity akce $\NN$ jsou dvojice protějších vrcholů (přesně jak jsou uvedeny v cyklickém rozkladu $s$).
Asi lepší řešení (a)
To, že středová symetrie $s$ komutuje se všemi ostatními prvky, jak ukazujeme v předchozím bodě, začne být skutečně zřejmé ve chvíli, kdy si $\G$ nebudeme reprezentovat jako permutace, nýbrž jako matice působící na $\R^3$ (krychli umístíme do prostoru tak, že její vrcholy jsou $(\pm1, \pm1, \pm1)$). Ona středová symetrie pak totiž odpovídá mínus jednotkové matici – a ta zjevně komutuje dokonce se všemi prvky $\GL_3(\R)$, nejen symetriemi krychle.
Řešení (b)
$\G/\NN$ působí na dvojicích protějších vrcholů, jinak řečeno tělesových úhlopříčkách, takové působení nám už ale jednoznačně zadává rotaci (přímou symetrii) krychle.
Řešení (c)
Kdybychom se dívali na stěny, pak budou orbity dvojice protějších stěn. Ty ale nedokáží odlišit např. rotaci o $180^\circ$ podle osy stěny. Vůbec, do $\S_3$ těžko vnoříme tak velkou grupu, jako je grupa rotací krychle. Toto je další příklad na bod (c) z předchozí úlohy.
Uvažme těleso $\kk$ a $n$-dimenzionální aritmetický vektorový prostor $\kk^n$.
- Dokažte, že nenulové skalární násobky jednotkové matice tvoří normální podgrupu $\GL_n(\kk)$, kterou označíme $\NN_n(\kk)$ (nejde o standardní značení; ve skutečnosti tato podgrupa tvoří centrum).
- Co jsou orbity akce $\NN_n(\kk)$ při zúžení standardní akce $\GL_n(\kk)$ na $\kk^n$?
- ★ Položme $\PGL_n(\kk) = \GL_n(\kk)/\NN_n(\kk)$, to je tzv. projektivní grupa. Dokažte, že $\PGL_2(\kk)$ je isomorfní grupě „lineárních lomených funkcí“ tvaru
\[ \frac{ax + b}{cx + d}, \]
kde $a, b, c, d \in \kk$, $ad \neq bc$ a násobení je dáno skládáním funkcí (na nějaké definiční obory kašleme).
Řešení (a)
Skalární násobky identity se vším komutují, takže nepochybně jimi tvořená grupa bude normální.
Řešení (b)
Orbitou je jednak triviální vektor (jednoprvková orbita), jednak to jsou jednodimenzionální podprostory $\kk^n$, ze kterých vyjmeme triviální vektor.
Řešení (c)
Že je zobrazení
\[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \mapsto \frac{ax + b}{cx + d} \]
homomorfismus, se prostě ověří. Jeho jádrem jsou ty matice, které se zobrazí na identickou (lomenou) funkci $x/1$, což jsou přesně skalární násobky jednotkové matice. První věta o isomorfismu dává výsledek.

